 |
Предварительные вычисления для исследования
|
|
|
|
Исследование ряда погрешностей на соответствие нормальному закону распределения
Теоретические основы выполнения исследований
Обработка результатов измерений имеет место всегда, когда одна из определяемых величин получена несколько раз с отличными друг от друга значениями. При этом корректная оценка полученных результатов возможна, только если известны правила, определяющие поведение погрешностей измерений ∆. К главным таким правилам относят законы поведения погрешностей в дифференциальной F(∆) и интегральной F (∆) формах, их основные численные характеристики и представления законов в виде графического материала. Интегральная форма называется функцией распределения погрешностей 
, дифференциальная форма - функцией плотности распределения погрешностей . К основным характеристикам законов относят наиболее вероятное значение определяемой величины, называемое математическим ожиданием и обозначаемое МО (∆) или М(∆), или Е(∆); меру рассеивания измерений вокруг математического ожидания, называемую дисперсией и D(∆) (чаще используют просто величину σ(∆), называемую стандартом, так как он не имеет квадратичной размерности как у дисперсии). К дополнительным характеристикам законов относят меру скошенности относительно вертикальной оси симметрии, называемую асимметрией и обозначаемую А или 
и меру крутости, называемую эксцессом и обозначаемую Е.
Множество теоретических и практических исследований показывают, что результаты геодезических измерений подчиняются нормальному закону распределения (закону Гаусса) и имеют вид
В процессе измерений часто имеет место наличие грубых погрешностей (погрешностей, больших заданного допуска) или промахов (т.е. очень сильно отличающихся от других). С другой стороны, при наблюдениях в результатах могут содержаться и какие-либо постоянные составляющие, называемые систематическими ошибками.
|
|
|
Предварительные вычисления для исследования
В предварительных вычислениях ряд исследуется на наличие значимых систематических и грубых погрешностей а также меры однородности результатов по точности на основе каких-либо критериев.
Определение значимости систематического влияния. Следует иметь ввиду, что систематические влияния в рядах присутствуют всегда, но они могут быть значимы и не значимы. При определении наличия значимых систематических погрешностей в ряде имеют место два случая:
1) известно истинное значение определяемой величины Хист и произведено ее измерений х. В этом случае пользуются зависимостью
Где ∆=X- 
= 
- средняя квадратическая погрешность среднего арифметического, m-СКП одной величины, n - число элементов в ряде. Величина 
(квантиль t-распределения Стьюдента) определяется по уровню значимости q (или вероятности р) и числу избыточных измерений (числу степеней свободы) k = n - 1 и выбирается из статистических таблиц, или получается из какого либо программного продукта. Если неравенство (2) выполняется, то с вероятностью р = 1 - q считаем, что значимые систематические погрешности в ряде измерений отсутствуют.
| Аббе | 
| 
| 
| 
| 
| 
| 
|
| 1 | -0,06 | -0,04 | 0,00 | 0,00 | 0,00 | -1,96 | 3,84 |
| 2 | -2,02 | -1,99 | 3,98 | -7,94 | 15,83 | 1,04 | 1,08 |
| 3 | -0,98 | -0,95 | 0,91 | -0,87 | 0,83 | 1,59 | 2,54 |
| 4 | 0,61 | 0,64 | 0,41 | 0,26 | 0,17 | -0,67 | 0,45 |
| 5 | -0,05 | -0,03 | 0,00 | 0,00 | 0,00 | -1,06 | 1,13 |
| 6 | -1,12 | -1,09 | 1,19 | -1,30 | 1,42 | 0,49 | 0,24 |
| 7 | -0,63 | -0,60 | 0,36 | -0,21 | 0,13 | 0,88 | 0,77 |
| 8 | 0,25 | 0,28 | 0,08 | 0,02 | 0,01 | -1,24 | 1,54 |
| 9 | -0,99 | -0,97 | 0,93 | -0,90 | 0,87 | 1,97 | 3,87 |
| 10 | 0,98 | 1,00 | 1,00 | 1,01 | 1,01 | -1,62 | 2,61 |
| 11 | -0,64 | -0,61 | 0,38 | -0,23 | 0,14 | 2,45 | 6,00 |
| 12 | 1,81 | 1,84 | 3,37 | 6,19 | 11,37 | -2,89 | 8,35 |
| 13 | -1,08 | -1,05 | 1,11 | -1,17 | 1,23 | 1,28 | 1,64 |
| 14 | 0,20 | 0,23 | 0,05 | 0,01 | 0,00 | -1,72 | 2,96 |
| 15 | -1,52 | -1,49 | 2,23 | -3,33 | 4,98 | 0,80 | 0,64 |
| 16 | -0,72 | -0,70 | 0,48 | -0,34 | 0,23 | 0,13 | 0,02 |
| 17 | -0,59 | -0,57 | 0,32 | -0,18 | 0,10 | 0,99 | 0,99 |
| 18 | 0,40 | 0,43 | 0,18 | 0,08 | 0,03 | 0,54 | 0,29 |
| 19 | 0,94 | 0,97 | 0,94 | 0,91 | 0,88 | -0,64 | 0,41 |
| 20 | 0,30 | 0,33 | 0,11 | 0,04 | 0,01 | -0,67 | 0,45 |
| 21 | -0,37 | -0,35 | 0,12 | -0,04 | 0,01 | 1,19 | 1,41 |
| 22 | 0,82 | 0,84 | 0,71 | 0,60 | 0,50 | -0,02 | 0,00 |
| 23 | 0,80 | 0,83 | 0,68 | 0,56 | 0,47 | -0,68 | 0,46 |
| 24 | 0,12 | 0,15 | 0,02 | 0,00 | 0,00 | 0,45 | 0,20 |
| 25 | 0,57 | 0,60 | 0,36 | 0,21 | 0,13 | -0,16 | 0,03 |
| 26 | 0,41 | 0,44 | 0,19 | 0,09 | 0,04 | -1,40 | 1,96 |
| 27 | -0,99 | -0,96 | 0,92 | -0,88 | 0,85 | 1,75 | 3,05 |
| 28 | 0,76 | 0,79 | 0,62 | 0,49 | 0,38 | -1,42 | 2,01 |
| 29 | -0,66 | -0,63 | 0,40 | -0,25 | 0,16 | 0,05 | 0,00 |
| 30 | -0,60 | -0,58 | 0,33 | -0,19 | 0,11 | 0,78 | 0,61 |
| 31 | 0,18 | 0,20 | 0,04 | 0,01 | 0,00 | -0,48 | 0,23 |
| 32 | -0,31 | -0,28 | 0,08 | -0,02 | 0,01 | 0,18 | 0,03 |
| 33 | -0,13 | -0,10 | 0,01 | 0,00 | 0,00 | 0,73 | 0,53 |
| 34 | 0,60 | 0,62 | 0,39 | 0,24 | 0,15 | 0,45 | 0,20 |
| 35 | 1,05 | 1,07 | 1,15 | 1,24 | 1,33 | -1,24 | 1,55 |
| 36 | -0,20 | -0,17 | 0,03 | 0,00 | 0,00 | 0,53 | 0,28 |
| 37 | 0,33 | 0,36 | 0,13 | 0,04 | 0,02 | -0,57 | 0,32 |
| 38 | -0,24 | -0,21 | 0,04 | -0,01 | 0,00 | 0,47 | 0,22 |
| 39 | 0,23 | 0,26 | 0,07 | 0,02 | 0,00 | 0,21 | 0,04 |
| 40 | 0,44 | 0,47 | 0,22 | 0,10 | 0,05 | -1,06 | 1,12 |
| 41 | -0,62 | -0,59 | 0,35 | -0,20 | 0,12 | 0,89 | 0,80 |
| 42 | 0,27 | 0,30 | 0,09 | 0,03 | 0,01 | 0,33 | 0,11 |
| 43 | 0,60 | 0,63 | 0,39 | 0,25 | 0,16 | -0,51 | 0,26 |
| 44 | 0,09 | 0,12 | 0,01 | 0,00 | 0,00 | 1,64 | 2,68 |
| 45 | 1,73 | 1,76 | 3,09 | 5,43 | 9,53 | -2,34 | 5,47 |
| 46 | -0,61 | -0,58 | 0,34 | -0,20 | 0,11 | -0,13 | 0,02 |
| 47 | -0,74 | -0,71 | 0,50 | -0,36 | 0,25 | -1,01 | 1,03 |
| 48 | -1,75 | -1,72 | 2,97 | -5,11 | 8,80 | 2,66 | 7,08 |
| 49 | 0,91 | 0,94 | 0,88 | 0,82 | 0,77 | -0,04 | 0,00 |
| 50 | 0,87 | 0,89 | 0,80 | 0,72 | 0,64 |
|
|
|
2) Исследование на наличие существенного систематического влияния по критерию Аббе. Истинное значение величины не известно. Тогда наличие в результатах наблюдений постоянной составляющей может быть выяснено по наиболее распространенному в геодезии критерию Аббе [2 и др.]. Для этого выдвигаем гипотезу, что с вероятностью β в предложенном ряде отсутствует значимое систематическое влияние. По исследуемым величинам получаем практическую величину
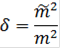
являющуюся отношением двух оценок дисперсий, средние квадратические ошибки которых получены как
где 
уклонение i - той величины от среднего
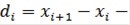
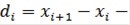последовательные разности
Для сравнения, по заданной вероятности β (или уровню значимости q), числу степеней свободы п и с использованием статистических таблиц критерия Аббе получают контрольную величину 
. Тогда, при δ > принимается гипотеза об отсутствии систематической ошибки с вероятностью β =1 - q. В противном случае (δ < ) следует принять гипотезу о постоянной составляющей в статистической совокупности и для корректной оценки исследуемых параметров ее необходимо исключить из ряда измерений. Для этого получают усредненную величину систематического влияния, равную среднему арифметическому из всех элементов, которую и исключаем из измерений, получая новый ряд 
с уменьшенной по сравнению с исходным рядом систематической составляющей
|
|
|
По исследуемым величинам получаю практическую величину:
где
| 
|
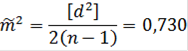
Проверим неравенство 
(
Неравенство не выполняется 
, значит модно утверждать, что в исследуемом ряде отсутствуют существенные систематические ошибки с вероятностью 
.
) Исследование ряда данных на наличие грубых ошибок по критерию Граббса. ( В зависимости от требований задачи существует масса критериев, решающих поставленную задачу: критерий Граббса, Диксона, Шарлье, Шовенэ и др. В работе для выявления грубых погрешностей предлагается использовать критерий Граббса. Критерий дает вероятность выполнения выдвинутой гипотезы о том, что максимальное, или минимальное значение из ряда не являются грубыми погрешностями. Для этого по экстремальным значениям выборки Хтах и Xmin, среднему арифметическому 
и средней квадратической погрешности т, вычисляют значения
Если Zвыч < zq, для максимального и минимального значения, то следует принять гипотезу об отсутствии в ряде грубых погрешностей, так как экстремальные значения не являются грубыми. Значения теоретической величины критерия zq получают по заданному аргументу q и числу элементов в выборке п по специальным статистическим таблицам критерия Граббса для zq. Если же zfвыч > zq, тогда или наибольшее или наименьшее значение ряда из дальнейшей обработки следует исключить.
Если не имеется таблиц статистики критерия Смирнова-Граббса, то её можно достаточно точно получить на основе формулы
где ta/ 2nn-2 - квантиль t-распределения Стьюдента с уровнем значимости а.
- 2 степенями свободы с п элементами в ряде.
|
|
|
Практические величины: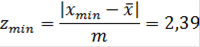 
| 
|
где 
, 
, 
Из статистических таблиц получим коэффициент 
для вероятности 
и степени свободы 
, равный 
. Проверяемое неравенство 
выполняется для максимального и минимального значений ошибки:
| 
|
Следовательно, можно утверждать, то с вероятностью 
ни левая, ни правая крайние в ряде ошибки не являются грубыми.
) Оценки основных характеристик ряда. Теоретическое значение математического ожидания для нормального закона распределения Гаусса равно нулю и, следовательно, если вычисленная его оценка 
M(X) будет отличаться от нуля на величину не более утроенной средней квадратической погрешности 
3 *m = ∆пред, то это говорит о том, что распределение исследуемых величин может быть близко к нормальному, но только по критерию близости теоретического значения математического ожидания к вычисленному значению. Оценки математического ожидания, дисперсии и стандарта получим по следующим формулам
Практические значения:
• среднее арифметическое 
;
• средняя квадратическая ошибка 
;
• оценка дисперсии 
;
5) Приближенные методы исследования на соответствие нормальному закону. Приближенные критерии исследования ряда погрешностей на соответствие нормальному закону распределения используют сравнение некоторых известных теоретических характеристик нормального закона и их вычисленного по результатам измерений аналога. Кроме наиболее распространенной средней квадратической погрешности т используют средние абсолютные v и вероятные (срединные) ошибки r. Между тремя ошибками т, V и r для нормального закона распределения величин имеются теоретически строгие соотношения
«Критерий ничтожных влияний», гласящий, что величина считается неизменной, если её вариация составляет не более 11% от самой величины.
Для вычисления средней абсолютной ошибки пользуются формулами:
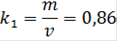
Приближённые критерии на основе коэффициентов
 =0,86 (при теоретическом значении 1.25)
| |
 =0,77 (при теоретическом значении 1.48)
| |
 =0,90 (при теоретическом значении 1.18)
|
Не все абсолютные отклонения между практическими и теоретическими значениями величин меньше допустимых по критерию ничтожных погрешностей 0,393 
0. 138,0.712 
0. 163,0,284 0.130.
Характеристики будут такими:
| 
|
Проведём контроль:
Эксцесс - мера «крутости».
| 
|
Проведем контроль:
| 
|
Это говорит о том, что эмпирическое распределение по отношению к теоретическому на допустимую величину скошено вправо (отрицательное) и на допустимую величину выше нормального (положительное).
|
|
|
6-8) Графический критерий исследования ряда погрешностей на соответствие нормальному закону распределения
Для дальнейших исследований погрешностей на соответствие их нормальному закону распределения строят для ряда одно из его графических представлений, например, в виде гистограммы или многоугольника распределения, с нанесенной поверх её теоретической кривой закона Гаусса с параметрами О и m, называемой огивой. В данной работе предлагается использовать гистограмму. Построение гистограммы начинают с разбиения ряда погрешностей на интервалы. Число интервалов к зависит от точности измерений, количества элементов в выборке и является в некотором смысле произвольным. Основное требование к количеству и величине интервалов заключается в том, чтобы полученный на их основе график был наглядным и правдоподобным. Длину интервала Q можно получить, например, используя следующие формулы
если известно число интервалов к, и
В геодезии чаще всего в такого рода исследованиях ряд делят на 12 интервалов, каждый из которых должен быть в 0.5 m.
Далее необходимо подсчитать число n. элементов ряда, принадлежащих j-му интервалу, и вычислить практические оценки неизвестных вероятностей (частоты 
) по формуле
Вертикальные составляющие гистограммы, называемые высотами прямоугольников
На этом же графике необходимо построить теоретическую кривую, соответствующую нормальному закону, которая наилучшим образом сглаживает данное эмпирическое статистическое распределение. Кривая строится на основе формулы плотности вероятности для закона Гаусса
Наиболее точный критерий соответствия исследуемого ряда нормальному закону распределения получу, используя критерий χ2 Пирсона по формулам:
Здесь 
- теоретическая вероятность попаданияслучайной величины в соответствующий интервал.
Таблица построения гистограммы эмпирического закона распределения
| Интервал в долях | Интервал в секундах | Количество элементов в интервале | Относит. частота | Высота прямоугольника |
| m(t) | (Ø) | 
| 
| 
|
| -3m | -2,50 | 0 | 0 | 0 |
| -2,5m | -2,08 | 3 | 0,06 | 0,1441 |
| -2m | -1,67 | 3 | 0,06 | 0,1441 |
| -1,5m | -1,25 | 6 | 0,12 | 0,2882 |
| -1m | -0,83 | 5 | 0,1 | 0,2402 |
| -0,5m | -0,42 | 7 | 0,14 | 0,3363 |
| 0m | 0,00 | 7 | 0,14 | 0,3363 |
| 0,5m | 0,42 | 6 | 0,12 | 0,2882 |
| 1m | 0,83 | 4 | 0,08 | 0,1921 |
| 1,5m | 1,25 | 1 | 0,02 | 0,0480 |
| 2m | 1,67 | 2 | 0,04 | 0,0961 |
| 2,5m | 2,08 | 1 | 0,02 | 0,0480 |
| 45 | 0,9 |
При этом сумма элементов по интервалам должна равняться общему количеству элементов в ряде; сумма частот равняется единице в пределах ошибки округления; сумма высот прямоугольников равняется 2/т. Выбрав масштабы по горизонтальной оси для величин интервалов (например, 0.5т - 1 см), по вертикальной для высот прямоугольников (например, 0.05 от - высоты прямоугольника - 1 см), откладывают по соответствующим границам вертикальные высоты, которые замыкаются в прямоугольники. Полученный график и будет называться гистограммой (эмпирическим представлением плотности закона распределения), площадь которого равна единице
) На этом же графике необходимо построить теоретическую кривую, соответствующую нормальному закону, которая наилучшим образом сглаживает (выравнивает) данное эмпирическое статистическое распределение. Кривая строится на основе формулы плотности вероятности для закона Гаусса
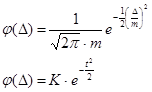
Обычно величина t изменяется от -3 до 3 через 0.5, так что вычисления не представляют трудности. Необходимо учитывать, что функция симметричная, т.е. f(x)= - f(x) Значения функции с m = 1 приведены в любых книгах по статистике или обработке измерений в виде таблиц и также могут быть использованы при вычислениях.
Значения теоретической функции плотности на границах интервалов будут равны:
| t = | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| φ(∆)= | 0,48 | 0,42 | 0,29 | 0,16 | 0,06 | 0,02 | 0,01 |
По вычисленным данным строят график на гистограмме
10) Наиболее точный критерий соответствия исследуемого ряда нормальному закону распределения получим используя критерий 
-Пирсона.
Следует иметь в виду, что все критерии соответствия являются частными случаями общего алгоритма статистической проверки гипотез, в основе которой лежат следующие пункты:
) выдвижение с доверительной вероятностью исходной гипотезы;
) получение теоретического значения критерия;
) сравнение двух значений критериев и вывод.
Предположим, что с вероятностью 
ряд ошибок распределен нормально. Из статистических таблиц распределения -Пирсона по числу степеней свободы 
находим эталонное значение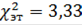 
.
| i | Интервалы  в долях m    n  
| |||||
| 1 2 3 4 5 6 7 8 9 10 11 12 13 | -3 -2.5 -2.5 -2.0 | 0.0013 0.0062 | 0.0049 0.0165 | 0 3 | 0.25 0.85 | -0.25 2.15 |
| -2.0 -1.5 -1.5 -1.0 -1.0 -0.5 -0.5 0 0 0.5 0.5 1.0 1.0 1.5 1.5 2.0 2.0 2.5 2.5 3.0 3.0 | 0.0228 0.0668 0.1587 0.3085 0.5000 0.6915 0.8413 0.9332 0.9772 0.9938 0.9987 | 0.0441 0.0918 0.1499 0.1915 0.1915 0.1499 0.0918 0.0441 0.0165 0.0049 | 3 6 5 7 7 6 4 1 2 1 | 2.2 4.6 7.45 9.6 9.6 7.46 4.6 2.2 0.85 0.25 | 0.8 1.4 -2.45 -2.6 -2.6 -1.45 -0.6 -1.2 1.15 0.75 | |
| ∑ | 0.998 | 45 | 49.9 |
На основании проведенных исследований установлено, что рад является случайным, оценка математического ожидания в виде среднего арифметического не превосходит утроенной средней квадратической ошибки, то есть практически равна нулю. Количество положительных элементов (23) равно количеству отрицательных (27).
В результате вычисления критерия Аббе и сравнения практических и теоретических значений выявлено, что в ряду отсутствуют значимые систематические влияния с вероятностью 
и с этой же вероятностью крайние значения вариационного ряда не являются грубыми.
Приближённые критерии соответствия нормальному закону, учитывающие расхождения между теоретическими и практическими значениями соотношениями между тремя видами ошибок: средней квадратической, средней абсолютной и вероятной, показывают, что ряд соответствует нормальному закону. Значениями асимметрии и эксцесса можно пренебречь.
Визуальный анализ гистограммы (эмпирическое распределение) и огивы (вид теоретического закона распределения) показывает недостаточное согласование по форме и величине между ними, что говорит о недостаточном соответствии нормальному закону распределения.
Наиболее точные результаты соответствия исследуемого ряда нормальному закону дает критерий c2 Пирсона, который учитывает расхождение между практическими и теоретическими частотами по всем выделенным интервалам.
Таким образом, выполненные исследования ряда ошибок на соответствие нормальному закону распределения дают по всем использованным критериям положительные результаты, что позволяет сделать вывод о достаточной близости ряда предполагаемому закону. И сделать вывод, что мой ряд достаточно хорошо подчиняется нормальному закону распределения.
погрешность распределение закон статистический
|
|
|
