 |
Совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ)
|
|
|
|
Формулировки логических законов
1. Закон двойного отрицания:
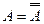 .
.
Двойное отрицание исключает отрицание.
2. Переместительный (коммутативный) закон:
• для логического сложения:
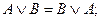
• для логического умножения:
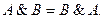
Результат операции над высказываниями не зависит от того,
в каком порядке берутся эти высказывания. В обычной алгебре
а + b = b + а, а × b = b × а.
3. Сочетательный (ассоциативный) закон:
• для логического сложения:

• для логического умножения:

При одинаковых знаках скобки можно ставить произвольно или вообще опускать. В обычной алгебре
(А + B) + С = А + (B + С) = А + B + С,
А × (B × С) = А × (B × С) = А × B × С.
4. Распределительный (дистрибутивный) закон:
• для логического сложения:

• для логического умножения:
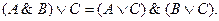
Закон определяет правило выноса общего высказывания за скобку.
В обычной алгебре  .
.
5. Закон общей инверсии (законы де Моргана):
• для логического сложения:

 ;
;
• для логического умножения:
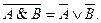
6. Закон идемпотентности (от латинских слов idem — «тот же самый» и potens — «сильный»; дословно — «равносильный»):
• для логического сложения:
 Ú
Ú 
• для логического умножения:
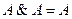 .
.
Закон означает отсутствие показателей степени
7. Законы исключения констант:
• для логического сложения:
 Ú
Ú 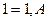 Ú
Ú 
• для логического умножения:
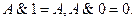
8. Закон противоречия:
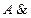

Невозможно, чтобы противоречивые высказывания были одновременно истинными.
9. Закон исключения третьего:
 Ú
Ú 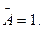
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
10. Закон поглощения:
• для логического сложения:
 Ú
Ú 
• для логического умножения:
 Ú
Ú 
11. Закон исключения (склеивания):
|
|
|
• для логического сложения:
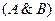 Ú
Ú 
• для логического умножения:
 Ú
Ú 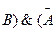 Ú
Ú 
12. Закон контрапозиции (правило перевертывания):
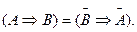
Переместительный, сочетательный (для логических сложения и умножения) и распределительный (для логического сложения) законы имеют полную аналогию с обычной алгеброй. Для других законов такой аналогии нет.
Доказательство логических законов
Справедливость приведенных законов можно доказать табличным способом: надо выписать все наборы значений А и В, вычислить для них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.
Пример. Докажем справедливость закона инверсии для логического сложения:

| A | B | AÚB | 
| 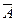
| 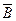
| 
|
Совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ)
Если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией, то такая форма представления называется нормальной.
Элементарная конъюнкция — конъюнкция конечного множества логических переменных и их инверсий.
Элементарная дизъюнкция — дизъюнкция конечного множества логических переменных и их инверсий.
Число аргументов, образующих элементарную дизъюнкцию или конъюнкцию, называется ее рангом.
Пример 1. Х & Y & Z, Х &. Y & Z — элементарные конъюнкции третьего ранга. Х v Y, Х v Y — элементарные дизъюнкции второго ранга.
Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операцией дизъюнкции.
Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции, связанные между собой операцией конъюнкции.
Одну и ту же логическую функцию можно представить разными ДНФ и КНФ.
Пример 2. Нетрудно убедиться (построив таблицы истинности для каждой из логических формул или проведя преобразования на основании логических законов), что приведенные ниже формулы определяют одну и ту же логическую функцию F(X, Y, Z):
|
|
|
1) 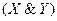 Ú
Ú  Ú
Ú  ;
;
2) 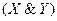 Ú
Ú 
 Ú
Ú  .
.
Для исключения неоднозначности записи логические функции могут быть представлены в совершенных дизъюнктивной и конъюнктивной нормальных формах.
Совершенная дизъюнктивная нормальная форма (СДНФ) отвечает следующим требованиям:
1) в ней нет двух одинаковых элементарных конъюнкций;
2) ни одна элементарная конъюнкция не содержит двух одинаковых переменных;
3) ни одна элементарная конъюнкция не содержит переменную вместе с ее инверсией;
4) все конъюнкции имеют один и тот же ранг.
Аналогичным требованиям подчиняется и совершенная конъюнктивная нормальная форма (СКНФ).
Пример 3. Если логическая функция содержит конъюнкции разных рангов, то для получения СДНФ следует повысить ранг младших конъюнкций, используя закон исключения третьего.
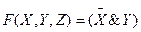 Ú
Ú 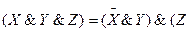 Ú
Ú  Ú
Ú 
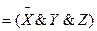 Ú
Ú  Ú
Ú  .
.
СДНФ и СКНФ можно получить по табличному представлению логической функции.
Алгоритм образования СДНФ по таблице истинности
1. Выделить в таблице истинности все наборы переменных, на которых функция принимает единичные значения.
2. Для каждого выбранного набора записать элементарные конъюнкции, содержащие без инверсии переменные, принимающие в соответствующем наборе значение 1 и с инверсией —
переменные, принимающие значение 0.
3. Соединить элементарные конъюнкции знаком дизъюнкции.
|
|
|


