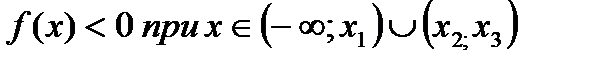|
Основные теоремы о пределах
|
|
|
|
Государственное образовательное учреждение
Среднего профессионального образования
МАТЕМАТИКА
Методическое пособие
для студентов заочной формы обучения
по специальностям
Методическое пособие предназначено для студентов – заочников, обучающихся по специальностям В пособии по каждой теме дисциплины содержится краткий теоретический материал, образцы решения и оформления примеров, литература, необходимая при изучении материала, а также вопросы для самопроверки.
Приведены задания обязательной контрольной работы по дисциплине «Математика».
Введение
Курс математики, который предстоит освоить студенту – заочнику, является фундаментом математического образования. Математические знания имеют важное значение для успешного изучения общетеоретических и специальных дисциплин, которые предусмотрены учебными планами различных специальностей.
По специальностям математика изучается в течении двух семестров. По результатам изучения дисциплины студенты должны выполнить две контрольные работы и сдать экзамен. В межсессионный период и во время сессий со студентами – заочниками проводятся лекционные и практические занятия, а также консультации.
В настоящем пособии содержатся общие рекомендации студентам – заочникам по работе над курсом математики, программа курса, методические указания по темам дисциплины с вопросами для самопроверки, решения типовых задач и задания контрольной работы №2.
Общие рекомендации по работе
над курсом математики
Формой обучения студента – заочника является самостоятельная работа над учебным материалом, которая состоит их следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных работ. В процессе самостоятельной работы студент может обращаться к преподавателю с вопросами для получения письменной или устной консультации. В помощь заочникам организуются чтение лекций, практические занятия. Завершающим этапом изучения отдельных частей курса математики является сдача семестрового экзамена в соответствии с учебным планом по специальности.
|
|
|
Изучение материала по учебнику
Изучение материала по учебнику следует выполнять согласно указанным в программе курса темам. Изучая тот или иной вопрос темы по учебнику, целесообразно выполнять на бумаге все вычисления и вычерчивать имеющиеся в учебнике чертежи.
При самостоятельном изучении материала полезно вести конспект. В конспект по мере проработки материала рекомендуется вписывать определения, теоремы, формулы, уравнения и т.п. Поля конспектов могут послужить для выделения тех вопросов, на которые необходимо получить письменную или устную консультации. Ведение конспекта должно быть аккуратным, расположение текста хорошо продуманным. Конспект поможет в подготовке к теоретической части экзамена.
Решение задач
Чтение учебника должно сопровождаться разбором предлагаемых решений задач. Решение рекомендуется выполнять в отдельной тетради.
Каждый этап решения задачи должен быть обоснован, исходя из теоретических положений курса. Решение задач и примеров следует излагать подробно, вычисления располагать в строгом порядке, отделяя вспомогательные вычисления от основных. Чертежи можно выполнять от руки, но аккуратно.
В промежуточные вычисления не следует вводить приближенные значения корней, числа p и других математических констант.
Самопроверка
Опыт прочного усвоения материала темы показывает, что самопроверку проводить необходимо. В настоящем пособии приводятся для самопроверки вопросы, которые акцентируют внимание на наиболее важных, ключевых положениях темы. В процессе выполнения самопроверки необходимо избегать пользования учебником или конспектом. Желание обратиться к учебнику или конспекту показывает недостаточное усвоение материала темы.
|
|
|
Консультации
При изучении теоретического материала или при решении задач у студента могут возникнуть вопросы, разрешить которые самостоятельно не удается. В такой ситуации студенту следует обратиться к преподавателю для получения от него письменной или устной консультации. При этом необходимо точно указать вопрос, учебник и место в учебнике, где рассмотрен затрудняющий студента вопрос. Если непреодолимые затруднения возникли при решении задачи, то следует указать характер затруднения, привести план решения.
Контрольная работа
В процессе изучения курса студент должен выполнить одну контрольную работу, которая проходит рецензирование. По полученным результатам студент может сделать выводы о степени усвоения им соответствующего раздела курса, внести коррективы в процесс последующей самостоятельной работы по изучению теоретического материала.
К выполнению контрольной работы следует приступать после тщательного разбора имеющихся в учебнике и сборниках задач решений с ответами. В дополнение к предложенным задачам сборников в данном пособии рассмотрены некоторые примеры.
Контрольные работы должны выполняться самостоятельно, так как в противном случае рецензирование работы как диалог общения преподавателя – рецензента и студента с целью оказания последнему методической помощи не достигнет цели.
Прорецензированные и зачтенные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять, поскольку без их предъявления студент не допускается к сдаче экзамена.
Лекции, практические занятия
Во время экзаменационных сессий для студентов - заочников читаются лекции, проводятся занятия. На лекциях и практических занятиях проводится обзор наиболее важных разделов курса, могут рассматриваться отдельные вопросы программы, отсутствующие или недостаточно полно освященные в рекомендуемых учебных пособиях.
|
|
|
Зачеты и экзамены
К зачету допускаются студенты, выполнившие контрольную работу (работы должны быть зачтены преподавателем-рецензентом). Экзамен проводится в письменной форме. Студенту предстоит ответить на вопросы экзаменационного билета. Как правило, экзаменационный билет содержит один теоретический вопрос и три практических задания. Определения, теоремы, правила должны формулироваться точно и с пониманием существа дела: решение задач должно выполняться без ошибок и уверенно. Только при выполнении этих условий знания студента могут быть признаны удовлетворяющими требованиям, предъявленными программой.
Программа дисциплины
«МАТЕМАТИКА»
Раздел I. Введение в математический
анализ
Тема 1: Множества. Переменные величины и функции
Числовые множества. Определение функции. Классификация функций. Область определения и область значения функций. Свойства функций: нули функции, четность, нечетность, периодичность, монотонность, точки локального экстремума, промежутки знакопостоянства.
Тема 2. Теория пределов
Предел функции в точке и на бесконечности. Основные теоремы о пределах: предел суммы и разности двух функций, предел произведения двух функций, предел отношения двух функций. Техника вычисления пределов.
Раздел II. Дифференциальное исчисление
Тема 3. Производная и дифференциал функции
Определение производной. Геометрический и механический смысл производной. Правила дифференцирования функции. Таблица производных. Производные от сложных функций. Дифференциал. Производные высших порядков.
Тема 4. Применение производной к исследованию функций
Условия возрастания и убывания функции. Точки экстремума функции. Выпуклость, вогнутость кривой, точки перегиба. Общая схема исследования функции и построения ее графика.
Раздел III. Интегральное исчисление
Тема 5. Неопределенный интеграл
Понятие первообразной. Свойства неопределенных интегралов. Таблица интегралов. Основные методы интегрирования: непосредственный метод, метод подстановки.
|
|
|
Тема 6: Определенный интеграл
Определение определенного интеграла, его геометрический смысл. Свойства определенного интеграла. Формула Ньютона – Лейбница. Основные методы вычисления определенного интеграла: непосредственный метод, метод замены переменных.
Литература
Основная
1. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие., М.: Наука. Гл. ред. физ. мат. литературы., 1990
2. Алгебра и начала анализа/ Под редакцией Г.Н.Яковлева., М.: Наука.: Наука. Гл. ред. физ. мат. литературы., 1981. – Ч.1,2.
3. Богомолов В.Н. Практические занятия по математике., М.: Высшая школа, 1982.
4. Шипачев В.С. Высшая математика., М.: Высшая школа., 1990.
5. Шипачев В.С. Задачник по высшей математике., М.: Высшая школа., 1998
6. Апанасов П.Т., Орлов М.И. Сборник задач по математике., М.: Высшая школа., 1987.
Дополнительная
7. Справочник по математике., М.: «Лист».,1999.
8. Математическая энциклопедия. М., 1977 – Т.1; 1979 – Ч.2.; 1983 Т.3.
9. Кудрявцев Л.Д. Краткий курс математического анализа. М.: Наука. Гл. ред. физ. мат. литературы., 1989.
Методические указания
Введение в математический анализ
Понятие функции, свойства функций
Определение: Пусть даны два числовых множества X и Y. Функцией называется правило, по которому каждой переменной 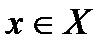 соответствует одно и только одно значение
соответствует одно и только одно значение  .
.
Функция обозначается 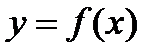 или
или 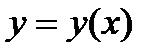 или
или
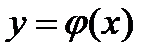 .
.
Переменная x – независимая переменная или аргумент функции; переменная y – зависимая переменная или значение функции.
Определение: Множество всех значений независимой переменной x, при которых функция существует называется областью определения функции и обозначается D(y).
Определение: Множество всех возможных значений зависимой переменной y называется областью значений функции и обозначается E(y).
Используют следующие способы задания функции:
1.Аналитический способ – задание функций с помощью формул. Например,
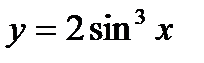 ,
, 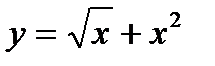 .
.
2.Графический способ – задание функций с помощью графика. Например,
| y x |
| y x |
3.Табличный способ – задание функций с помощью таблиц.
Например,
| x | -3 | -2 | -1 | |||
| y |
| t | ||||
| S |
Свойства функций приведены в таблице:
| Название свойства | Определение | Графическое изображение | |||
| Нули функции |
Нулём функции называется то значение х, при котором функция обращается в 0, то есть
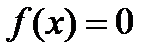 . .
|
Нули – это точки пересечения графика функции с осью Ох. | |||
| Четность функции |
Функция называется чётной, если для любого х из области определения выполняется равенство
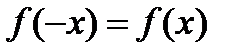
|
Четная функция симметрична относительно оси Оу | |||
| Нечет-ность функции |
Функция называется нечётной, если для любого х из области определения выполняется равенство
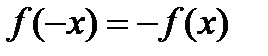 . .
|
Нечетная функция симметрична относительно начала координат. | |||
| Функция которая не является ни чётной,ни нечётной называется функцией общего вида. |
| ||||
| Возрас-тание функции | Функция 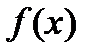 называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е. называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е.
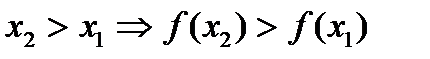
|
| |||
| Убывание функции |
Функция 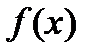 называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е. называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е.
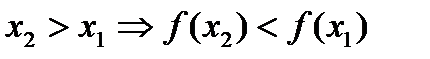
|
| |||
| Промежутки, на которых функция либо только убывает, либо только возрастает называются промежутками монотонности. |
| ||||
| Локаль-ный максимум |
Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство:
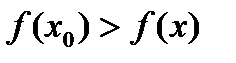 . .
|
| |||
| Локаль-ный минимум |
Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство:
 . .
|
| |||
| Точки локального максимума и точки локального минимума называются точками локального экстремума. |
| ||||
| Перио-дичность функции |
Функция f(x) называется периодичной, с периодом Т, если для любого х выполняется равенство
 . .
|
| |||
| Проме-жутки знакопос-тоянства | Промежутки, на которых функция либо только положительна, либо только отрицательна называются промежутками знакопостоянства. |
| |||
| Непре-рывность функции |
Функция 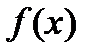 называется непрерывной в точке называется непрерывной в точке 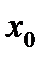 , если предел функции при , если предел функции при 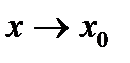 равен значению функции в этой точке, т.е. равен значению функции в этой точке, т.е.
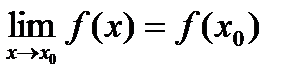 . .
|
| |||
| Точки разрыва | Точки, в которых нарушено условие непрерывности называются точками разрыва функции. |
| |||
Теория пределов
Определение: Число А называется пределом функции y=f(х) при х, стремящемсяк а, если для любой последовательности чисел х1, х2, х3, …,.хn ,… сходящейся к числу а, следует, что последовательность значений функции f(х1), f(х2),…, f(хn)… сходится к числу А.
Предел функции в точке а обозначается
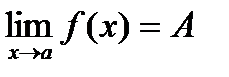 .
.
Основные теоремы о пределах
Приведем основные теоремы, на которых основано вычисление пределов:
1. 
2. 
3. 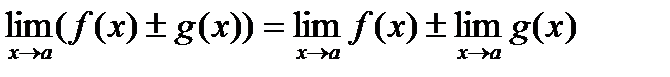
4. 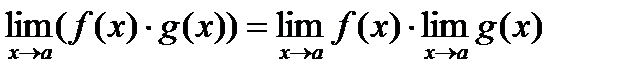
5. 
6. 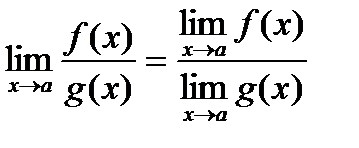
! Все правила имеют смысл, если пределы функций 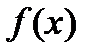 и
и  существуют.
существуют.
Техника вычисления пределов
При вычислении предела элементарной функции f(x) приходится сталкиваться с двумя существенно различными типами примеров.
· Функция f(x) определена в предельной точке x = a. Тогда
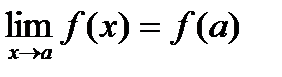 .
.
· Функция f(x) в предельной точке x = a не определена или же вычисляется предел функции при x→∞. Тогда вычисление предела требует в каждом случае индивидуального подхода.
Необходимо помнить, что
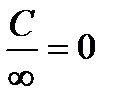 ,
, 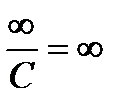 ,
,  ,
,  ,
, 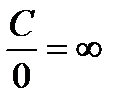 ,
, 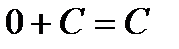 .
. 
Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке x = a или при x→∞ представляет собой неопределенность (типа 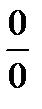 ,
,  ,
,  ,
, 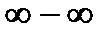 ,
, 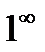 ,
,  ,
,  ).
).
При вычислении пределов при 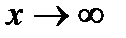 основные теоремы о пределах сохраняют силу и, кроме того, используются правила:
основные теоремы о пределах сохраняют силу и, кроме того, используются правила:
а) чтобы раскрыть неопределенность типа 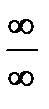 , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;
, необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;
б) чтобы раскрыть неопределенность типа 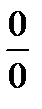 , необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной;
, необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной;
в) чтобы раскрыть неопределенность типа 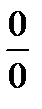 , иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности;
, иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности;
г) чтобы раскрыть неопределенность типа 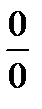 , зависящую от
, зависящую от
иррациональности, достаточно перевести иррациональность из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности;
д) чтобы раскрыть неопределенность типа  , необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида
, необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида  или
или 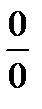 .
.
Рассмотрим некоторые примеры.
Вычислить пределы функций:
Пример 1: 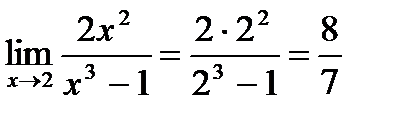
Пример 2: 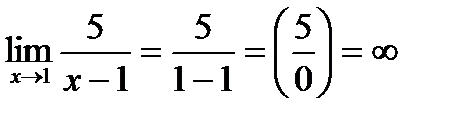
Пример 3: 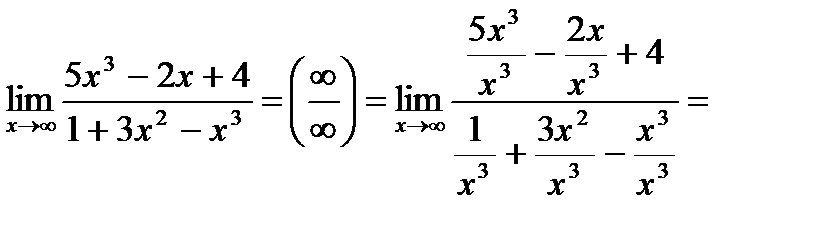
= 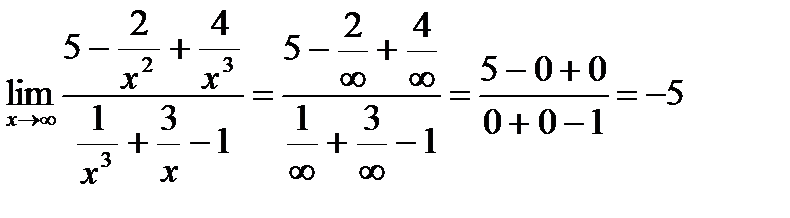
Пример 4: 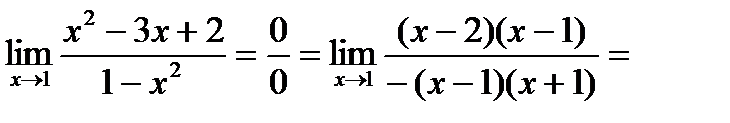

Пример5: 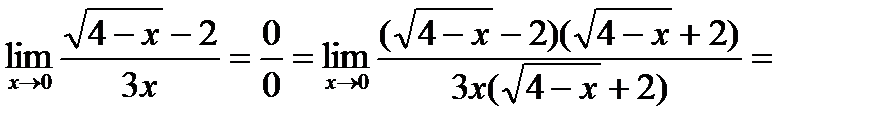
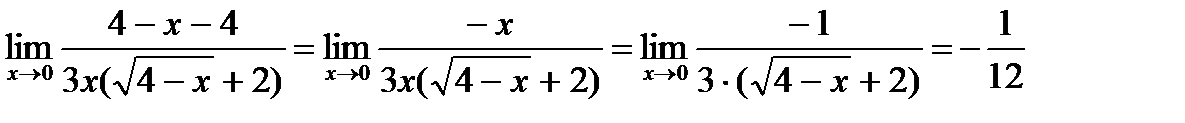
Вопросы для самопроверки:
1. Что называется функцией?
2. Что такое область определения и область значений функции
3. Перечислите способы задания функций, их достоинства.
4. Перечислите основные свойства функций.
5. Дайте определение предела функции в точке.
6. Какая функция называется непрерывной в точке?
7. Сформулируйте основные свойства пределов.
8. Как раскрывается неопределенность вида  ,
, 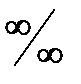 ?
?
Дифференциальное исчисление
Понятие производной
Определение: Производной функции 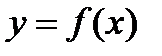 по аргументу x называется предел отношения ее приращения
по аргументу x называется предел отношения ее приращения 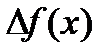 к приращению
к приращению 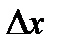 аргумента x, когда приращение аргумента стремится к нулю:
аргумента x, когда приращение аргумента стремится к нулю:
 .
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной: скорость есть первая производная пути по времени, т.е.  .
.
Геометрический смысл производной: тангенс угла наклона касательной к графику функции 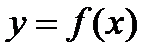 равен первой производной этой функции, вычисленной в точке касания, т.е.
равен первой производной этой функции, вычисленной в точке касания, т.е. 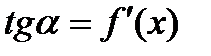
Уравнение касательнойк графику функции  в точке
в точке  :
:
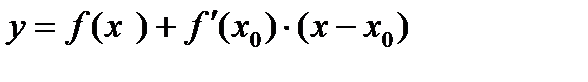
Уравнение нормали к графику функции  в точке
в точке  :
:
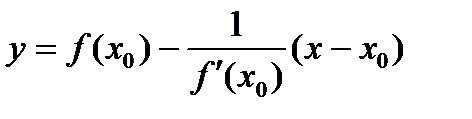
Таблица производных
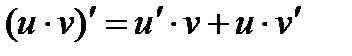
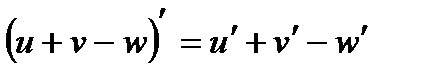
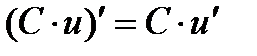

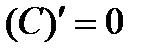
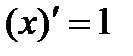

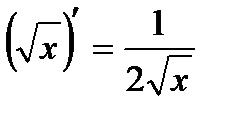

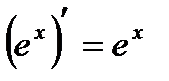
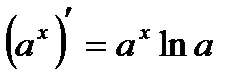
| 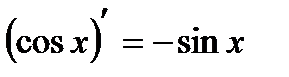
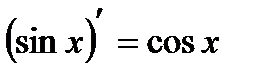
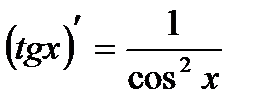
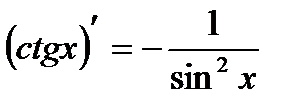
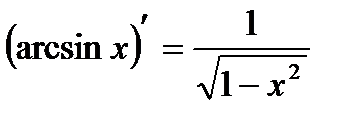
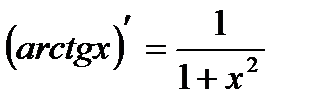
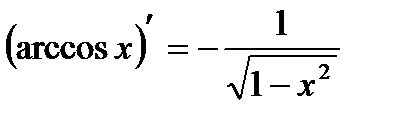
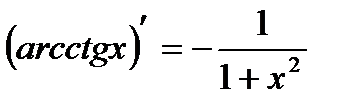

|
Процесс нахождения производных называется дифференцированием функции.
Рассмотрим примеры.
Найти производные функций:
Пример 1: 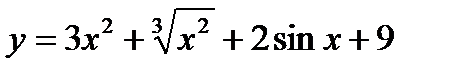
Решение: 
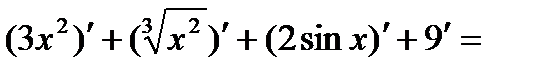

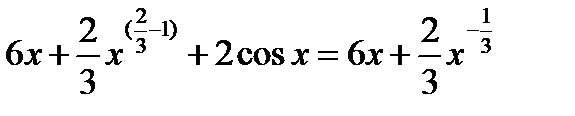 +
+


Пример2: 
Решение: 
Пример 3: 
Решение: 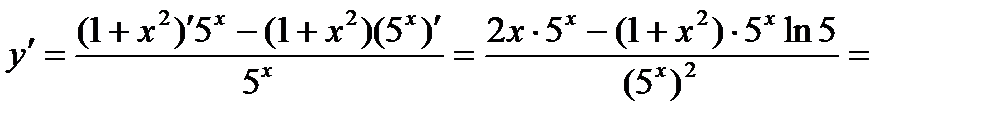
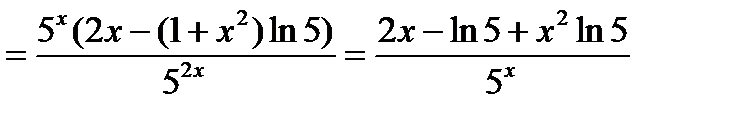
Дифференциал функции
Определение: Дифференциалом функции y=y(x) называется произведение ее производной на дифференциал независимой переменной:
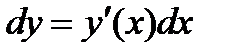 .
.
Для большей наглядности рассмотрим пример.
Пример 1: Найти дифференциал функции 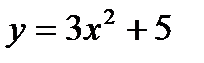
Решение: 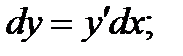
Так как  , то
, то 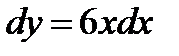 .
.
Дифференцирование сложной функции
Пусть y= y(u), где u= u(x) – дифференцируемые функции. Тогда сложная функция y=y[u(x)] есть также дифференцируемая функция, причем
 , или
, или 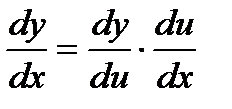
Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.
Производные сложных функций находятся при помощи таблицы:
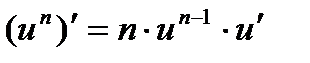

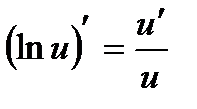

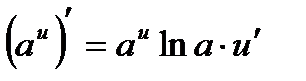
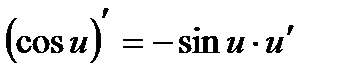
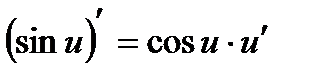

| 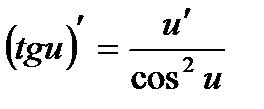
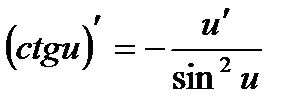

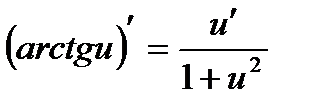
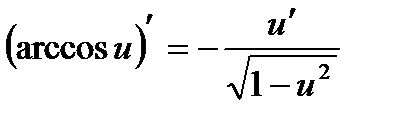

|
Рассмотрим примеры.
Пример 1: Найти производную функции 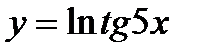
Решение: 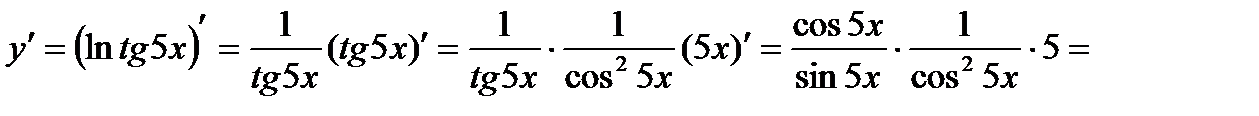 =
= 
Пример 2: Найти производную функции 
Решение: 
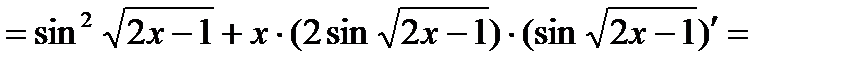
= 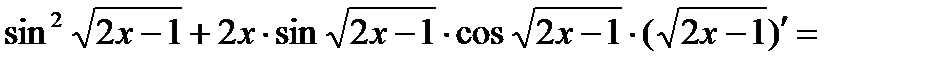
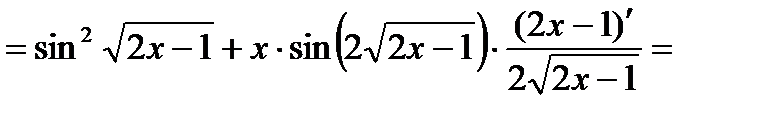
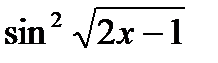 +
+

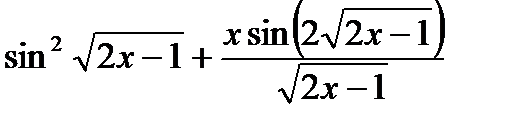
|
|
|



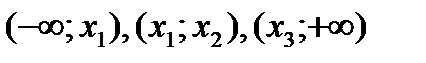
 точки локального экстремума.
точки локального экстремума.