Свойства определенного интеграла

Правило вычисления определённого интеграла от данной функции

1. Найти соответствующий неопределённый интеграл;
2. В полученное его выражение подставить вместо х сначала верхний предел интегрирования, а затем нижний.
3. Из первого результата вычесть второй.

При вычислении определённого интеграла от функции 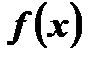пользуются записью: 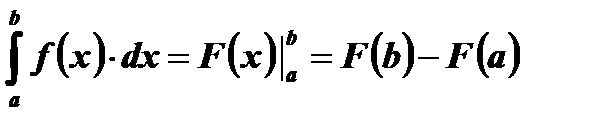(формула Ньютона-Лейбница).

 

1. Вычисление определенного интеграла способом подстановки

При вычислении определённого интеграла так же приходится применять различные приёмы, в том числе и способ подстановки. Подстановка в определённом интеграле делается аналогично подстановке в неопределённом интеграле, но, кроме того, для получающегося интеграла нужно находить новые пределы интегрирования.

Правило:

9) Определить, к какому табличному интегралу приводится данный интеграл;

10) Определить, какую часть подынтегральной функции необходимо заменить новой переменной, записать эту замену;

11) Вычислить дифференциал новой переменной и выразить через него оставшуюся без замены часть подынтегрального выражения;

12) Найти пределы интегрирования для новой переменной;

13) Выполнить замены под знаком интеграла;

14) Вынести за знак интеграла постоянный множитель;

15) Вычислить полученный табличный интеграл;

16) В полученное его выражение подставить вместо новой переменной сначала верхний предел интегрирования, а затем нижний, из первого результата вычесть второй.

 

Свойства определенного интеграла

1. Определенный интеграл не зависит от обозначения переменной интегрирования:

Это следует из того, что интегральная сумма, а, следовательно, и ее предел не зависят от того, какой буквой обозначается аргумент данной функции.

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: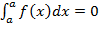

3. Для любого действительного числа с:

4. Для интегрируемой на отрезке 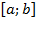функции справедливо

5. для функций, интегрируемых на отрезке и

6. Константу можно выносить за знак определенного интеграла, для функций, интегрируемых на отрезке , и константы k справедливо равенство

7. Если функция интегрируема на интервале X, причем , , , то выполняется . Это свойство выполняется для

8. Если функция интегрируема на интервале , то она интегрируема на любом внутреннем интервале .

 

Практическая часть:

Примеры задач:

1. Скорость движения тела в момент времени t задается формулой , где v- скорость, м/с; t-время, с. Какой путь пройдет тело от начала отсчета времени до остановки?

Решение. Так как в момент остановки тела скорость его равна 0, то нам нужно определить путь, пройденный телом от момента времени =0 до =5 с. Согласно формуле, получим

2. Материальная точка M движется по координатной прямой под действием силы, величина которой меняется прямо пропорционально расстоянию точки до начала координат О. Известно, что направление силы совпадает с направлением оси и что она равнялась 1 Н, когда расстояние МО было 3 м. Вычислить работу этой силы по переносу точки на расстояние 15 м от начала координат.

Решение. Из условия задачи следует что сила F(x), действующая на точку, меняется по закону F(x)=kx, где коэффициент пропорциональности k находится из уравнения 1=k*3, k=1/3. Таким образом, F(x)=x/3 и работа силы на пройденном пути равна

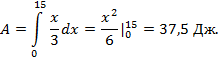
3. Вычислить силу давления воды на треугольную пластину АВС с основанием АС=9 м и высотой ВD=2 м, вертикально погруженную, если вершина В лежит на свободной поверхности жидкости, а АС- параллельно ей.

Решение. Пусть МN- поперечное сечение пластины на уровне ВЕ=x. Найдем зависимость длины MN от x. Из подобия треугольников MBN и АВС имеем МN/AC=BE/BD или MN/9=x/2. Отсюда MN=f(x)=4,5x. На основании формулы получим

 

 

Задача:

Два электрических заряда e₁ и e₂ по 10 Кл каждый закреплены неподвижно на расстоянии 5 см друг от друга. Разделяющей их средой служит воздух. Затем заряд e₂ освобождается и удаляется от заряда e₁ под действием силы отталкивания, которая меняется по закону Кулона

Где F-сила, H; е₁, е₂-заряды, Кл; r- расстояние между ними, см; - относительная диэлектрическая проницаемость среды, k=9*10⁹ H*м²/Кл² коэффициент пропорциональности. Какую работу совершит сила отталкивания, если заряд е₂ удалится от е₁ на расстояние 10 см?

Решение. воздуха=1; e₁,e₂,ε,k- константы, по отношению к r, r-изменяемая величина.

 

Список литературы:

Поделиться:

Воспользуйтесь поиском по сайту: