 |
II. Лабораторная установка и метод измерения
|
|
|
|
I. Теоретическое введение
В результате многочисленных экспериментов установлено, что свойства большинства веществ, находящихся в газообразном состоянии при не очень большом давлении, могут быть описаны уравнением Менделеева — Клапейрона:
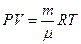 . (1)
. (1)
Здесь  - масса газа заключенного в объем
- масса газа заключенного в объем  при давлении
при давлении  и температуре
и температуре  ,
,  — число молей газа, величина
— число молей газа, величина 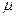 — масса одного моля,
— масса одного моля,  - универсальная газовая постоянная. Молем (моль) называется количество вещества, масса которого, выраженная в граммах, численно равна его весу в атомных единицах массы (см. периодическую таблицу Менделеева). Например, для азота
- универсальная газовая постоянная. Молем (моль) называется количество вещества, масса которого, выраженная в граммах, численно равна его весу в атомных единицах массы (см. периодическую таблицу Менделеева). Например, для азота 
 , кислорода
, кислорода 
 , паров воды
, паров воды 
 . Воздух является смесью газов - он состоит из азота (78% по объему), кислорода (21%) и остальная доля (порядка 1%) образована аргоном, гелием, неоном, углекислым газом, парами воды, поэтому для воздуха
. Воздух является смесью газов - он состоит из азота (78% по объему), кислорода (21%) и остальная доля (порядка 1%) образована аргоном, гелием, неоном, углекислым газом, парами воды, поэтому для воздуха  .
.
В одном моле вещества содержится одинаковое число молекул, это число называется числом Авогадро  . Согласно закону Авогадро, 1 моль идеального газа при нормальных условиях: температуре
. Согласно закону Авогадро, 1 моль идеального газа при нормальных условиях: температуре 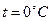 , т.е.
, т.е. 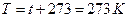 , давлении
, давлении 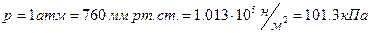 , занимает объем
, занимает объем  . Подставляя эти данные в формулу (1) закона Менделеева-Клайперона при
. Подставляя эти данные в формулу (1) закона Менделеева-Клайперона при 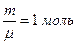 , получим значение универсальной газовой постоянной
, получим значение универсальной газовой постоянной 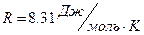 .
.
Уравнение Менделеева—Клапейрона хорошо описывает свойства разреженных газов, плотность которых  примерно в
примерно в  раз меньше плотности жидкости
раз меньше плотности жидкости  . В жидкости молекулы расположены очень близко друг к другу. Отсюда следует, что в разреженных газах среднее расстояние
. В жидкости молекулы расположены очень близко друг к другу. Отсюда следует, что в разреженных газах среднее расстояние  между молекулами в десятки раз больше их собственных размеров
между молекулами в десятки раз больше их собственных размеров  , т.е.
, т.е.  . Молекулы разреженного газа, находящегося при температуре
. Молекулы разреженного газа, находящегося при температуре  , совершают хаотическое тепловое движение, свободно пробегая путь между двумя последовательными столкновениями друг с другом или со стенками сосуда. Соударения молекул друг с другом или со стенками сосуда происходят без потери энергии, по законам соударения упругих тел. Это основное представление для молекулярно-кинетической теории идеальных газов. Оно позволяет объяснить их свойства. Согласно этой теории, молекулы-«шарики» (аргона, гелия, неона) движутся между упругими столкновениями поступательно. Такому движению соответствует число степеней свободы, равное
, совершают хаотическое тепловое движение, свободно пробегая путь между двумя последовательными столкновениями друг с другом или со стенками сосуда. Соударения молекул друг с другом или со стенками сосуда происходят без потери энергии, по законам соударения упругих тел. Это основное представление для молекулярно-кинетической теории идеальных газов. Оно позволяет объяснить их свойства. Согласно этой теории, молекулы-«шарики» (аргона, гелия, неона) движутся между упругими столкновениями поступательно. Такому движению соответствует число степеней свободы, равное
|
|
|
 (2)
(2)
Напомним, что числом степеней свободы называется число независимых координат, которое надо задать для определения положения тела в пространстве. Для поступательного движения тела в пространстве это координаты  . Следовательно,
. Следовательно,  . Молекулы-«гантельки» двухатомных газов (водорода, азота, кислорода) могут двигаться как поступательно (поступательное движение центра массы молекулы,
. Молекулы-«гантельки» двухатомных газов (водорода, азота, кислорода) могут двигаться как поступательно (поступательное движение центра массы молекулы,  ), так и вращаться вокруг осей, проходящих через центр массы молекулы:
), так и вращаться вокруг осей, проходящих через центр массы молекулы:  . Вращением молекулы вокруг продольной оси пренебрегаем, так как такому движению соответствует малое значение момента инерции по сравнению с другими осями.
. Вращением молекулы вокруг продольной оси пренебрегаем, так как такому движению соответствует малое значение момента инерции по сравнению с другими осями.
В результате для молекул-«гантелек» получим:
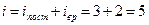 (3)
(3)
Тогда упрощенная механическая модель молекул позволяет объяснить основные свойства идеальных газов.
Согласно молекулярно-кинетической теории идеального газа средняя кинетическая энергия одной молекулы пропорциональна абсолютной температуре Т газа:
 ,
, 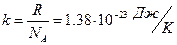 , (4)
, (4)
где 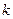 — постоянная Больцмана,
— постоянная Больцмана,  — число степеней свободы молекул газа (см. (2) и (3)).
— число степеней свободы молекул газа (см. (2) и (3)).
Полный запас внутренней энергии газа, заключенного в сосуд объемом  при температуре
при температуре  , получим умножением
, получим умножением  на число молекул
на число молекул  газа:
газа:
 . (5)
. (5)
Значение внутренней энергии газа  , заключенного в закрытый сосуд объемом
, заключенного в закрытый сосуд объемом  при давлении
при давлении  и температуре
и температуре  (см. рис. 1), можно изменить в результате внешних воздействий — передавая газу тепло
(см. рис. 1), можно изменить в результате внешних воздействий — передавая газу тепло  (нагрев
(нагрев  , охлаждение
, охлаждение  ) и совершая над газом работу
) и совершая над газом работу  под действием внешней силы
под действием внешней силы  ;
; 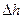 — смещение поршня сечения
— смещение поршня сечения  . Очевидно, что
. Очевидно, что  .
.
|
|
|


Переданное тепло  и работа внешних сил
и работа внешних сил  изменяют внутреннюю энергию на некоторое значение
изменяют внутреннюю энергию на некоторое значение  . Эти величины связаны между собой законом сохранения энергии, который для систем многих частиц называется первым законом термодинамики:
. Эти величины связаны между собой законом сохранения энергии, который для систем многих частиц называется первым законом термодинамики:
 ,
,
или
 , (6)
, (6)
где 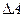 — работа газа против внешних сил, поскольку
— работа газа против внешних сил, поскольку  .
.
.
Количество теплоты, переданное системе, расходуется на изменение внутренней энергии системы и на совершение системой работы против внешних сил.
Согласно (6), энергия хаотического теплового движения молекул  может быть преобразована в механическую работу
может быть преобразована в механическую работу  .
.
Рассмотрим вопрос о молярных теплоемкостях газов. Молярная теплоемкость  численно равна количеству тепла
численно равна количеству тепла  , которое надо сообщить одному молю этого вещества (масса
, которое надо сообщить одному молю этого вещества (масса  ), чтобы нагреть его на
), чтобы нагреть его на 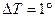 . Тогда можно записать
. Тогда можно записать  .
.
Для газов надо различать, при каких условиях происходит нагрев — например, при постоянном объеме  , или при постоянном давлении
, или при постоянном давлении  . Для процесса
. Для процесса  имеем
имеем 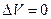 и
и  . Поэтому, согласно первому закону термодинамики (6), все сообщенное газу тепло
. Поэтому, согласно первому закону термодинамики (6), все сообщенное газу тепло  идет на увеличение внутренней энергии
идет на увеличение внутренней энергии  газа.
газа.
 (7)
(7)
Для процесса  газ расширяется, и сообщаемое тепло
газ расширяется, и сообщаемое тепло  идет на увеличение внутренней энергии
идет на увеличение внутренней энергии  и на работу
и на работу  против внешних сил:
против внешних сил:  (см. (6)). Увеличение объема
(см. (6)). Увеличение объема  можно найти из уравнения состояния идеального газа (1). При
можно найти из уравнения состояния идеального газа (1). При  имеем
имеем  . Подставляя это
. Подставляя это  в выражение для работы, получим
в выражение для работы, получим 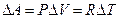 . Отсюда, используя (6), (7), получим выражение для теплоемкости одного моля идеального газа при постоянном давлении
. Отсюда, используя (6), (7), получим выражение для теплоемкости одного моля идеального газа при постоянном давлении  :
:
 . (8)
. (8)
Согласно (7), (8), теплоемкости 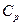 и
и  зависят от R и числа степеней свободы i молекул идеального газа. Для одноатомного газа (молекулы-«шарики»)
зависят от R и числа степеней свободы i молекул идеального газа. Для одноатомного газа (молекулы-«шарики»)  , для двухатомного газа (молекулы-«гантельки») i=5 (см. формулу (3)). Отношение теплоемкостей
, для двухатомного газа (молекулы-«гантельки») i=5 (см. формулу (3)). Отношение теплоемкостей  равно:
равно:
 (9)
(9)
Согласно (2), для одноатомных газов, когда i=3, отношение  ; для двухатомных газов, когда i=5, имеем
; для двухатомных газов, когда i=5, имеем  . Напомним, что воздух образован смесью двухатомных газов — азота
. Напомним, что воздух образован смесью двухатомных газов — азота  и кислорода
и кислорода  (99% состава воздуха).
(99% состава воздуха).
В заключение рассмотрим основные газовые процессы при  и их графики (см. рис. 2).
и их графики (см. рис. 2).
Изохорический процесс:  ,
, 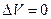 .
.
Согласно (1), (5), (7)
 ,
,  ,
,  . (10.1)
. (10.1)
Изобарический процесс:
 ,
,  ,
,  ,
,  ,
,  . (10.2)
. (10.2)
Изотермический процесс:
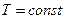 ,
,  ,
,  ,
,  . (10.3)
. (10.3)
Адиабатный процесс:  — имеет место при идеальной теплоизоляции или в случае очень быстрого процесса, при котором теплообмен между термодинамической системой и окружающей средой просто не успевает произойти. В этом случае
— имеет место при идеальной теплоизоляции или в случае очень быстрого процесса, при котором теплообмен между термодинамической системой и окружающей средой просто не успевает произойти. В этом случае  , т.е. расширение газа
, т.е. расширение газа  возможно только за счет внутренней энергии. При таком расширении газ охлаждается:
возможно только за счет внутренней энергии. При таком расширении газ охлаждается:  .
.
|
|
|
В данном приближении получим уравнение адиабатного процесса при  :
:  . Согласно (1), (8)
. Согласно (1), (8)  . Поделим уравнение
. Поделим уравнение  на
на  и
и  . В итоге:
. В итоге: 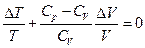 , или, переходя к бесконечно малым величинам, получаем уравнение
, или, переходя к бесконечно малым величинам, получаем уравнение  , где
, где  (см. (9)). Интегрируя это уравнение которое, получаем
(см. (9)). Интегрируя это уравнение которое, получаем  - уравнение адиабаты на плоскости переменных (T,V). Используя (1), на плоскости (P,V) запишем уравнение адиабаты в форме
- уравнение адиабаты на плоскости переменных (T,V). Используя (1), на плоскости (P,V) запишем уравнение адиабаты в форме
 (10.4)
(10.4)
Основные газовые процессы на плоскости  представлены на рис. 2. Рисунок выполнен для случая
представлены на рис. 2. Рисунок выполнен для случая  и так, что все процессы проходят через одну точку
и так, что все процессы проходят через одну точку 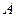 , в которой они пересекаются.
, в которой они пересекаются.

Рис. 2. Основные газовые процессы в идеальных газах
Из графиков на рис. 2 видно, что адиабата спадает круче изотермы, поскольку для нее значение  . Например, для двухатомных газов i=5 и значение
. Например, для двухатомных газов i=5 и значение 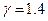 (см. (3), (9)).
(см. (3), (9)).
Условия, при которых протекают изотермический и адиабатический процессы. Процессы с 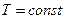 , т.е. с нулевым изменением температуры газа, возможны только при беспрепятственном теплообмене с окружающей средой. Адиабатический процесс с
, т.е. с нулевым изменением температуры газа, возможны только при беспрепятственном теплообмене с окружающей средой. Адиабатический процесс с  возможен только при полной теплоизоляции от окружающей среды. Полная теплоизоляция на практике не реализуется. Это условие приближенно выполнимо только для очень быстрых процессов.
возможен только при полной теплоизоляции от окружающей среды. Полная теплоизоляция на практике не реализуется. Это условие приближенно выполнимо только для очень быстрых процессов.
Процессы, занимающие промежуточное положение между двумя этими крайними случаями, осуществимыми на практике, называются политропными. Это процессы, при которых происходит частичный теплообмен со средой.
Политропные процессы. На плоскости  эти процессы представляются кривой политропы. Она занимает промежуточное положение между изотермой и адиабатой.
эти процессы представляются кривой политропы. Она занимает промежуточное положение между изотермой и адиабатой.
 ,
, 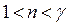 . (11)
. (11)
Изотермический и адиабатный процессы можно рассматривать как частные случаи политропного процесса (для которых  и
и  ). Численные значения n определяются экспериментально. На рис. 2 политропный процесс вида (11) качественно представлен пунктирной линией.
). Численные значения n определяются экспериментально. На рис. 2 политропный процесс вида (11) качественно представлен пунктирной линией.
|
|
|
Представления об основных газовых процессах (см. рис. 2) используются в различных областях науки и техники. Например, процесс сжатия газов в звуковой волне акустических частот  диапазона
диапазона  Гц в атмосфере Земли является адиабатическим процессом, так как рассматриваемый процесс достаточно быстрый. Максимальный период
Гц в атмосфере Земли является адиабатическим процессом, так как рассматриваемый процесс достаточно быстрый. Максимальный период  соответствует частоте
соответствует частоте  Гц и составляет
Гц и составляет  секунд. При распространении волны образуются области повышенного и пониженного давления относительно давления атмосферного. Однако чередование процессов сжатия и разряжения в этих областях происходит настолько быстро, что теплообмен между такими областями не успевает произойти. Соответственно, различие между экспериментальными скоростями распространения звука и теоретическими значениями не превосходит 1%.
секунд. При распространении волны образуются области повышенного и пониженного давления относительно давления атмосферного. Однако чередование процессов сжатия и разряжения в этих областях происходит настолько быстро, что теплообмен между такими областями не успевает произойти. Соответственно, различие между экспериментальными скоростями распространения звука и теоретическими значениями не превосходит 1%.
Процесс сжатия горючей смеси в двигателях внутреннего сгорания происходит достаточно быстро, но, как известно, в этих двигателях используется система охлаждения. Следовательно, эти процессы не являются адиабатными. В различных автомобильных фирмах разработаны установки для экспериментального измерения показателя политропы n (11). Знание значения n позволяет конструкторам согласовывать движение поршня с упругими свойствами рабочей смеси. В результате удается повысить экономические показатели работы двигателя и снизить расход бензина.
II. Лабораторная установка и метод измерения
Для измерения соотношения  (10.4) изготовлена лабораторная установка (рис. 3), в которой в качестве рабочего тела используется воздух.
(10.4) изготовлена лабораторная установка (рис. 3), в которой в качестве рабочего тела используется воздух.

На рис. 3 показаны: 1 — сосуд с воздухом, 2 — водяной манометр U-образной формы (для удобства измерений вода подкрашена), 3 — кран, соединяющий сосуд с атмосферой или с насосом, h — разности уровней водяного столба в манометре, 4 — насос. На этом рисунке показания манометра соответствуют давлению в сосуде  ,
,  — плотность воды,
— плотность воды,  .
.
В этой установке можно выполнить два процесса: адиабатическое расширение, при котором воздух в установке охлаждается до  ; изохорический процесс нагревания воздуха от
; изохорический процесс нагревания воздуха от  до
до  . Графики этих процессов на плоскости
. Графики этих процессов на плоскости  , реализуемых в лабораторной установке, проведены на рис. 4.
, реализуемых в лабораторной установке, проведены на рис. 4.
1. Исходное состояние (точка (1) на рис. 4) с  и
и  получают, предварительно накачав насосом воздух в сосуд до давления
получают, предварительно накачав насосом воздух в сосуд до давления  . Для этого предварительно соединяют краном 3 сосуд 1 с насосом 4. Затем, после накачивания, кран закрывают. Когда показания манометра станут стабильными (газ остынет после накачивания и температура станет равной температуре среды (комнатной температуре:
. Для этого предварительно соединяют краном 3 сосуд 1 с насосом 4. Затем, после накачивания, кран закрывают. Когда показания манометра станут стабильными (газ остынет после накачивания и температура станет равной температуре среды (комнатной температуре:  )), измеряют давление
)), измеряют давление  :
:
|
|
|
 (12)
(12)
и записывают значение  разности высот в коленах манометра в таблицу. Рекомендованные значения
разности высот в коленах манометра в таблицу. Рекомендованные значения  составляют
составляют  сантиметров.
сантиметров.
2. Открывают кран (3), сообщая сосуд с атмосферой. При этом часть воздуха выходит в атмосферу, и давление газа быстро выравнивается с атмосферным давлением  (точка (а) на рис. 4).
(точка (а) на рис. 4).

Рис. 4. Графики процессов, реализуемых в лабораторной установке
После этого кран быстро закрывают (при показаниях манометра  ). Таким образом, оставшаяся часть воздуха массой
). Таким образом, оставшаяся часть воздуха массой  расширилась и заняла весь объем сосуда
расширилась и заняла весь объем сосуда 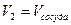 . Заметим, в первом состоянии
. Заметим, в первом состоянии  эта масса воздуха
эта масса воздуха  занимала только часть объема
занимала только часть объема  . Если выполненный процесс расширения происходит достаточно быстро, без теплообмена с атмосферой, то для такой массы газа
. Если выполненный процесс расширения происходит достаточно быстро, без теплообмена с атмосферой, то для такой массы газа  применим закон адиабатического расширения
применим закон адиабатического расширения
 , или
, или 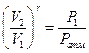 (13)
(13)
Здесь необходимо учитывать, что в точке (а) объем 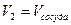 , а давление равно
, а давление равно  . В результате этого расширения воздух в сосуде охладился до температуры
. В результате этого расширения воздух в сосуде охладился до температуры  , а его давление уменьшилось до
, а его давление уменьшилось до  .
.
3. Последний переход. Газ в сосуде в результате контакта с окружающей средой нагревается при постоянном объеме до комнатной температуры  (точка (2) на рис. 4). Здесь давление
(точка (2) на рис. 4). Здесь давление  можно определить по показаниям манометра
можно определить по показаниям манометра 
 . (14)
. (14)
Показания манометра  необходимо занести в таблицу.
необходимо занести в таблицу.
Таким образом: состояния «1» и «2» имеют одинаковые температуры  и, следовательно, из уравнения Менделеева-Клапейрона имеем
и, следовательно, из уравнения Менделеева-Клапейрона имеем
 ; (15)
; (15)
состояния «1» и «а» связаны адиабатическим процессом, для которого выполняется формула (13).
Выполним теперь необходимые расчеты для получения значения показателя политропы. Введем для удобства записи обозначения  . При этом
. При этом  ,
,  . Подставляя (15) в (13) и логарифмируя, находим:
. Подставляя (15) в (13) и логарифмируя, находим:
 (16)
(16)
Здесь введены обозначения  . В последнем приближенном равенстве в (16) учтено известное в математике представление
. В последнем приближенном равенстве в (16) учтено известное в математике представление 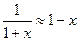 , справедливое при
, справедливое при  , где
, где  , а также пренебрегается малым (по сравнению с остальными) слагаемым
, а также пренебрегается малым (по сравнению с остальными) слагаемым  . Далее учитываем применительно к числителю и знаменателю последнего выражения в формуле (16) известное соотношение
. Далее учитываем применительно к числителю и знаменателю последнего выражения в формуле (16) известное соотношение  , справедливое при условии
, справедливое при условии  (действительно, в условиях эксперимента не только
(действительно, в условиях эксперимента не только  , но и
, но и  ). В результате получим окончательное расчетное выражение для определения искомого значения
). В результате получим окончательное расчетное выражение для определения искомого значения  :
:
 . (17)
. (17)
III. Расчет погрешности найденного значения 
Расчет абсолютной погрешности найденного значения  можем провести по формуле, совпадающей с формулой расчета погрешности в случае прямых измерений. Это связано с тем, что число проведенных экспериментов (а именно 10) много больше единицы. В этом случае абсолютная погрешность
можем провести по формуле, совпадающей с формулой расчета погрешности в случае прямых измерений. Это связано с тем, что число проведенных экспериментов (а именно 10) много больше единицы. В этом случае абсолютная погрешность  вычисляется по формуле
вычисляется по формуле
 .
.
Здесь  , среднее значение
, среднее значение  ,
, 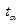 - коэффициент Стьюдента, соответствующий числу опытов
- коэффициент Стьюдента, соответствующий числу опытов  и выбранному значению доверительной вероятности, которое принимаем равным
и выбранному значению доверительной вероятности, которое принимаем равным  или
или  (см. методическое пособие «Обработка результатов физического эксперимента»). Относительная погрешность равна
(см. методическое пособие «Обработка результатов физического эксперимента»). Относительная погрешность равна 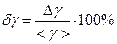 .
.
Расчет абсолютной погрешности значения  можно провести и по методу, отвечающему косвенным измерениям (см. методическое пособие «Обработка результатов физического эксперимента»):
можно провести и по методу, отвечающему косвенным измерениям (см. методическое пособие «Обработка результатов физического эксперимента»):
 (18)
(18)
и далее сравнить полученные результаты.
На основе изложенных рассуждений в работе определяется коэффициент адиабаты  (см. Первый способ измерения). Однако трудность состоит в том, что адиабатный процесс занимает малые доли секунды, а момент его завершения, когда требуется закрыть клапан, неизвестен.
(см. Первый способ измерения). Однако трудность состоит в том, что адиабатный процесс занимает малые доли секунды, а момент его завершения, когда требуется закрыть клапан, неизвестен.
Поэтому P" определяется следующим косвенным методом. При одинаковом начальном давлении P', но разной длительности t открытия крана (3), соединяющего сосуд с атмосферой,измеряют конечное давление  . Закономерности теплообмена между газом и окружающей средой таковы, что зависимость
. Закономерности теплообмена между газом и окружающей средой таковы, что зависимость  можно приближенно описать экспоненциальной функцией вида
можно приближенно описать экспоненциальной функцией вида
 ,
,
где  — длительность адиабатного процесса,
— длительность адиабатного процесса,  — постоянный коэффициент, характеризующий скорость теплообмена. Пренебрегая
— постоянный коэффициент, характеризующий скорость теплообмена. Пренебрегая  по сравнению с t и логарифмируя обе части последнего равенства, приходим к выражению:
по сравнению с t и логарифмируя обе части последнего равенства, приходим к выражению:
 (19)
(19)
Поскольку  ,
, 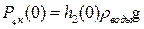 , то с учетом свойств логарифма получаем:
, то с учетом свойств логарифма получаем:

Так как  линейно зависит от времени, и при t→ 0 стремится к
линейно зависит от времени, и при t→ 0 стремится к  , то точка пересечения экспериментально найденного линейного графика с вертикальной линией при t=0 позволяет найти
, то точка пересечения экспериментально найденного линейного графика с вертикальной линией при t=0 позволяет найти  и определить
и определить 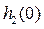

IV. Выполнение работы
I. Первый способ измерения
1. Открыть кран и накачать воздух в сосуд так, чтобы разность уровней в коленах манометра достигла  см.
см.
2. Закрыть кран и после того, как давление в сосуде установится, произвести отсчет разности уровней высот  уровней жидкости в коленах манометра.
уровней жидкости в коленах манометра.
3. Открыть кран, на короткое время соединяя сосуд с атмосферой. Как только уровни в коленах манометра сравняются, кран быстро закрыть.
4. Когда произойдет теплообмен с окружающей средой и давление установится, измерить разность значений  и
и  в коленах манометра.
в коленах манометра.
5. Измерения по пп. 1 повторить 10 раз, беря разные значения  . Результаты измерений значений
. Результаты измерений значений  и
и  занести в таблицу.
занести в таблицу.
| № опыта | 
| 
| 
| <  > >
|
6. Вычислить по формуле (17) значения  для каждого измерения, найти среднее арифметическое значение
для каждого измерения, найти среднее арифметическое значение  .
.
7. Определить абсолютную  и относительную
и относительную  ошибку значений
ошибку значений  (см. методическое пособие «Обработка результатов измерений»).
(см. методическое пособие «Обработка результатов измерений»).
8. По формуле (9) подсчитать значения  для основных газов, из которых состоит воздух (азот, кислород, аргон, углекислый газ, пары воды).
для основных газов, из которых состоит воздух (азот, кислород, аргон, углекислый газ, пары воды).
9. Сравнить <  > со значением n для политропного процесса (11).
> со значением n для политропного процесса (11).
II. Второй способ измерения.
1. Открыть кран и накачать воздух в сосуд так, чтобы разность уровней  в коленах манометра достигла уровня 21 см. Затем кран закрыть.
в коленах манометра достигла уровня 21 см. Затем кран закрыть.
2. Дождаться, когда температура в сосуде станет равна комнатной, признаком чего станет прекращение изменения положения уровней жидкости в коленах манометра. При всех опытах стремиться к тому, чтобы соответствующая разность уровней в коленах манометра была бы одинаковой. Если это не выполняется, необходимо немного подкачать воздух или, напротив, слегка его выпустить с тем, чтобы величина  во всех опытах была бы одинаковой.
во всех опытах была бы одинаковой.
3. Открыть кран соединения с атмосферой и закрыть его через требуемое время. Рекомендуемые значения t: 6 сек; 8 сек; 10 сек. Прошедшее время измеряется секундомером. Занести реальное время t, в течение которого был открыт клапан, в таблицу.
| № опыта | 
| t | 
|
4. Дождаться, когда температура в баллоне сравняется с температурой в лаборатории. Занести в таблицу значение  .
.
5. По полученным данным построить график зависимости  и графически вычислить значение
и графически вычислить значение  (см. рис. 5). После чего, полагая в формуле (17)
(см. рис. 5). После чего, полагая в формуле (17)  , найти искомое значение
, найти искомое значение  .
.
6. Сравните найденные способами (I) и (II) значения  . Сделайте вывод.
. Сделайте вывод.
Контрольные вопросы
1. Физическая модель идеального газа. Уравнение состояния идеального газа.
2. Молярная, удельная и полная теплоемкости.
3. В каких единицах измеряются в системе СИ давление, объем, температура, молярные теплоемкости?
4. Что такое молярные теплоемкости Ср и Сv?
5. Что такое адиабатный процесс?
6. Что такое изотермический процесс?
7. Что такое изобарный процесс?
8. Что такое изохорный процесс?
9. Понятие политропного процесса.
10. Вывод расчетной формулы для определения  .
.
11. Изобразите в координатах P–V изохорное охлаждение, изобарное нагревание, изотермическое и адиабатическое расширение, начинающиеся из одного начального состояния.
12. Как найти бесконечно малое изменение внутренней энергии и бесконечно малую работу, совершаемую идеальным газом в некотором термодинамическом процессе?
13. Как связаны молярные теплоемкости Ср и С v с числом степеней свободы молекулы i? Каково теоретическое значение  ?
?
14. Что такое уравнение Пуассона?
15. Как изменяется давление некоторого количества воздуха при адиабатном увеличении его объема в два раза?
16. Выведите формулу (18) для расчета 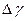 .
.
17. Решите задачи № 5. 187, 5.158, 5.160. из «Сборника задач по общему курсу физики» (Волькенштейн В.С. Изд. «Книжный мир». СПБ. 2003.)
ЛИТЕРАТУРА
1. Савельев И.В. Курс общей физики. Т.1. § 15. Изд. «Лань». СПБ. 2005
2. Яворский Б. М., Пинский А. А. Основы физики, т. I. М.: Наука, 1974. 496 с.
3. Волькенштейн В.С. Сборник задач по общему курсу физики. М.: Наука, 2003. 220 с.
4. Яворский Б. М., Детлаф А. А. Справочник по физике, М.: Наука, 1964. 847 с.
Лев Петрович Коган
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА
Методические указания к выполнению лабораторной работы № 4
для студентов специальностей 140100, 230400.62, 120700.62, 270800.62, 221700.62, 022000.62, 271101, 271101.
_________________________________________________
Подписано в печать ______. Формат 60 x 90. 1/16. Бумага газетная. Печать трафаретная. Уч. изд. л. ____. Усл. печ. л. ____. Тираж 150 экз. Заказ № ____
________________________________________________________________________
Федеральное агентство по образованию.
Государственное образовательное учреждение высшего профессионального образования «Нижегородский государственный строительный университет»
603950, Н. Новгород, Ильинская, 65.
Полиграфцентр ННГАСУ, 603950 Н.Новгород, Ильинская, 65.
|
|
|


