Выдвижение гипотез о механизмах реакций

 

Выдвижение гипотез о механизмах исследуемых реакций является одним из этапов рациональной стратегии построения кинетических моделей. В случае каталитических реакций можно выделить следующие уровни гипотез:

§ гипотезы о состоянии катализатора, о природе активных центров;

§ гипотезы о возможных элементарных стадиях, которые могли бы реализоваться на данном катализаторе с выбранным набором реагентов;

§ гипотезы об отдельном механизме (схема механизма) образования заданных продуктов с минимальным набором маршрутов;

§ анализ узлов сопряжения маршрутов образования различных пар продуктов;

§ гипотеза о максимальном механизме (реакционная сеть, chemical reaction network) с анализом всех узлов сопряжения между интермедиатами.

Гипотезы о состоянии катализатора, о механизмах формирования активных центров из предшественников и о природе активного центра чрезвычайно важны для перехода к гипотезам следующего уровня – к элементарным стадиям (ЭС) и реакционным сетям (РС). Рассмотрим два характерных примера из области металлокомплексного катализа. В реакциях, катализируемых комплексами Pd из предшественников PdX₂ и PR₃ могут сформироваться в зависимости от реагентов и среды комплексы Pd(II) – PdX₂(PR₃)₂, Pd(0) – Pd(PR₃)n и Pd(I) – Pd₂X₂(PR₃)₂. Очевидно, что палладий в разных степенях окисления будет способен участвовать в разных по природе стадиях механизма. Например, Pd(II) – окислитель, акцептор пар электронов, мягкая апротонная кислота, а Pd(0) – восстановитель, донор пар электронов, мягкое основание. Так, механизмы одной и той же реакции алкоксикарбонилирования ацетилена с образованием акрилата (А) на этих двух частицах в спиртовых растворах принципиально различны:

 

В первом случае вначале активируется спирт (S_E), а затем СО и С₂Н₂, во втором – реакция начинается с окислительного присоединения HX, затем в реакцию вступают ацетилен, СО и ROH. Таким образом, выбор возможных стадий и схем механизма прежде всего определяется свойствами металлокомплекса в растворе или свойствами активного центра на поверхности.

Выдвижение гипотез – процедура творческая, основанная на знаниях и интуиции. Вместе с тем, существуют и частично или полностью формализованные методы, которые позволяют получить максимально полные наборы гипотез при заданных ограничениях. Рассмотрим некоторые из них.

 

Использование условий ортогональности .

 

Условие ортогональности стехиометрической матрицы механизма  и атомной матрицы  позволяет восстановить матрицу В, если заданы все участники реакции и возможные интермедиаты, т.е. найти все возможные элементарные стадии образования и превращения заданных интермедиатов при определенных ограничениях, например, на молекулярность ЭС. Этот путь, однако, не очень эффективен, поскольку придумать интермедиаты процесса не легче, чем весь механизм, и процедура формального поиска взаимосвязей между интермедиатами (ЭС) незначительно облегчает задачу.

Математическая модель структурной химии Дугунджи-Уги.

 

В рамках этой модели каждая химическая реакция рассматривается как изомеризация ансамблей атомов – ансамбля реагентов в ансамбль продуктов. Например, реакция (1)

                                                       (1)

катализируется катализатором М. Тогда исходный ансамбль (ЕМ_исх) есть {M, HCl, C₂H₂}, а конечный ансамбль (ЕМ_кон) – {M, CH2=CHCl}. Число атомов каждого сорта в процессе изомеризации ансамбля не меняется (SN = const). Атомы, входящие в ансамбль А = <M,H,Cl,C,C,H,H>. Отыскание механизма суть отыскание последовательности изомеризации ансамблей.

ЕМ_исх ® ЕМ₁ ® ЕМ₂ ® ЕМ_кон

Каждый ансамбль атомов представляется специальной be-матрицой (bond-electron), а переход исходного ансамбля В в конечный ансамбль Е в каждой реакции осуществляется с помощью реакционной R -матрицы

B + R = E                                                                                   (2)

Например, для реакции

                                              (3)

матрицы В, Е и R являются квадратными матрицами, недиагональные элементы которых b_ij равны числу связей атома i и атома j, а диагональные элементы b_ij (i = j) равны числу валентных электронов на атоме i в соответствующем соединении. R = E – B.

 

 

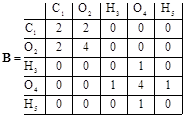
Для генерации гипотез этим методом используют набор стандартных R матриц, и каждую матрицу применяют к каждому последующему ансамблю или находят все возможные R -матрицы, удовлетворяющие заданным ограничениям и с ними генерируют все изомерные матрицы.

12	Поделиться:

Воспользуйтесь поиском по сайту: