 |
Материальные уравнения электромагнитного поля в среде с дисперсией.
|
|
|
|
Содержание.
Введение........................................................................................................................3
§ 1. Материальные уравнения электромагнитного поля в среде с дисперсией.....5
§ 2. Закон дисперсии. Вектор объемной плотности поляризации.........................10
§ 3. Зависимость показателя преломления и поглощения от частоты..................12
Заключение.................................................................................................................15
Литература..................................................................................................................16
Введение.
Важнейшей характеристикой линейной распределенной системы является закон дисперсии, который связывает волновое число и частоту монохроматической волны. Он может быть записан как 
, 
или в неявной форме 
.
Когда плоская волна описывается одним (вообще говоря, интегродифференциальным) уравнением, закон дисперсии получают, отыскивая его решение в виде 
. В простейшем случае процесс распространения волны описывается уравнением
.
При этом волновое число связано с частотой линейной зависимостью 
, или 
, где скорость распространения волны 
есть постоянная величина. Однако уже при учете диссипативных процессов поведение волны описывается более сложными уравнениями. Закон дисперсии 
также усложняется. Для звуковых волн в вязкой теплопроводящей среде и электромагнитных волн в среде с проводимостью справедливы следующие соотношения между волновым числом и частотой:
.
В более общих случаях от частоты могут сложным образом зависеть действительная и мнимая части волнового числа:
.
Действительная часть характеризует зависимость от частоты фазовой скорости распространения волны 
, а мнимая часть — зависимость коэффициента затухания волны от частоты.
|
|
|
Во многих случаях волновой процесс удобно описывать не одним уравнением типа волнового, а системой связанных интегродифференциальных уравнений 
. Здесь 
— матричный оператор, действующий на вектор-столбец 
.В качестве , например, для акустических волн может служить совокупность переменных 
(колебательная скорость, приращения плотности, давления, температуры), а для электромагнитных волн — компоненты векторов напряженностей электрического и магнитного полей, электрического смещения и магнитной индукции. В этом случае формальная схема отыскания закона дисперсии такова. Ищем решение системы в виде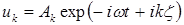 
:
,
Решение будет нетривиальным, только если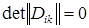 
. Отсюда получаются искомые зависимости 
. Наличие у дисперсионного уравнения нескольких корней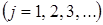 
означает, что система может описывать несколько типов собственных волн (мод) среды.
Частотная дисперсия приводит к изменению закономерностей распространения немонохроматических волн. Действительно, различные спектральные компоненты обладают в диспергирующей среде отличающимися скоростями и коэффициентами затухания:
.
В силу дисперсии фазовой скорости в процессе распространения изменяются фазовые соотношения между спектральными компонентами. Следовательно, изменяется результат их интерференции: форма немонохроматической волны искажается. Дисперсия коэффициента поглощения 
приводит к трансформации частотного спектра волны 
и дополнительному искажению формы импульса.
Материальные уравнения электромагнитного поля в среде с дисперсией.
Дисперсионные эффекты часто проявляются при распространении электромагнитных волн. Покажем, как видоизменяются исходные уравнения при учете этих свойств. Система уравнений Максвелла сохраняет свой вид. Свойства среды должны быть учтены в материальных уравнениях:
.
Для статических и медленно изменяющихся полей можно написать
|
|
|
,
где 
— константы, т. е. значения 
и 
в некоторой точке среды и в некоторый момент времени определяются значениями 
и 
в той же точке и в тот же момент времени.
При быстром изменении поля вследствие инерции внутренних движений и наличия пространственной микроструктуры среды наблюдается зависимость поляризации от поля, действующего в других точках и в другие моменты времени. При этом нужно иметь в виду, что в силу условия причинности поляризация и, следовательно, индукция зависят от полей, действовавших только в предыдущие моменты времени.
Сказанное можно записать математически, представляя материальные уравнения в общей интегральной форме:
, (1.1)
, (1.2)
. (1.3)
По дважды встречающимся индексам здесь и везде в дальнейшем предполагается суммирование.
Выражения (1.1) — (1.3) представляют собой наиболее общую функциональную форму записи материальных уравнений для линейной среды. В этой записи учтена возможность проявления нелокальности, запаздывания и анизотропных свойств среды.
В частном случае, если среда однородна в пространстве и не изменяет со временем своих свойств, материальные характеристики 
, 
, 
должны зависеть лишь от разностей координат 
и времени 
. Тогда
, (1.4)
, (1.5)
. (1.6)
Связь между электрическим смещением и магнитной индукцией, полями и поляризациями среды определяется соотношениями
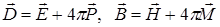. (1.7)
Поэтому материальные уравнения можно записать также в виде
, (1.8)
где 
— тензор восприимчивости среды. Аналогичное выражение можно записать для 
.
Для проведения дальнейшего анализа удобно разложить 
по плоским волнам:
.
После обычного перехода в фурье-представление в выражениях для 
и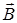 
получаем простую зависимость
, (1.9)
, (1.9)
|
|
|
где
. (1.10)
Видно, что компоненты тензора диэлектрической проницаемости зависят в общем случае от частоты и от волнового вектора волны.
Аналогичный вывод можно сделать для магнитной проницаемости 
и проводимости 
.
Таким образом, дисперсия при распространении электромагнитных волн может проявляться двояким образом — как частотная (за счет зависимости , 
, от частоты) и как пространственная (за счет зависимости этих же параметров от волнового вектора 
). Частотная дисперсия существенна, если частота электромагнитных волн близка к собственным частотам колебаний в среде. Пространственная же дисперсия становится заметной, когда длина волны сравнима с некоторыми характерными размерами.
Для электромагнитных волн в большинстве случаев, даже в оптическом диапазоне, характерный размер 
(где 
— длина волны в среде: 
) и пространственной дисперсией можно пренебречь. Однако в магнитоактивной плазме существуют области резонанса, в которых 
и параметр 
становится значительным уже в радиодиапазоне. Кроме того, при полном пренебрежении величинами, содержащими малое отношение 
, не учитываются некоторые явления, возникающие при распространении электромагнитных волн в различных средах. Так, учет пространственной дисперсии в плазме позволяет объяснить появление бегущих плазменных волн. Пространственная дисперсия является главной причиной (а не поправкой), вызывающей появление естественной оптической активности и оптической анизотропии кубических кристаллов. Если не интересоваться этими специальными случаями, то при рассмотрении частотной дисперсии пространственной дисперсией можно пренебречь.
При учете только частотной дисперсии материальное уравнение (1.9) имеет вид
. (1.11)
В отличие от (1.9) здесь взяты не компоненты плоских волн поля , а лишь временные гармоники. Диэлектрическая проницаемость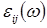 
для волны с частотой 
— это тензор, который в случае изотропной среды обращается в скаляр:
|
|
|
(1.12)
(напомним, что 
— действительная величина). Из (1.12) следует, что функция 
является комплексной:
, (1.13)
, (1.14)
т.е. 
является четной функцией, а 
— нечетной. Все сказанное справедливо также для 
:
. (1.15)
Если в недиспергирующей среде диэлектрическая проницаемость — чисто реактивный параметр, а проводимость — чисто активный, то в среде с дисперсией это различие утрачивается. С увеличением частоты до значений, близких к собственным частотам среды, различие в свойствах диэлектриков и проводников постепенно исчезает. Так, наличие у среды мнимой части диэлектрической проницаемости с макроскопической точки зрения неотличимо от существования проводимости — и то и другое приводит к выделению тепла. Поэтому электрические свойства вещества можно характеризовать одной величиной — комплексной диэлектрической проницаемостью
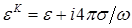, (1.16)
где 
.
Можно установить предельный вид диэлектрической проницаемости при больших частотах. В пределе при 
имеем
,
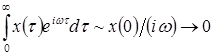и диэлектрическая проницаемость 
, определяемая выражениями (1.6), (1.12), стремится к единице при .
Это же свойство диэлектрической проницаемости следует и из простого физического рассмотрения. При , когда частота волны велика по сравнению с собственными частотами колебаний электронов в атомах вещества, электроны можно считать свободными. Уравнение движения свободного электрона под действием гармонического поля 
и решение этого Уравнения имеют вид
.
Здесь 
— масса и заряд электрона. Мы не учитываем силу, действующую на заряд со стороны магнитного поля, так как рассматривается нерелятивистский случай (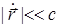
). Поляризация среды (дипольный момент единицы объема, содержащей 
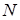электронов) равна
.
Отсюда 
и
. (1.17)
При 
мы получаем из (1.17) прежний результат: 
и 
. Область применимости формулы (1.17) для сред, в которых нет свободных электронов, лежит в диапазоне далекой ультрафиолетовой области для самых легких элементов.
С учетом (1.16) уравнения Максвелла для комплексных амплитуд примут вид
, (1.18)
. (1.18)
Поясним вывод уравнения 
. Из уравнения непрерывности при гармонической зависимости от времени следует, что
|
|
|
.
Подставляя это соотношение в уравнение Максвелла 
, запишем его в форме
.
Учитывая определение 
, получим уравнение .
Таким образом, для высокочастотных монохроматических полей вместо диэлектрической проницаемости и проводимости удобно ввести комплексную диэлектрическую проницаемость, объединяющую оба эти понятия. Физически это означает, что ток в среде для высокочастотных полей нецелесообразно рассматривать как сумму тока проводимости и тока смещения. Вместо этого вводится полный ток
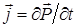, (1.19)
где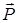 
— комплексный вектор поляризации среды.
|
|
|
