 |
Метод введения новой переменной.
|
|
|
|
Методы решения уравнений и неравенств повышенной сложности в математических олимпиадах
Яковлев Артем, 10 класс, Маряхичева О.А.., учитель математики
МБОУ «СОШ п.Опытный» Цивильского района ЧР
Краткая аннотация:
Ключевые слова: математика, уравнения, неравенства, нестандартные способы решения
Ежегодно я принимаю участие в олимпиадах по математике различного уровня, где встречаюсь с решением уравнений и неравенств. Я решил изучить нестандартные методы решения уравнений и неравенств, что бы применять их в следующем году. Поэтому
Цель моей работы: Изучить и научиться применять методы решения уравнений и неравенств, встречающихся в математических олимпиадах.
Задачи:
1) Изучить и разобрать различные методы решений уравнений и неравенств
2) Выбрать несколько наиболее простых и понятных способов решения
3) Попробовать применить эти способы решений в математических олимпиадах последних 3-ёх лет
4) Сделать вывод об актуальности этих методов в решении уравнений и неравенств в математических олимпиадах.
Исследуя литературу по данной теме, я выделил для себя 4 основных метода решения уравнений и неравенств:
1) Метод разложения на множители
2) Метод введения новой переменной
3) Функционально-графический метод.
4) Использование классических неравенств при решении олимпиадных задач
Рассмотрим данные методы более подробно.
Метод разложения на множители
Алгебраические уравнения и неравенства можно представить в виде P(x) = 0, P(x) ≤ 0 или P(x) ≥0 соответственно, где P(x) – многочлен. При решении алгебраических уравнений и неравенств зачастую приходится раскладывать многочлен на множители, то есть представлять его в виде произведения нескольких многочленов. Основным способам разложения многочлена на множители является применение формул сокращенного умножения, выделение полного квадрата, вынесение общего множителя, подбор корня многочлена по его старшему и свободному коэффициентам (следствие теоремы Безу).
|
|
|
Пример 1. Решите уравнение y - y 2-2 y 3= 
Р ешение.
Необходимо преобразовать уравнение таким образом, чтобы выделить куб суммы или разности двух выражений.
3 y - 3 y 2 - 6 y 3 -1 = 0,
y 3-3 y 2+3 y -1-7 y 3=0,
(y -1)3=7 y 3.
Извлечем корень кубический из правой и левой частей уравнения, получим
y - 1 = y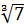 
, отсюда y =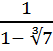 
Далеко не всегда многочлены имеют рациональные корни. В этом случае при разложении на множители приходится искать специальные способы – искусственные приемы: представление одного из слагаемых в виде суммы, прибавление и вычитание одного и того же выражения с целью последующей группировки, деление многочлена на многочлен (после отыскания корней по следствию из теоремы Безу).
Пример 2: Разложить на множители x4 +3x3 –x2-4x+2.
Целых корней многочлен не имеет (нужно проверить лишь делители числа 2).
Проведем группировку слагаемых: (x4+x3) + (2x3+2x2)+(-2x2-2x) –x2 -2x-2= x2(x2+x) +
+ 2x(x2+x)-2(x2+x) – (x2+2x-2) = (x2+x) (x2+2x-2)- (x2+2x-2)= (x2+2x-2) (x2+x-1)
Разложив на множители каждый из полученных квадратных трехчленов, придем к результату:
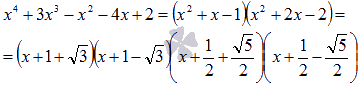Но, как бы нам не хотелось, некоторые многочлены (а точнее подавляющее большинство) так и не получится представить в виде произведения.
Пример 3:
Решите неравенство t 4-4 t 3+12 t 2-24 t +24<0
Решение.
| t 4 | - 4 t 3 | +12 t 2 - 24 t + 24 < 0 |
| t 4 | - 4 t 3 | + 4 t 2 - 4 t 2 +12 t 2 - 24 t + 24 < 0 |
(t 2-2 t)2+(8 t 2-24 t +24)<0.
Но (t 2 - 2 t)2 ³ 0 для любых t, а 8 t 2 - 24 t + 24 > 0 для любых t, так как
а>0, а дискриминант – отрицательный. Следовательно, все неравенство будет больше нуля.
Ответ: решений нет.
Метод введения новой переменной.
Суть метода:
1. В уравнении какая-то его часть заменяется другой переменной (a,y,t,...) (прежнее неизвестное одновременно с новым в уравнении быть не может);
|
|
|
2. Решается новое уравнение;
3. Возвращаются к обозначенному и, используя полученное число (корни), вычисляется требуемое неизвестное.
Но в уравнениях и неравенствах олимпиадного характера не всегда очевидно что надо заменять.
Решим уравнение:
+ 
- 
- 
- 
- 
+ 
+ 
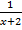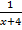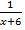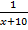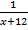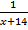= 0 Заменим: y = x+7
+ 
- 
- 
- 
- 
+ 
+ 
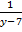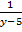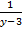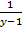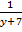= 0
+ + + - ( + ) – ( + ) = 0
+ 
- 
- 
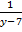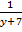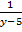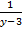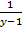= 0
2y (
+ 
- 
- 
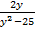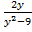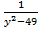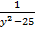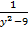) = 0
1) 2y = 0
y = 0 x = -7
2) 
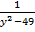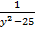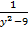+ - - = 0 
= z
+ 
- 
- 
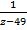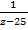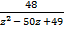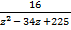= 0
+ 
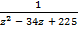= 0
+ 
= 0
3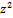 
– 102z + 675 + 
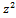– 50z + 49 = 0
4 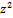– 152z + 724 = 0
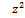- 38z + 181= 0
z = 19 ± 6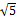 
y = ±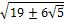 
x = -7 ± 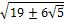Ответ: -7; -7 ± 
Здесь надо было заметить, что 7 – это число, относительно которого симметричны числа, стоящие в знаменателях исходного уравнения.
Функционально-графический метод.
Чаще всего функционально-графический метод применяют, когда в обеих частях
уравнения стоят функции разного вида.
Такое уравнение имеет вид f (x) = g (x)
Алгоритм функционально-графического метода заключается в следующем.
1. Правую и левую части уравнений f (x) и g (x) рассматривают как функции, входящие в уравнение.
2. В одной координатной системе строят графики функций у = f (x) и y = g (x).
Корнями уравнения будут являться абсциссы точек пересечения построенных графиков.
Пример 1.
Решите уравнение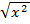 
+ 2x = 3,
[Всероссийская олимпиада по математике школьный этап 2012–2013 учебный год].
Упростим левую часть 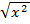+ 2x=|x| + 2x = -x+2x= x, если x< 0
x+2x=3x, если x >0
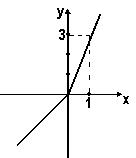
График будет такой:
Значение функции будет равно 3 при х= 1.
Ответ: 1.
|
|
|
