Композиция преобразований подобия.

Параллельный перенос.

 

Основания трапеции равны 4 см и 9 см, а диаго­нали равны 5 см и 12 см. Найти площадь трапеции и угол между ее диагоналями.

 

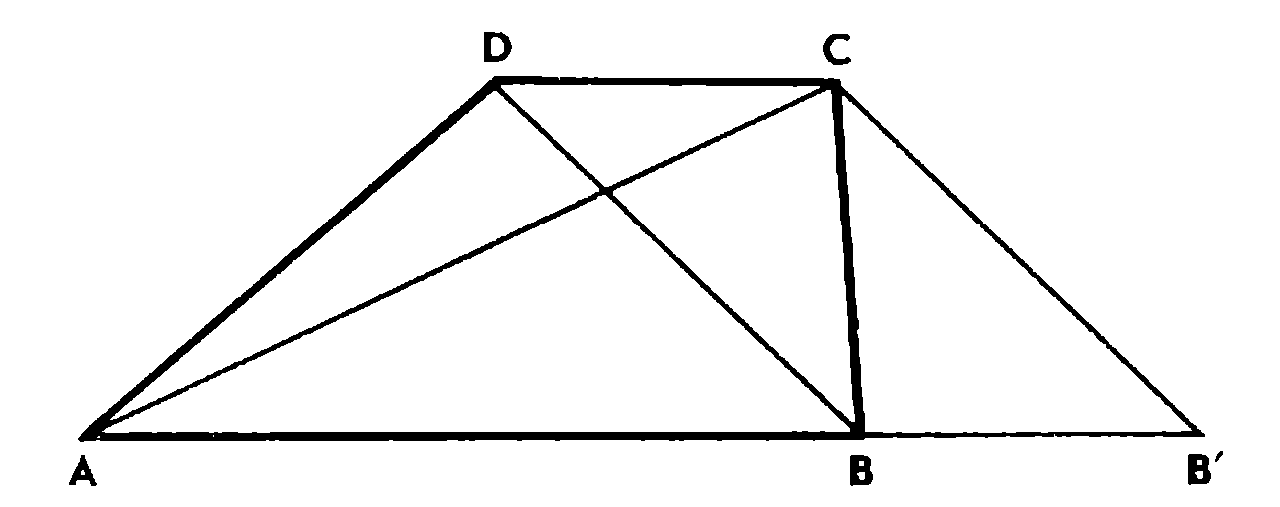
Решение. Пусть A BCD — данная трапеция, CD—-4 см, АВ — *д см, BD — 5 см и /4С = 12 см. Чтобы известные эле­менты включить в один треугольник, перенесем диагональ BD на

вектор DC в положение СВ'. Рассмотрим треугольник АСВ'. Так как В В'CD — параллелограмм, то В'С = BD = 5 см, АВ'~АВ-{- В В' — ЛВ-\- CD — 13 см.

Теперь известны все три стороны треугольника АВ'С, значит, можно найти его высоту, а затем и площадь трапеции.

Если же заметить, что площадь трапеции как раз и равна площади треугольника АВ'С (треугольники В В'С и A CD равно­велики), то решение задачи можно еще упростить.

Так как 5² + 12² = 13², то треугольник АВ'С прямоугольный.

Найдем его площадь: S = ^-* 12-5 = 30 см².

Итак, площадь трапеции равна 30 см². Угол между диагона­лями трапеции равен углу АСВ', значит, диагонали перпендику­лярны.

Аналогично решается задача на построение трапеции по основаниям и диагоналям: сначала строится вспомогательный треугольник, две стороны которого равны диагоналям, а третья — сумме оснований.

Заметим, что для вычисления площади трапеции и угла меж­ду диагоналями условие задачи можно было бы ослабить: вме­сто оснований трапеции задать только их сумму.

 

Центральная симметрия.

Доказать, что медиана треугольника меньше по­лусуммы заключающих ее сторон.

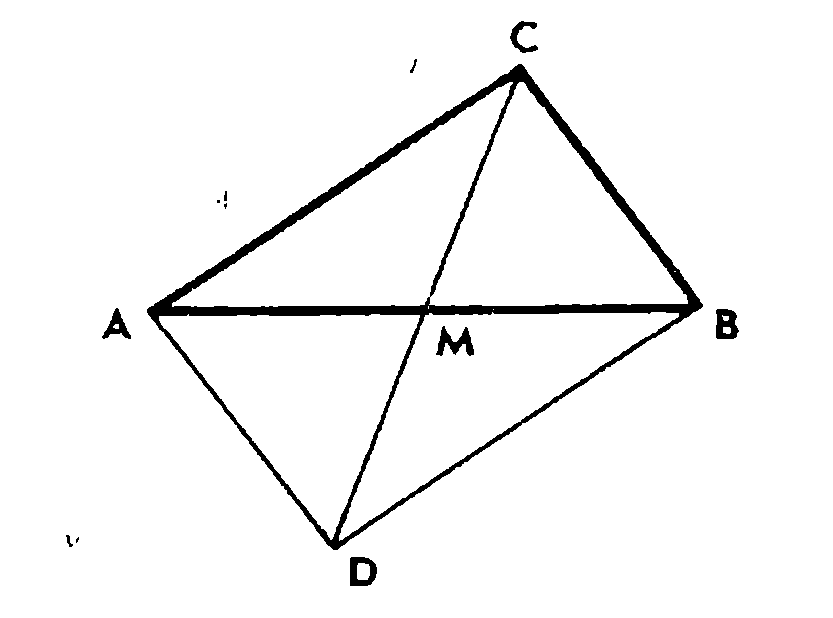
Решение. Пусть СМ — медиана треугольника ABC (рис. 8). Построим точку А, симметричную С относительно точки М. Так как М — середина отрезка АВ, то отрезок AD симметричен от­резку ВС. Мы получили треугольник ACD, в котором CD = 2СМ,

Следовательно, 2СМ <.АС + ВС, или т_с< ^а~^^Ь, где т_с = СМ,

а = ВС и Ь = АС.

С помощью такого же приема решается задача на построение треугольника ЛВС по двум сторонам и медиане, проведенной к третьей стороне, и некоторые другие задачи, в которых речь идет о медиане треугольника. Заметим, что ACBD — паралле­лограмм, поэтому указанный прием часто называют достраива­нием треугольника до параллелограмма.

Центральная симметрия обычно помогает решить задачу, когда фигура или часть фигуры имеет центр симметрии.

 

Поворот.

На сторонах АС и ВС произвольного треуголь­ника ABC вне его построены квадраты ACA_tA., и ВСВ_{В₂. Дока­зать, что отрезки ЛБ| и Л ,В равны и перпендикулярны.

 

Решение. Применим поворот вокруг точки С на 90°. Треугольники А,СА и ВСВ_{ равнобедренные прямо­угольные, поэтому при таком повороте точка А, перейдет в точку

А, точка В — в точку В_и отрезок A_tB — в отрезок АВ_{. Значит, эти отрезки равны и угол между ними равен углу поворота, т. е. 90°.

Примечание. Используя полученный результат, нетрудно доказать, что центры О и Р квадратов и середины М и М, отрез­ков АВ и А_]В₁ являются вершинами нового квадрата.

 

 

Композиция движений.

На сторонах АС и ВС произвольного треуголь­ника ЛВС вне его построены квадраты с центрами О и Р. Точка М — середина стороны АВ. Найти углы треугольника МОР.

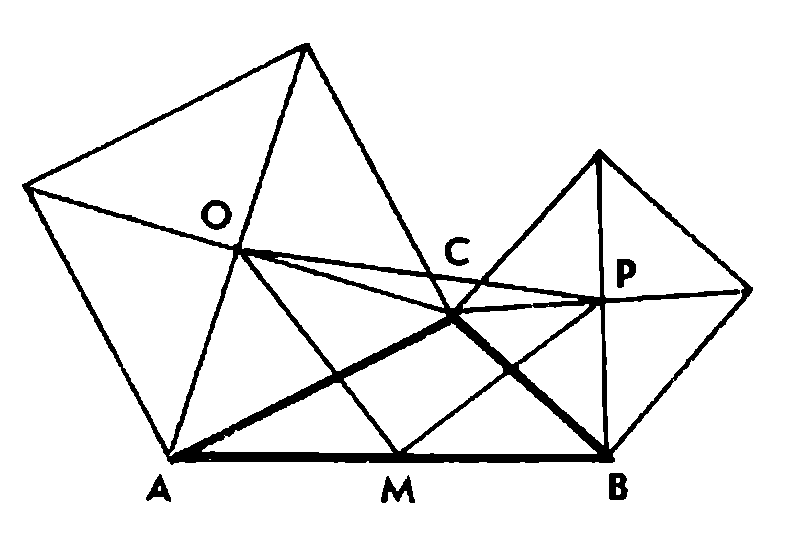
Решение. Для определенности, как и во всех последующих задачах, будем считать, что исходный треугольник ABC ориенти­рован положительно (рис. 15). Композиция F = R]^°° ° R^[p° ° R⁹q“ пе­реводит точку А в точку С, точку С в В, затем точку В снова в А, т. е. F(A) = A. Сумма углов поворота равна 360°. Значит, F — параллельный перенос с неподвижной точкой, т. е. тождествен­ное преобразование. Согласно теореме 3 углы треугольника ОРМ равны соответственно 45°, 45°, 90°.

Эту задачу можно решить также с использованием теорем элементарной геометрии и одного поворота. При­веденное решение более эффектив­но, а способ решения применим и к другим подобным задачам.

 

 

Преобразование подобия. Подобные фигуры.

Гомотетия и центрально-подобный поворот.

 

 

Композиция преобразований подобия.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: