 |
Индуктивный элемент (катушка индуктивности)
|
|
|
|
Условное графическое изображение катушки индуктивности приведено на рис. 2,а. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле.
Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки,
.
В свою очередь потокосцепление равно сумме произведений потока, пронизывающего витки, на число этих витков 
, где 
.
Основной характеристикой катушки индуктивности является зависимость 
, называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость представляет собой прямую линию, проходящую через начало координат (см. рис. 2,б); при этом
.
Нелинейные свойства катушки индуктивности (см. кривую на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для которого зависимость 
магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного гистерезиса нелинейная катушка характеризуется статической 
и дифференциальной 
индуктивностями.
Измерение индуктивности.
Неизвестная индуктивность Lх с известной электрической емкостью С образуют параллельный колебательный контур. На колебательный контур через резистор R от генератора подается напряжение синусоидальной формы частотой fг. Параллельно колебательному контуру подключается вольтметр V с большим входным сопротивлением, чтобы не шунтировать колебательный контур.
Контур C Lх имеет собственную (резонансную) частоту fо, которая определяется по формуле:
f2o=1/(LxC);
Изменяя частоту генератора fг по вольтметру V можно определить момент резонанса. При резонансе вольтметра V покажет максимальное значение напряжения на контуре, так как при резонансе fo = fг и контур будет иметь максимальное сопротивление. Зная резонансную частоту fo = fг, можно по формуле определить величину индуктивности:
|
|
|
Lx(мкГн)=2,53·1010/[f2o(кГц)C(пф)];
Мостовой метод измерения индуктивности.
В момент равновесия моста Z x Z 4= Z 2 Z 3, представленного комплексными числами, показание нульиндикатора равно нулю (Рис.30).
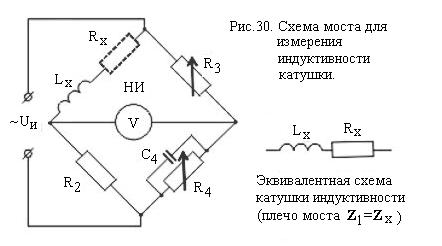
Из этого соотношения можно определить измеряемую индуктивность Lx.
Плечи моста в комплексном представлении будут иметь сопротивление:
Z x=Rх+iωLx; Z 2=R2; Z 3=R3; Z 4=R4/(1+iωR4С4);
Из условия равновесия моста Z x Z 4= Z 2 Z 3 будет справедливо равенство Z x= Z 2 Z 3/ Z 4, подставив значение плеч моста получим:
Rх+iωLx=R2R3(1+iωR4С4)/R4;
Учитывая,что R2,R3,С4, R4 величины известные и приравняв отдельно мнимые и действительные части равенства получим выражение определяющее величину измеряемой индуктивности:
Lx=R2R3С4; Rх=R2R3/R4;
От величины сопротивления Rх зависит добротность катушек. Чем больше величина сопротивления Rх тем лучше добротность катушки.
Q=ωLx/Rх=ωR4С4;
Добротность катушки Q, показывает во сколько раз активное сопротивление катушки ХL=ωLx меньше реактивного сопротивления - чем меньше сопротивление Rх тем меньше потерь в катушке. Измерение индуктивности катушки резонансным методом с небольшой добротностью становится проблематичной, так как при резонансе напряжение на контуре уменьшается и порой нельзя заметить повышение напряжения на контуре в момент резонанса.
Для оперативного измерения сопротивлений, индуктивностей, емкостей разработаны и выпускаются универсальные или специализированные мосты, магазины сопротивлений, и образцовые магазины индуктивностей и емкостей.
http://www.toehelp.ru/theory/toe/lecture01/lecture01.html
|
|
|
