 |
Нахождение характеристик дискретной случайной величины
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА 2 по ТЕОРИИ ВЕРОЯТНОСТЕЙ
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Моделирование закона распределения, математического ожидания и дисперсии
Элементы теории
Случайной называют величину, которая в результате испытания примет случайно одно и только одно значение из множества возможных значений.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения с определенными вероятностями.
Пример 1. Дискретной случайной величиной является число очков, выпавших при бросании игральной кости. Она принимает значения из дискретного числового множества M ={1, 2, 3, 4, 5, 6}.
Закон распределения
Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями (его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности:
| Х | х 1 | х 2 | ... | хn |
| P | p 1 | p 2 | ... | pn |
Сумма вероятностей второй строки таблицы равна единице:
p 1 + p 2 +...+ pn = 1.
Основные числовые характеристики дискретной случайной величины
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть дискретная случайная величина принимает только значения
x 1, x 2,..., xn, вероятности которых соответственно равны p 1, p 2,..., pn. Тогда математическое ожидание определяется равенством:
| M (X) = x 1 p 1 + x 2 p 2 +...+ xn pn. | (1) |
Пример 1. Найти математическое ожидание дискретной случайной величины, зная закон ее распределения:
|
|
|
| X | |||
| P | 0,2 | 0,5 | 0,3 |
Решение. По формуле (1) находим математическое ожидание:
M (X) = 5*0,2 + 4*0,5 + 3*0,3 = 3,3.
Если дискретная случайная величина принимает счетное множество возможных значений, то
M (X) = 
. (2)
На практике часто приходится оценить рассеяние возможных значений случайной величины вокруг ее среднего значения.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
| D (X) = M [ X - M (X)]2. | (3) |
Пример 2. Найти дисперсию случайной величины X, которая задана следующим законом распределения:
| X | |||
| P | 0,3 | 0,5 | 0,2 |
Решение. По формуле (1) находим математическое ожидание:
M (X) = 1*0,3 + 2*0,5 + 5*0,2 = 2,3.
Используя формулу (3) записываем все возможные значения квадрата отклонения:
[ X 1 - M (X)]2 = (1 - 2,3)2 = 1,69;
[ X 2 - M (X)]2 = (2 - 2,3)2 = 0,09;
[ X 3 - M (X)]2 = (5 - 2,3)2 = 7,29.
Тогда закон распределения квадрата отклонения имеет следующий вид:
| [ X - M (X)]2 | 1,69 | 0,09 | 7,29 |
| P | 0,3 | 0,5 | 0,2 |
По формуле (3) находим дисперсию:
D (X) = 1,69*0,3 + 0,09*0,5 + 7,29*0,2 = 2,01.
Для вычисления дисперсии часто бывает удобно пользоваться следующей формулой.
| D (X) = M (X 2) - [ M (X)]2 | (4) |
Пример 3. Найти дисперсию случайной величины X, которая задана следующим законом распределения:
| X | |||
| P | 0,3 | 0,5 | 0,2 |
Решение. По формуле (1) находим математическое ожидание:
M (X) = 2*0,1 + 3*0,6 + 5*0,3 = 3,5.
Закон распределения случайной величины X 2:
| X 2 | |||
| P | 0,1 | 0,6 | 0,3 |
Математическое ожидание М (Х 2):
M (Х 2) = 4*0,1 + 9*0,6 + 25*0,3 = 13,3.
По формуле (4) находим дисперсию:
D (X) = 13,3 - (3,5)2 = 1,05.
Средним квадратическим отклонением случайной величины Х называется корень квадратный из ее дисперсии:
σ (X) = 
.
Нахождение характеристик дискретной случайной величины
Аналитическое и непосредственное (на основе метода Монте-Карло) нахождение характеристик дискретной случайной величины рассмотрим на двух примерах.
|
|
|
Пример 4. На связке 5 ключей. при отмыкании замка последовательно один за другим испытываются ключи. Написать закон распределения числа испытанных ключей. Подсчитать математическое ожидание и дисперсию этой случайной величины.
Решение. Перенумеруем ключи. События Ai = «замок открывает i –й ключ»
(i = 1, 2, 3, 4, 5) независимы. Случайная величина X может принимать значения x 1 = 1, x 2 = 2, x 3 = 3, x 4 = 4, x 5 = 5.
Вероятность того, что замок откроется с 1-й попытки: p 1 = p (A 1) = 
= 0,2.
Событие, состоящее в том, что замок откроется со 2-й попытки, состоит из двух событий: 1-й ключ не открывает замок, 2-й открывает. Вероятность этого события:
p 2 = p (Ᾱ 1 A 2) = p (Ᾱ 1) · p (A 2/ Ᾱ 1) = 
· 
= = 0,2.
Событие, состоящее в том, что замок откроется с 3-й попытки, состоит из трех событий: 1-й ключ не открывает замок, 2-й – не открывает, 3-й открывает. Вероятность этого события:
р 3 = p (Ᾱ 1 Ᾱ 2 A 3) = p (Ᾱ 1) · p (Ᾱ 2/ Ᾱ 1) · p (A 3/ Ᾱ 1 Ᾱ 2) = · 
· 
= = 0,2.
Событие, состоящее в том, что замок откроется с 4-й попытки, состоит из четырех событий: 1-й ключ не открывает замок, 2-й – не открывает, 3-й – не открывает, 4-й открывает. Вероятность этого события:
р 4 = p (Ᾱ 1 Ᾱ 2 Ᾱ 3 A 4) = p (Ᾱ 1) · p (Ᾱ 2/ Ᾱ 1) · p (Ᾱ 3/ Ᾱ 1 Ᾱ 2) · p (A 4/ Ᾱ 1 Ᾱ 2 Ᾱ 3) =
= · · 
· 
= = 0,2.
Событие, состоящее в том, что замок откроется с 5-й попытки, состоит из пяти событий: 1-й ключ не открывает замок, 2-й – не открывает, 3-й – не открывает, 4-й – не открывает, 5-й – открывает. Вероятность этого события:
р 4 = p (Ᾱ 1 Ᾱ 2 Ᾱ 3 Ᾱ 4 A 5) = p (Ᾱ 1)· p (Ᾱ 2/ Ᾱ 1)· p (Ᾱ 3/ Ᾱ 1 Ᾱ 2)· p (Ᾱ 4/ Ᾱ 1 Ᾱ 2 Ᾱ 3)· p (A 5/ Ᾱ 1 Ᾱ 2 Ᾱ 3 Ᾱ 4) =
= · · · · 1 = = 0,2.
Таким образом, закон распределения числа испытанных ключей имеет вид:
| X | |||||
| P | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
Математическое ожидание:
M (X) = 1*0,2 + 2*0,2 + 3*0,2 + 4*0,2 + 5*0,2 = 3.
Закон распределения случайной величины X 2:
| X 2 | |||||
| P | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
Математическое ожидание М (Х 2):
M (Х 2) = 1*0,2 + 4*0,2 + 9*0,2 + 16*0,2 + 25*0,2 = 11.
Дисперсия:
D (X) = 11 – 32 = 2.
Пример 5. Монета подбрасывается 5 раз. Случайная величина Х - число выпавших гербов минус число выпавших цифр. Найти математическое ожидание и дисперсию этой случайной величины
Решение. Полную группу событий представляют собой следующие исходы опыта:
|
|
|
5 цифр, 0 гербов – x 0 = -5;
4 цифры, 1 герб – x 1 = -3;
3 цифры, 2 герба – x 2 = -1;
2 цифры, 3 герба – x 3 = 1;
1 цифра, 4 герба – x 4 = 3;
0 цифр, 5 гербов – x 5 = 5.
Пусть вероятность выпадения цифры р = , вероятность выпадения герба q = . Имеем обычную схему Бернулли: вероятность выпадения k цифр (5 – k гербов) в 5 подбрасываниях Pk (5) =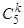 
pkq 5– k.
Таким образом, имеем:
P (X = –5) = P 5(5) = 
= 
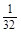; P (X = –3) = P 4(5) = 5· 
· 
= 
= 
;
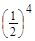P (X = –1) = P 3(5) =10·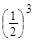 
· 
= 
; P (X =1) = P 2(5) = 10· · = 
= ;
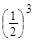P (X = 3) = P 1(5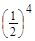) = 5· · = = ; P (X = 5) = P 0(5) = = .
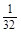Закон распределения числа выпавших гербов минус число выпавших цифр:
| X | -5 | -3 | -1 | |||
| P |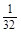
|
|
|
|
|
|
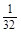
Математическое ожидание:
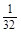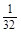M (X) = (-5)* + (-3)* + (-1)* + 1* + 3* + 5* = 0.
Закон распределения случайной величины X 2:
| X 2 | ||||||
| P |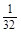
|
|
|
|
|
|
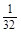
Математическое ожидание М (Х 2):
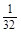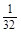M (Х 2) = 25* + 9* + 1* + 1* + 9* + 25* = 
= 5.
Дисперсия:
D (X) = 5 – 02 = 5.
Непосредственный подсчет характеристик дискретной случайной величины основан на методе Монте-Карло. С помощью датчика случайных чисел «разыгрывается» опыт, описанный в задаче. Исход опыта фиксируется. В результате многократного (n раз) повторения опыта получается частота ni его исходов. При этом n 1 + n 2 + … + nm = n, где m – число исходов. Разделив ni на n, i = 1, 2, …, m, получаем относительные частоты 
= pi ⃰, которые приблизительно равны значениям вероятности каждого исхода.
Сведя полученные результаты в таблицу
| Х | а 1 | а 2 | ... | am |
| P ⃰ | p 1⃰ | p 2⃰ | … | pm ⃰ |
где аi, i = 1, 2, …, m, – числовые значения исходов, получим приближенный закон распределения искомой случайной величины. В статистике эту таблицу называют распределением относительных частот.
Приближенным значением математического ожидания, или, как говорят в статистике, его оценкой, служит следующая величина
M ⃰ (X) = а 1 p 1⃰ + а 2 p 2⃰ +...+ аm pm ⃰ = 
(а 1 n 1 + а 2 n 2 +...+ аm nm).
Оценка (смещенная) дисперсии вычисляется по формуле
D ⃰ (X) = (а 1 – M ⃰ (X))*(а 1 – M ⃰ (X))* p 1⃰ + (аm – M ⃰ (X))*(аm – M ⃰ (X))* pm ⃰.
Программы (Pascal)
program kluchi;{На связке 5 ключей. при отмыкании замка последовательно один за другим испытываются ключи. Написать закон распределения числа испытанных ключей. Подсчитать математическое ожидание и дисперсию этой случайной величины}
|
|
|
const m=5;
Var
g,d:real;
i,n,u:integer;
ch: array [1..m] of integer;
ver: array [1..m] of real;
Begin
randomize;
writeln('vvedite n - chislo opytov');
read(n);
for i:=1 to n do {подсчет частоты}
Begin
u:=random(5);
ch[u+1]:=ch[u+1]+1;
end;
for i:=1 to m do {подсчет частоты}
ver[i]:=ch[i]/n;
writeln(' З А К О Н Р А С П Р Е Д Е Л Е Н И Я');
writeln;
writeln(' X ',' 1 2 3 4 5');
writeln(' P ',ver[1]:6:3,ver[2]:6:3,ver[3]:6:3,ver[4]:7:3,ver[5]:6:3);
g:=0;
for i:=1 to m do {подсчет мат. ожидания}
g:=g+i*ver[i];
d:=0;
for i:=1 to m do {подсчет дисперсии}
d:=d+((i-g)*(i-g))*ver[i];
writeln;
writeln(' n =',n:6,' mozh = ',g:4:3,' disp = ',d:4:3);
end.
Результаты
vvedite n - chislo opytov
З А К О Н Р А С П Р Е Д Е Л Е Н И Я
X 1 2 3 4 5
P 0.194 0.205 0.206 0.200 0.196
n = 10000 mozh = 3.000 disp = 1.963
program moneta;{монета подбрасывается 5 раз. Случайная величина Х - число выпавших гербов минус число выпавших цифр. Найти математическое
ожидание и дисперсию этой случайной величины}
const m=5;
Var
p,g,d:real;
s,i,j,k,n,u:integer;
ch: array [0..m] of integer;
ver: array [0..m] of real;
Begin
randomize;
p:=0.5;
writeln('vvedite n - chislo opytov');
read(n);
for i:=1 to n do
Begin
s:=0;{счетчик гербов}
for j:=1 to m do
if random <= p then s:=s+1;
for k:=0 to m do
if s=k then ch[k]:=ch[k]+1;
end;
for k:=0 to m do
ver[k]:=ch[k]/n;
writeln(' З А К О Н Р А С П Р Е Д Е Л Е Н И Я');
writeln;
writeln(' X ',' -5 -3 -1 1 3 5');
writeln(' P ',ver[0]:6:3,ver[1]:6:3,ver[2]:6:3,ver[3]:6:3,ver[4]:6:3,ver[5]:7:3);
g:=0;
for i:=0 to m do {подсчет мат.ож.}
g:=g+(2*i-5)*ver[i];
d:=0;
for i:=0 to m do {подсчет дисперсии}
d:=d+(2*i-5-g)*(2*i-5-g)*ver[i];
writeln;
writeln(' n =',n:6,' mozh = ',g:4:3,' disp = ',d:4:3);
end.
Результаты
vvedite n - chislo opytov
З А К О Н Р А С П Р Е Д Е Л Е Н И Я
X -5 -3 -1 1 3 5
P 0.031 0.157 0.313 0.312 0.156 0.032
n =1000000 mozh = 0.000 disp = 5.007
|
|
|
