V. Вывод формулы для определения момента инерции.

Лабораторная работа 14А

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ МЕТОДОМ ТРИФИЛЯРНОГО ПОДВЕСА

I. Цель работы: определение момента инерции твёрдых тел методом

трифилярного подвеса, проверка аддитивности момента инерции и теоремы Штейнера.

II. Приборы и принадлежности: трифилярный подвес, исследуемые тела, секундомер, штангенциркуль, измерительная линейка.

 

III. Краткая теоретическая часть.

При изучении вращательного, либо колебательного движений твердого тела используют понятие момента инерции. Моментом инерции твердого тела (либо системы тел) относительно некоторой оси называется физическая величина, равная сумме произведения масс материальных точек системы на квадрат их расстояний до оси вращения:

,

где n – число материальных точек, составляющих тело, либо систему тел.

В случае непрерывного распределения масс момент инерции может быть определен интегралом: 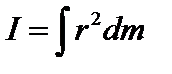, где r – функция положения точки массой dm.

Момент инерции зависит от массы тела и формы распределения массы относительно оси вращения.

Гармоническим крутильным колебанием тела называется периодическое движение относительно оси, проходящей через центр тяжести этого тела, когда угол отклонения от положе­ния равновесия изменяется по закону синуса или косинуса:

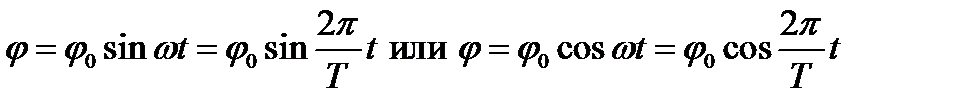, (1)

где j – угловое смещение, j₀ – максимальное угловое смещение,

– циклическая частота (угловая скорость), Т – период колебаний.

IV. Описание экспериментальной установки.

Рис. 1

Rr

j0a

l

h 1

h 2

l

r

r

BRr

A

На рис.1 показана принципиальная схема лабораторного прибора для определения момента инерции тела методом крутильных колебаний с помощью трифилярного подвеса. Трифилярный подвес состоит из диска массой Mрадиуса R, подвешенного на трёх симметрично расположенных металлических нитях. Наверху эти нити симметрично закреплены по краям диска меньшего радиуса r. При повороте верхнего диска на небольшой угол j₀ относительно вертикальной оси, перпендикулярной к плоскости диска и проходящей через его центр, все три нити принимают наклонное положение, центр тяжести системы несколько приподнимается по оси вращения. Нижний диск начинает совершать крутильные колебания, период которых будет зависеть от момента инерции системы. Эти колебания совершаются под действием момента сил, создаваемого силами натяжения. Под действием возвращающего момента сил нижний диск возвращается в положение равновесия, но по инерции проходит положение равно­весия и отклоняется от него в противоположную сторону. Затем всё повторяется вновь. Период колебаний определяется параметрами системы и характером распределением массы подвеса относительно оси вращения.

V. Вывод формулы для определения момента инерции.

Пусть при вращении диск поднялся, на высоту h =h₁ - h₂ (рис. 1). Тогда приращение потенциальной энергии равно

.

При опускании нижнего диска потенциальная энергия переходит в кинетическую энергию вращательного движения

,

где I₀ - момент инерции нижнего диска, w - угловая скорость диска.

В момент прохождения диском поло­жения равновесия угловая скорость w, а, следовательно, и кинетическая энергия, принимает максимальное значение, т.е. w = w₀.

Если пренебречь трением, то на основании закона сохранения энер­гии для колеблющегося диска можно записать: . (2)

Угловая скорость w, являющаяся первой производной от сме­щения j по времени, может быть записана

Максимальное значение угловой скорости равно: . (3)

На основании выражений (2) и (3) имеем: (4)

Найдем величину h при повороте диска на малый угол j₀, считая, что h₁ + h₂ » 2l:

. (5)

Из рис.1 ясно, что и .

Подставляя значение и в (5), получим:

.

Вследствие малости угла j₀ синус можно заменить аргумен­том: . (6)

Подставив выражения (3) и (6) в формулу (2), получим:

, или , (7)

где - постоянная установки.

Поделиться:

Воспользуйтесь поиском по сайту: