Графический метод решения задач линейного программирования

Образцы заданий к зачёту

 

1. Цех мебельного комбината выпускает комоды, трюмо и тумбочки. Норма расхода материала в расчете на одно изделие, плановая себестоимость, оптовая цена предприятия, плановый (месячный) ассортимент и трудоемкость единицы продукции приведены в таблице. Запас древесностружечных плит, досок еловых и березовых 120, 45 и 24 м³ соответственно. Плановый фонд рабочего времени 17500 человеко-часов.

 

Показатели	Комоды	Трюмо	Тумбочки
Норма расхода материала, м3 ДСП Доски еловые Доски березовые	0,041 0,019 0,005	0,028 0,022 0,004	0,034 0,010 0,006
Трудоемкость, чел.-час	11,2	7,2	6,1
Плановая себестоимость, тыс. руб.	3,6	3,1	2,7
Оптовая цена предприятия, тыс. руб.	4,8	4,2	3,6
Плановый ассортимент, шт.

 

Исходя из необходимости выполнения плана по ассортименту и возможности его перевыполнения по отдельным (или даже по всем) показателям построить модель, на основе которой можно сформулировать задачу максимизации прибыли.

 

 

2. Решить задачу графическим методом

 

3. Имеется три склада и три магазина. На складах имеется груз в количестве 75, 40 и 35 ед. соответственно. Потребность магазинов составляет соответственно 55, 45 и 50 ед. Стоимости перевозок от каждого склада к каждому магазину составляют:

 

 

Найти такой план перевозок, чтобы общая стоимость всех перевозок была минимальной.

 

Методические указания

Графический метод решения задач линейного программирования

 

Наиболее простым и наглядным методом линейного программирования (ЛП) является графический метод. Он применяется для решения задач ЛП с двумя переменными.

Рассмотрим задачу ЛП в стандартной форме записи:

Положим n=2, т. е. рассмотрим эту задачу на плоскости. Пусть система неравенств совместна (имеет хотя бы одно решение).

Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости. Определим, какую часть плоскости описывает неравенство 2х₁+3х₂£ 12. Во-первых, построим прямую 2х₁+3х₂=12. Эта прямая проходит через точки (6, 0) и (0, 4). Для того чтобы определить, какая полуплоскость удовлетворяет неравенству необходимо выбрать любую точку на графике, не принадлежащую прямой, и подставить ее координаты в неравенство. Если неравенство будет выполняться, то данная точка является допустимым решением и полуплоскость, содержащая точку, удовлетворяет неравенству. Удобной для использования при подстановке в неравенство является начало координат. Подставим x₁=x₂=0 в неравенство 2х₁+3х₂£12. Получим 2´0+3´0£12. Данное утверждение является верным, следовательно, неравенству 2х₁+3х₂£12 соответствует нижняя полуплоскость, содержащая точку (0.0). Это отражено на графике, изображенном на рисунке.

Аналогично можно изобразить графически каждое ограничение задачи линейного программирования.

Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, образует выпуклое множество и называется областью допустимых решений или областью определения. Необходимо помнить, что область допустимых решений удовлетворяет условиям неотрицательности (x_j³0, j=1,…,n). Координаты любой точки, принадлежащей области определения являются допустимым решением задачи. Таким образом, геометрически задача линейного программирования (ЗЛП) представляет собой отыскание такой точки многоугольника решений, координаты которой доставляют целевой функции максимальное (минимальное) значение.

Для нахождения экстремального значения целевой функ­ции при графическом решении задач ЛП используют вектор–градиент, координаты которого являются частными производными целевой функции, т. е.

.

Этот вектор показывает направление наискорейшего изменения це­левой функции. Прямая , перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине “a”. Меняя значение “a”, получим семейство параллельных прямых, каждая из которых является линией уровня.

Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – убывает.

С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Графический метод решения ЗЛП состоит из следующих этапов.

1. Строится многоугольная область допустимых решений ЗЛП – ОДР,
2. Строится вектор-градиент ЦФ в какой-нибудь точке Х₀ принадлежащей ОДР – .
3. Линия уровня C₁x₁+C₂x₂ = а (а –постоянная величина) - прямая, перпендикулярная вектору–градиенту – передвигается в направлении этого вектора в случае максимизации f (x_1,x₂) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x_1,x₂).
4. Для нахождения ее координат достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x_1,x₂), найденное в получаемой точке, является максимальным.

При минимизации f(x_1,x₂) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то соответствующий максимум или минимум f(x_1,x₂) не существует.

Если линия уровня параллельна какому-либо функциональному ограничению задачи, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.

 

 

Рассмотрим графическое решение задач линейного программирования на следующем примере.

Задача. о планировании выпуска продукции пошивочного предприятия. (Задача о костюмах).

Намечается выпуск двух видов костюмов - мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм - 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 человеко-дней трудозатрат. Требуется определить, сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского - 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.

Модель задачи.

Введем следующие обозначения: х₁ - число женских костюмов; x₂ - число мужских костюмов.

Прибыль от реализации женских костюмов составляет 10х₁, а от реализации мужских 20х₂, т.е. необходимо максимизировать целевую функцию

f(x) = 10 х₁ + 20 х₂ -> max.

Ограничения задачи имеют вид:

х₁ + х₂ £ 150

2 х₁ + 0.5 х₂ £ 240

х₁ + 3.5 х₂ £ 350

х₂³ 60

х₁ ³ 0

Первое ограничение по труду х₁ + х₂ £ 150. Прямая х₁ + х₂ = 150 проходит через точки (150, 0) и (0, 150).

Второе ограничение по лавсану 2 х₁ + 0.5 х₂ £ 240. Прямая 2 х₁ + 0.5 х₂ = 240 проходит через точки (120, 0) и (0, 480).

Третье ограничение по шерсти х₁ + 3.5 х₂ £ 350. Прямая х₁ + 3.5 х₂ = 350240 проходит через точки (350, 0) и (0, 100).

Добавим четвертое ограничение по количеству мужских костюмов х2 ³ 60. Решением этого неравенства является полуплоскость, лежащая выше прямой х2 = 60. На рис.2. заштрихована область допустимых решений.

Для определения направления движения к оптимуму построим вектор-градиент Ñ, координаты которого являются частными производными целевой функции, т.е. = (10;20). Чтобы построить этот вектор, нужно соединить точку (10;20) с началом координат. При максимизации целевой функции необходимо двигаться в направлении вектора-градиента, а при минимизации — в противоположном направлении. Для удобства можно строить вектор, пропорциональный вектору Ñ.

В нашем случае движение линии уровня будем осуществлять до ее выхода из области допустимых решений. в крайней, угловой точке достигается максимум целевой функции. Для нахождения координат этой точки достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума:

х₁ + 3.5 х₂ = 350

х₁ + х₂ = 150.

Отсюда легко записать решение исходной ЗЛП: max f(x) = 2300 и достигается при x₁=70 и x₂=80.

Транспортная задача

 

Пусть имеется m поставщиков А ₁, А ₂,..., А_m однородного груза в количествах соответственно а ₁, а ₂,..,. а_m единиц и n потребителей В ₁, В ₂,..., В_n этого груза, потребность которых составляет соответственно b ₁, b ₂..., b_n единиц.

Известны стоимости перевозок (тариф) единицы груза от i -го поставщика к j -му потребителю - с_ij (i=1,m; j=1,n).

Требуется составить такой план перевозок, который обеспечит минимальные транспортные расходы.

Возможны три ситуации:

1) количество груза у всех поставщиков равно потребности в данном грузе всех потребителей:

или .

2) количество груза у всех поставщиков больше потребности в данном грузе всех потребителей:

или .

3) количество груза у всех поставщиков меньше потребности в данном грузе всех потребителей:

или .

В первом случае модель задачи называется закрытой, во втором и третьем – открытой.

Теорема. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство .

В случае превышения запаса над потребностью вводится фиктивный (n + 1)-й пункт назначения с потребностью и соответствующие тарифы считаются равными нулю.

Аналогично вводится фиктивный (m + 1)-й пункт отправления с запасом груза и тарифы полагаются равными нулю. Этим задача сводится к закрытой транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи.

Решение транспортной задачи включает следующие этапы:

1. Нахождение первоначального опорного плана (метод северо-западного угла, метод минимальной стоимости). При этом число заполненных клеток должно быть равно m + n - 1.

При нахождении опорного плана методом северо-западного угла запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.

Заполнение начинается с левой верхней клетки (северо-западный угол). На каждом шаге, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и исключается из рассмотрения один поставщик или потребитель. Если в очередную клетку таблицы требуется поставить перевозку, а поставщик или потребитель имеют нулевые запасы или запросы, то в клетку ставится перевозка, равная нулю (базисный нуль), и после этого исключается из рассмотрения поставщик или потребитель.

Метод минимальной стоимости позволяет построить решение, близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи. На каждом шаге заполняется только одна клетка, соответствующая минимальной стоимости, и исключается из рассмотрения только один поставщик или один потребитель. Очередную клетку, соответствующую минимальной стоимости, заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы исчерпаны полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения.

2. Проверка опорного плана на оптимальность, например, методом потенциалов.

 

Пример. Четыре предприятия используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 100, 90, 170 и 30 ед. Сырьё сосредоточено в трёх пунктах, а запасы соответственно равны 200, 160, и 140 ед. Тарифы перевозок заданы матрицей

.

 

Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.

Данная задача является открытой, так как потребности в сырье 100+90+170+30=390 меньше запасов 200+160+140=500. Введём 5-го фиктивного потребителя с потребностью .

Теперь исходные данные задачи запишем в виде таблицы, а опорный план получим методом северо-западного угла.

Заполнение таблицы начинаем с клетки (1, 1). х ₁₁ = min(a ₁=200, b ₁=100)= b ₁=100 – запасы А ₁ позволяют полностью удовлетворить потребности пункта В1, значит исключаем этого потребителя из рассмотрения. Теперь запасы пункта A ₁ считаем равными a ₁=200 - 100=100 ед. В оставшейся части таблицы левой верхней клеткой является (1, 2): х ₁₂= min(a ₁, b ₂)= b ₂=90 – снова запасы удовлетворяют потребность полностью. Внесём значение в соответствующую клетку и исключим из рассмотрения столбец В ₂. Запасы пункта А ₁ считаем равными a ₁ = 100 – 90 = 10 ед. Теперь «северо-западным углом» является клетка (1, 3). х ₁₃ = min(a ₁, b ₃)= a ₁ =10 – запасы могут удовлетворить потребность пункта B ₃ частично. Заполняем клетку (1, 3) и исключаем из рассмотрения строку A ₁. Потребности пункта B ₃ считаем равными b ₃ = 170 - 10 = 160. х ₂₃ = min(a 2, b 3) = a ₂ = b ₃ = 160 – запасы A ₂ исчерпаны, потребность B ₃ удовлетворена. Но по правилам мы не можем вычеркнуть и строку и столбец одновременно. Поэтому исключим из рассмотрения сначала столбец B ₃, а в клетку (2, 4) запишем х ₂₄ = 0 (так как запасы А ₂ уже исчерпаны) и только теперь вычеркнем строку А ₂. И так далее. Получим следующую таблицу.

 

Потребности   Запасы	b 1=100	b 2=90	b 3=170	b 4=30	b 5=110
β1=12	β2=15	β3=21	β4=16	β5=4
a 1=200	α1=0	12 100	15 90	21 10
a 2=160	α2=-6			15 160	10 0
a 3=140	α3=-4				12 30	0 110

 

Число заполненных клеток равно 7 и m + n - 1=3 + 5 – 1 = 7 – план невырожденный. Оптимальный план найдём методом потенциалов.

Теорема. В оптимальном плане транспортной задачи заполненным клеткам отвечают равенства , а пустым неравенства .

Расставим потенциалы:

, положим , тогда .

(Обычно равным нулю принимают потенциал строки или столбца с наибольшим числом заполненных клеток.)

Теперь проверим пустые клетки на выполнение неравенства .

.

Для клеток (1, 4), (1, 5), (2, 2) неравенство не выполняется, значит опорный план не является оптимальным. В одну из этих клеток нужно "ввезти" груз. Выбираем ту, для которой разница максимальна, т. е. в (1, 5). Строим цикл.

Цикл перерасчёта таблицы - это последовательность ячеек, начинающаяся и заканчивающаяся в одной и той же клетке, с вершинами, лежащими в занятых клетках, кроме одной.

Вершина цикла – клетка, в которой происходит поворот под прямым углом.

"Перемещаем" груз по следующим правилам:

1. каждой из клеток, связанных циклом присваивается знак: пустой ячейке " + ", остальным - поочерёдно знаки " - " и " + ".

2. среди минусовых клеток находим число 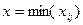и прибавляем его к числам, стоящим в плюсовых клетках, и вычитаем из чисел, стоящих в минусовых клетках; остальные клетки вне цикла остаются без изменения.

В нашем примере цикл образуют шесть ячеек: (1, 5) – пустая, для которой не выполняется неравенство, и (3, 5), (3, 4), (2, 4), (2, 3), (1, 3) – заполненные.

 

х = min (10,0,110)=0. Значит в плюсовые клетки "завозим" 0 ед. груза, из минусовых "вывозим". Получим новый опорный план:

 

Потребности   Запасы	b 1=100	b 2=90	b 3=170	b 4=30	b 5=110
β1=12	β2=15	β3=21	β4=12	β 5=0
a 1=200	α1=0	12 100	15 90	21 10		0 0
a 2=160	α2=-6			15 160
a 3=140	α3=0				12 30	0 110

 

Расставим потенциалы и проверим пустые клетки на выполнение неравенства . Для клетки (2,2) неравенство не выполняется. Строим новый цикл.

 

х = min (90,160)=90. Значит в плюсовые клетки "завозим" 90 ед. груза, из минусовых "вывозим". Получим новый опорный план:

 

Потребности   Запасы	b 1=100	b 2=90	b 3=170	b 4=30	b 5=110
β1=12	β2=14	β3=21	β4=12	β 5=0
a 1=200	α1=0	12 100		21 100		0 0
a 2=160	α2=-6		8 90	15 70
a 3=140	α3=0				12 30	0 110

 

Расставим потенциалы и проверим пустые клетки на выполнение неравенства . Полученный план является оптимальным.

Ответ: ,

=100*12+100*21+90*8+70*15+30*12=5430.

Так как пятый потребитель является фиктивным, то 110 ед. груза у третьего поставщика останутся невостребованными.

Поделиться:

Воспользуйтесь поиском по сайту: