Общие сведения об однократных измерениях

ЛАБОРАТОРНАЯ РАБОТА №1

ОДНОКРАТНЫЕ ИЗМЕРЕНИЯ ПРИБОРАМИ ОБЩЕГО НАЗНАЧЕНИЯ

Время работы – 4 часа

ЦЕЛЬ РАБОТЫ:

2. Изучить правила применения измерительных приборов общего назначения (мультимеры, тестеры, милливольтметры).

3. Закрепить знания методик проведения однократных прямых и косвенных измерений и оформления результатов наблюдения.

 

ЗАДАНИЕ НА ПОДГОТОВКУ К ПРОВЕДЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ

Изучить (по конспектам лекций и рекомендованной литературе) теоретический материал «Основы теории погрешностей», практических занятий 8/1 и 8/2 «Изучение устройств, характеристик и правил пользования приборами UIR общего назначения», а также краткие теоретические сведения (настоящая работа).

Допуск к лабораторной работе проводится в виде письменной работы с ответами на контрольные вопросы или в виде теста на ПЭВМ.

Изучить по данному руководству порядок выполнения работы и подготовить структуру отчета с указанием наименования работы, целей работы, пунктов экспериментальных исследований. На рабочую подгруппу в день выполнения работы должен быть подготовлен хотя бы один отчет. В каждом пункте исследований привести схемы измерений, таблицы, координатные оси для построения графиков (масштабы выбирают­ся исполнителем), Оставить место для расчетов и выводов.

В день выполнения работы группа может выполнять защиту по одному отчету, в последующие дни – по индивидуальным отчетам.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Статистическая обработка результатов однократных, совместных

И измерений

Общие сведения об однократных измерениях

Прямые однократные измерения являются наиболее распространенными. В производственных условиях их точность часто оказывается вполне прием­лемой, а простота выполнения, высокая производительность (количество измерений в единицу времени) и низкая стоимость ставят однократное изме­рение вне конкуренции с любыми другими. Однако эти измерения возможны лишь при следующих условиях:

• объем априорной информации об объекте измерении такой, что аналитическая модель объекта и определение измеряемой величины не вызывают сомнений;

• метод измерения достаточно изучен, и его погрешности либо заранее
устранены, либо оценены;

• средства измерений исправны, а их метрологические характеристики
соответствуют установленным нормам.

Методика обработки результатов прямых однократных измерений указана в соответствующих нормативных документах, посвященных прямым однократным измерениям и оцениванию погрешностей результатов измерений. Применение методики возможно, если известны составляющие погрешности измерения, закон распределения случайных составляющих — нормальный, а неисключенных сис­тематических погрешностей (НСП) — равномерный с известными границами .

Результатом прямого однократного измерения физической величины является показание, снятое непосредственно с используемого средст­ва измерения. До измерения должна быть проведена априорная оценка составляющих погрешности с использованием всех доступных данных. При определении доверительных границ погрешности результата измерений до­верительная вероятность принимается, как правило, равной 0,95.

Погрешность результата прямого однократного измерения включает погрешность средства измерения (инструментальную погрешность), погреш­ность использованного метода и субъективную (личную) погрешность опера­тора. Каждая из этих составляющих может иметь неисключенные системати­ческие погрешности и случайные.

Оценивание погрешностей прямых однократных измерений можно под­разделить на точное и приближенное.

Прямые однократные измерения с точным оцениванием погрешностей выполняются по специальной методике, определенной нормативными документами, в случаях важности измерений. Содержание методики можно найти, например в [1], c. 119 – 120.

1.2. Прямые однократные измерения с приближенным оцениванием погрешностей

При таком подходе необходимо перед началом измерений провести предварительную оценку составляющих погрешности результата измерения и собственно погрешности измерения. Эта информация извлекается из опыта проведе­ния подобных измерений, из нормативно-технической документации на используемые средства измерений, из научно-технических отчетов и дру­гих источников. Если априорная оценка погрешности превышает допустимую, то следует выбрать более точное средство измерений или изменить методи­ку измерения.

Допускается пренебрежение случайными погрешностями, если доказано, что граница неисключенных систематических погрешностей результата измере­ния больше оценки СКО случайных погрешностей в восемь раз и более.

В простейшем случае погрешность результата измерения не превышает предела допускаемой абсолютной основной погрешности средства измерения , оп­ределяемой по нормативно-технической документации, если измерения про­водились в нормальных условиях. При этом результат измерения можно за­писать в виде , т. е. без указания доверительной вероятности, ко­торая подразумевается равной = 0,95. Если же измерения проводились в условиях, отличающихся от нормальных, то следует определять и учитывать пределы дополнительных погрешностей, а затем суммировать их с основны­ми погрешностями. Порядок такого суммирования приведен в нормативных метрологических документах.

Пример 5. Оценить результат и погрешность однократного измерения значения напряжения на участке электрической цепи сопротивлением R = 4 Ом, выполненного вольтметром класса точности 0, 5 % с верхним пределом измерения = 1,5 В и внутренним сопротивлением 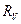= 1000 Ом. Показание вольтметра = 0,90 В. Из­вестно, что дополнительные относительные погрешности показаний вольтметра из-за влияния магнитного поля и окружающей температуры не превышают соответственно значений и допускаемой предельной относительной погрешности.

Инструментальная составляющая погрешности измерения опреде­ляется основной и дополнительной погрешностями. При показании вольтметра 0,90 В предел допускаемой относительной погрешности вольтметра на этой отметке в процентах равен:

.

Методическая погрешность определяется соотношением между сопротивлением участка цепи R и сопротивлением вольтметра При подсоединении вольтметра исходное напряжение U_x изменится из-за наличия сопротивления 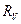и составит:

Отсюда относительная методическая погрешность:

.

Эта методическая погрешность является систематической и должна быть исключена из результата измерения путем введения поправки:

С = 0,90·0,4/100 = 0,004 В.

Тогда результат измерения с учетом поправки на систематическую погрешность:

0,90 В + 0,004 В = 0,904 В.

Относительная погрешность результата измерения находится суммированием

= 0,83 + 0,75 + 0,3= 1,88 %.

Переходя к абсолютной суммарной погрешности, получим

В.

Применив статистическое суммирование при доверительной вероятности 0,95, получим значение доверительной границы неисключенных систе­матических погрешностей:

.

Находим абсолютную погрешность:

Округляя, окончательный результат измерения можно представить в форме:

Косвенные измерения

При косвенных измерениях физическая величина А, значение которой на­до измерить, является известной функцией ряда других величин — аргу­ментов Данные аргументы подвергаются прямым измере­ниям, а величина А вычисляется по формуле:

(1.1)

В качестве результата косвенного измерения рассматривают оценку ве­личины А, определяемую подстановкой в представленную функциональную связь оценок аргументов этой функции. Каждый из аргументов измеряется с некоторой погрешностью, вносящей определенный вклад в результат косвенного измерения.

Этот вклад зависит от вида функциональной зависимости (1.1). С учетом этого вида все косвен­ные измерения подразделяют на линейные и нелинейные. К линейным кос­венным измерениям относятся только те, когда функция (1.1) представляет собой сумму из т составляющих вида где — некоторое число. При любом другом виде функции косвенные измерения относятся к нели­нейным.

При нелинейных косвенных измерениях обычно проводят приближенную оценку погрешности результата косвенного измерения на основе линеариза­ции функции (1.1).

Методика обработки результатов косвенных линейных измерений стандартизирова­на. Не вдаваясь в ее подробности отметим, что оцен­ку СКО случайной погрешности результата косвенного линейного измерения в зависимости от оценок СКО случайных погрешностей аргументов в общем случае можно определить по формуле:

где — оценка коэффициента корреляции, определяющего меру статисти­ческой связи случайных величин и Все возможные значения оценки ко­эффициента корреляции лежат в интервале от - 1 до + 1. Установление значения обычно затруднительно. Поэтому рассматривают два случая: (полная статистическая связь между аргументами) и 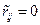(отсутствие связи). При =0 оценку СКО вычисляют по формуле:

(1.2)

Для использования выражений (1.2) требуется вычисление оце­нок СКО аргументов функции (1.1) на основе обработки результатов их многократных наблюдений.

Интересны частные случаи вычисления СКО косвенного измерения при отсутствии корреляции между погрешностями измерения аргументов.

Пусть функция (1.1) имеет вид суммы, или если наблюдается зависимость от одного аргумента:

(1.3)

Найдя ее частные производные 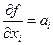и подставив их в (1.2), получим:

. . (1.4)

Предположим, что функция (1.1) имеет вид произведения:

(1.5)

где k, — константы. Определим ее частные производные по аргу­ментам х₁, х₂,..., х_т и подставим их в (1.5). После простых преобразований получим удобное для расчетов выражение:

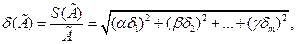(1.6)

где — соответственно относительные СКО случайных погрешностей результата измерения и i -го аргумента.

Отметим важные выводы и замечания:

1. Если результат косвенных измерений равен взвешенной сумме прямых измерений (см. 1.3), то дисперсия результата измерений равна сумме квадратов взвешенных СКО прямых измерений (см. 1.4).

2. Если определяется погрешность суммы двух (и более) независимых измерений, то дисперсиясуммарного измерения равна сумме дисперсий каждого из измерений

3. Если определяется погрешность произведения двух (и более) независимых измерений, то относительная дисперсиясуммарного измерения равна сумме взвешенных в квадрате (см.1.6) относительных дисперсий каждого из измерений. Величины последних часто можно определить из паспортных данных измерительного прибора.

4. При очень приближенном оценивании, (а также когда нет возможности набрать статистику и определить дисперсию каждого их прямых наблюдений), вместо СКО прямых наблюдений можно использовать предел допускаемой абсолютной погрешности измерений.

5. Для косвенных измерений могут быть определены доверительные границы случайной погрешности и неисключенных систематических погрешностей. Методика процедуры может быть найдена в соответствующих ГОСТах. Результат косвенного измерения и его погрешность должны представляться в виде формулы:

.

В заключение отметим, что при однократных измерениях аргументов процедура определения результата косвенно измеряемой величины сохраняется такой же, как и при многократных измерениях.

Пример. Оценка мощности, рассеиваемой на резисторе, проводилась по формуле:

Прямые измерения проведены в нормальных условиях цифровым мультиметром при времени преобразования Результаты измерений =758,8 мВ, 5,3 кОм, 1,5 мВ, 0,015кОм. Результаты измерений не коррелированны. Измерения напряжения проводились по шкале 1000 мВ, при этом для цифрового мультиметра

Определить и записать результаты измерения мощности при доверительной вероятности

Решение: Для исходных данных вычисляем измеряемое значение мощности

мкВт.

Определяем относительную систематическую погрешность измерения по формуле:

*

Вычисляем погрешности и по паспортным данным исследуемого мультиметра:

Полученные значения и подставляем в выражение (*) для относительной систематической погрешности измерения мощности и находим:

Переходя к абсолютной погрешности, получаем:

мкВт.

Результат измерения мощности записываем в виде:

мкВт;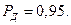

 

Справочные сведения

Погрешности измерений

Абсолютная погрешность D - отклонение результата измерения от истинного значения (выражается в единицах измеряемой величины).

Относительная погрешность d - отношение абсолютной погрешности измерения к истинному (или измеренному) значению измеряемой величины, часто выражается в процентах: или .

Приведенная погрешность g - отношение абсолютной погрешности D к конечному значению шкалы прибора (или к сумме шкал при двусторонней шкале).

Систематическая погрешность D_с – погрешность, закономерно появляющаяся при многократных измерениях (всегда подлежит устранению).

Случайные погрешности - существуют всегда, учитываются в процессе статистической обработки.

Грубые погрешности (промахи) – подлежат исключению из результатов наблюдения.

Основная погрешность имеет место при нормальных условиях эксплуатации прибора, оговоренных в регламентирующих документах.

Дополнительная погрешность возникает при выходе какой-либо из влияющих величин за пределы нормальной области значений.

Класс точности средства измерения – обобщенная характеристика средства измерения, характеризующая его свойства в отношении точности, но не являющаяся непосредственным показателем точности измерений, выполненных с помощью этого средства.

 

Поделиться:

Воспользуйтесь поиском по сайту: