 |
Уравнение напряжения и тока асинхронного двигателя
|
|
|
|
2.5. Процессы в асинхронной машине
2.5.1. Цепь статора
А) ЭДС статора.
Магнитное поле, создаваемое обмоткой статора, вращается относительно неподвижного статора с частотой n 0=60 f)/ p и будет наводить в обмотке статора ЭДС. Действующее значение ЭДС, наводимой этим полем в одной фазе обмотки статора определяется выражением:
E 1=4,44 w 1 k 1 f Φ,
где: k 1=0.92÷0.98– обмоточный коэффициент;
f 1= f – частота сети;
w 1– число витков одной фазы обмотки статора;
Φ – результирующее магнитное поле в машине.
Б) Уравнение электрического равновесия фазы обмотки статора.
Это уравнение составлено по аналогии с катушкой с сердечником, работающей на переменном токе.
.
Здесь Ú и Ú1– напряжение сети и напряжение, подведённое к обмотке статора.
R 1– активное сопротивление обмотки статора, связанное с потерями на нагрев обмотки.
x 1– индуктивное сопротивление обмотки статора, связанное с потоком рассеяния.
z 1– полное сопротивление обмотки статора.
İ1– ток в обмотке статора.
При анализе работы асинхронных машин часто принимают I 1 z 1=0. Тогда можно записать:
U 1≈ E 1=4,44 w 1 k 1 f Φ.
Из этого выражения следует, что магнитный поток Φ в асинхронной машине не зависит от её режима работы, а при заданной частоте сети f зависит только от действующего значения приложенного напряжения U 1. Аналогичное соотношение имеет место и в другой машине переменного тока – в трансформаторе.
Цепь ротора
А) Частота ЭДС и тока ротора.
При неподвижном роторе частота ЭДС f 2равна частоте сети f.
f 2= f =(n 0 p)/60.
При вращающемся роторе частота ЭДС ротора зависит от частоты вращения магнитного поля относительно вращающегося ротора, которая определяется соотношением:
|
|
|
n' = n 0− n.
Тогда частота ЭДС вращающегося ротора:
.
Частота ЭДС ротора изменяется пропорционально скольжению и в режиме двигателя имеет наибольшее значение в момент пуска в ход.
Пусть при f =50Гц, номинальное скольжение S н=2%. Тогда при номинальной частоте вращения ротора f 2= f × S н=1Гц.
Таким образом, в обмотке ротора асинхронной машины частота наводимой ЭДС зависит от частоты вращения ротора.
Б) ЭДС ротора.
При неподвижном роторе f 2= f и действующее значение ЭДС определяется по аналогии с E 1.
E 2=4,44 w 2 k 2 f Φ,
где: w 2и k 2– соответственно число витков и обмоточный коэффициент обмотки ротора.
Если ротор вращается, то f 2= f × S ни ЭДС вращающегося ротора определяется соотношением:
E 2 S =4,44 w 2 k 2 f 2Φ= E 2 S.
ЭДС, наводимая в обмотке ротора, изменяется пропорционально скольжению и в режиме двигателя имеет наибольшее значение в момент пуска в ход.
Отношение ЭДС статора к ЭДС неподвижного ротора называется коэффициентом трансформации асинхронной машины.
| k = | E 1 | = | w 1 k 1 | . |
| E 2 | w 2 k 2 |
В) ток ротора.
Запишем уравнение равновесия для одной фазы короткозамкнутого ротора.
При неподвижном роторе.
,
где: x 2=2π fL 2– индуктивное сопротивление обмотки неподвижного ротора, связанное с потоком рассеяния;
R 2– активное сопротивление обмотки ротора, связанное с потерями на нагрев обмотки.
При вращающемся роторе.
где: x 2 S =2π f 2 L 2=2π fL 2 S = x 2 S – индуктивное сопротивление обмотки вращающегося ротора.
Для тока ротора в общем случае можно получить такое соотношение:
.
Отсюда следует, что ток ротора зависит от скольжения и возрастает при его увеличении, но медленнее, чем ЭДС.
Г) поле ротора
Обмотка ротора, как и обмотка статора, является многофазной и при появлении в ней тока создаёт своё вращающееся магнитное поле. Обозначим через n 2частоту вращения магнитного поля ротора относительно ротора.
|
|
|
n 2=(60 f 2)/ p =(60 fS)/ p.
Здесь p – число пар полюсов обмотки ротора, оно всегда равно числу пар полюсов обмотки статора.
Относительно статора магнитное поле ротора вращается с частотой
.
Из полученного соотношения следует, что магнитное поле ротора относительно статора вращается с той же частотой, что и магнитное поле статора. Таким образом, магнитные поля ротора и статора относительно друг друга неподвижны. Поэтому при анализе работы асинхронной машины можно применить те же соотношения, что и трансформаторе.
Ток статора
Так как результирующее магнитное поле асинхронной машины не зависит от её режима работы, можно составить для одной фазы уравнение магнитодвижущих сил, приравняв магнитодвижущую силу в режиме холостого хода к сумме магнитодвижущих сил в режиме нагрузки.
İ0 w 1 k 1=İ1 w 1 k 1+İ2 w 2 k 2
Отсюда İ1=İ0+İ ' 2.
Здесь I 0– ток в обмотке статора в режиме идеального холостого хода, I' 2=− I 2(w 2 k 2)/(w 1 k 1) – составляющая тока статора, которая компенсирует действие магнитодвижущей силы обмотки ротора. Полученное выражение для тока статора отражает свойство саморегулирования асинхронной машины. Чем больше ток ротора, тем больше ток статора. В режиме холостого хода ток статора минимальный. В режиме нагрузки ток статора возрастает. Ток реального холостого хода асинхронной машины I 0=(20÷60)% I 1ни значительно больше по сравнению с номинальным током, чем у трансформатора. Это объясняется тем, что величина тока I 0зависит от магнитного сопротивления среды, в которой создаётся магнитное поле. У асинхронной машины, в отличие от трансформатора, есть воздушный зазор, который создаст большое сопротивление магнитному полю.
8 Вопрос
К асинхронным машинам полностью применима формула для трансформаторной ЭДС. Пока ротор асинхронного двигателя неподвижен, его обмотка пересекается вращающимся магнитным полем с частотой n 1.
E 1= 4,44 k 1 f 1 w 1 F m; E 2= 4,44 k 2 f 1 w 2 F m,
где E 1—фазное значение ЭДС, наводимой в обмотке статора; E 2– фазное значение ЭДС, наводимой в обмотке ротора при неподвижном его состоянии (s = 1; n 2= 0); w 1, w 2—число витков в фазных обмотках статора и ротора; F m—амплитудное значение магнитного потока фазы асинхронного двигателя; k 1, k 2—обмоточные коэффициенты статора и ротора асинхронного двигателя.
|
|
|
Обмоточные коэффициенты всегда меньше единицы и в современных асинхронных машинах составляют 0,85 – 0,95. Они обусловлен тем, что в машине переменного тока витки обмотки распределены по внутренней поверхности статора и не одновременно пересекаются магнитным потоком. Поэтому ЭДС отдельных витков сдвинуты по фазе относительно друг друга и складываются не арифметически, как в трансформаторе, а геометрически (рис. 4).
Рис. 4
При неподвижном роторе частота индуцируемой в его обмотке ЭДС равна частоте сети f 1. По мере раскручивания ротора скорость (n 1– n 2) пересечения витков обмотки вращающимся магнитным полем уменьшается, а следовательно, уменьшается частота ЭДС в обмотке ротора f 2 = p (n 1– n 2)/60.
Чтобы ввести скольжение в выражение для f 2, умножим числитель и знаменатель на n 1:
f 2= p (n 1– n 2) n 1/60 n 1= (pn 1/60)[(n 1– n 2) n 1] = sf 1.
Таким образом, частота ЭДС в обмотке ротора прямо пропорциональна скольжению.
Теперь можно записать выражение для ЭДС обмотки ротора в общем случае:
E 2s= 4,44 k 2 w 2 f 2 F m= 4,44 k 2 w 2 sf 1 F m= sE 2.
Следовательно, ЭДС вращающегося ротора(E 2s) находится по ЭДС неподвижного ротора умножением его значения на скольжение, соответствующее данной частоте вращения ротора электродвигателя.
Зависимость значения величины и фазы тока от скольжения и от эдс в обмотке ротора
При работе асинхронного двигателя под действием ЭДС (E 2s), возникающей во вращающемся роторе, в цепи обмотки ротора возникнет ток I 2s, который в соответствии с законом Ома для данной цепи найдется из выражения
,
где Z 2s—полное сопротивление фазы ротора; R 2—активное сопротивление фазы ротора. Для наиболее широко распространенных двигателей R 2считают постоянным и независимым от частоты тока ротора; Х 2s— индуктивное сопротивление фазы ротора при заданном скольжении ротора s и частоте тока ротора f 2s: X 2s=w2 L 2= 2p f 2 L 2= 2p sf 1 L 2= s w1 L 2, здесь X 2 = w1 L 2совпадает с индуктивным сопротивлением обмотки неподвижного ротора. С учетом того, что E 2s= sE 2и X 2s= 2 pL 2 f 2s= sX 2, получим выражение для тока ротора в другом виде:
|
|
|
.
Из формулы видно, что ток ротора вращающегося двигателя можно определить через ЭДС неподвижного ротора. Индуктивное сопротивление X 2, входящее в выражение для тока ротора, соответствует частоте f 1 и является постоянным, а активное сопротивление электрической цепи ротора при этом зависит от скольжения и находится как отношение R 2/ s = R 2 + R 2(1– s)/ s.
Рис. 5
С учетом вышеприведенного, а также выражения для тока ротора схема замещения вращающегося ротора асинхронного электродвигателя может быть сведена к схеме замещения неподвижного ротора, представленной на рис. 5. Активное сопротивление R 2(1– s)/ s можно рассматривать как внешнее сопротивление, включенное в обмотку неподвижного ротора. В этом случае асинхронный двигатель аналогичен трансформатору, работающему на внешнюю нагрузку, величина сопротивления которого определяется скольжением, а следовательно, механической нагрузкой на валу двигателя. Так, если нагрузочный момент на валу двигателя М = 0, то скольжение s = 0. При этом R 2(1– s)/ s =¥, что соответствует работе двигателя в режиме холостого хода. Если же нагрузочный момент на валу двигателя превышает его вращающий момент, то ротор останавливается (s = 1). При этом R 2(1– s)/ s = 0, что соответствует режиму короткого замыкания асинхронного двигателя.
При построении схемы замещения асинхронного электродвигателя, параметры схемы замещения ротора, подобно тому, как это делается для вторичной обмотки трансформатора, приводят к числу витков и ЭДС обмотки статора электродвигателя. В результате полная схема замещения асинхронного двигателя имеет вид, представленный на рис. 6.
Магнитная связь обмоток статора и ротора в асинхронном двигателе на схеме замещения заменена электрической связью цепей статора и ротора. Сдвиг фаз между током и ЭДС ротора может быть определен по его схеме замещения (рис. 5).
.
При неподвижном роторе в момент запуска, когда s = 1, ток и ЭДС ротора сдвинуты по фазе на максимальный угол, 
. По мере раскручивания ротора сдвиг фаз между I 2и E 2уменьшается. При s = 0 cosj2= 1.
9 Вопрос
Схема замещения асинхронного двигателя
При практических расчетах вместо реального асинхронного двигателя, на схеме его заменяют эквивалентной схемой замещения, в которой электромагнитная связь заменена на электрическую. При этом параметры цепи ротора приводятся к параметрам цепи статора.
По сути, схема замещения асинхронного двигателя аналогична схеме замещения трансформатора. Различие в том, что у асинхронного двигателя электрическая энергия преобразуется в механическую энергию (а не в электрическую, как это происходит в трансформаторе), поэтому на схеме замещения добавляют переменное активное сопротивление r2'(1-s)/s, которое зависит от скольжения. В трансформаторе, аналогом этого сопротивления является сопротивление нагрузки Zн.
|
|
|
Величина скольжения определяет переменное сопротивление, например, при отсутствии нагрузки на валу, скольжение практически равно нулю s≈0, а значит переменное сопротивление равно бесконечности, что соответствует режиму холостого хода. И наоборот, при перегрузке двигателя, s=1, а значит сопротивление равно нулю, что соответствует режиму короткого замыкания.
Как и у трансформатора, у асинхронного двигателя есть Т-образная схема замещения.
Более удобной при практических расчетах является Г-образная схема замещения.
В Г-образной схеме, намагничивающая ветвь вынесена к входным зажимам. Таким образом, вместо трех ветвей получают две ветви, первая – намагничивающая, а вторая – рабочая. Но данное действие требует внесение дополнительного коэффициента c1, который представляет собой отношение напряжения подводимого к двигателю, к ЭДС статора.
Величина c1 приблизительно равна 1, поэтому для максимального упрощения, на практике принимают значение c1≈1. При этом следует учитывать, что значение коэффициента c1 уменьшается с увеличением мощности двигателя, поэтому более точное приближение будет соответствовать более мощному двигателю.
10 Вопрос
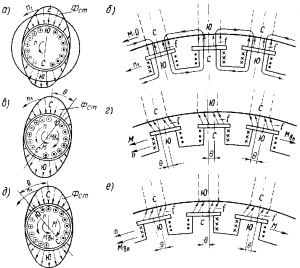Рис. 292. Электромагнитный момент в синхронной машине, образующийся в различных режимах
Электромагнитный момент. Электромагнитный момент в синхронном двигателе возникает в результате взаимодействия магнитного потока ротора (потока возбуждения Фв) с вращающимся магнитным полем, создаваемым трехфазным током, протекающим по обмотке якоря (потоком якоря Фв). При холостом ходе машины оси магнитных полей статора и ротора совпадают (рис. 292,а). Поэтому электромагнитные силы I, возникающие между «полюсами» статора и полюсами ротора, направлены радиально (рис. 292, б) и электромагнитный момент машины равен нулю. При работе машины в двигательном режиме (рис. 292, в и г) ее ротор под действием приложенного к валу внешнего нагрузочного момента Мвн смещается на некоторый угол 0 против направления вращения. В этом случае в результате электромагнитного взаимодействия между ротором и статором создаются электромагнитные силы I, направленные по направлению вращения, т. е. образуется вращающий электромагнитный момент М, который стремится преодолеть действие внешнего момента Мвн. Максимум момента Мmax
соответствует углу? = 90°, когда оси полюсов ротора расположены между осями «полюсов» статора.
Если нагрузочный момент Мвн, приложенный к валу электродвигателя, станет больше Мmax, то двигатель под действием внешнего момента Мвн останавливается; при этом по обмотке якоря неподвижного двигателя будет протекать очень большой ток. Этот режим называется выпаданием из синхронизма, он является аварийным и не должен допускаться.
При работе машины в генераторном режиме (рис. 292, д и е) ротор под действием приложенного к валу внешнего момента Мвн смещается на угол? по направлению вращения. При этом создаются электромагнитные силы, направленные против вращения, т. е. образуется тормозной электромагнитный момент М. Таким образом, при изменении значения и направления внешнего момента на валу ротора Мвн изменяется лишь угол? между осями полей статора и ротора, в то время как в асинхронной машине в этом случае изменяется частота вращения ротора.
11 Вопрос
Характеристики асинхронных двигателей. Для правильной эксплуатации асинхронного двигателя необходимо знать его характеристики: механическую и рабочие.
Механическая характеристика. Зависимость частоты вращения ротора от нагрузки (вращающегося момента на валу) называется механической характеристикой асинхронного двигателя (рис. 262, а). При номинальной нагрузке частота вращения для различных двигателей обычно составляет 98—92,5 % частоты вращения n1 (скольжение sном = 2 – 7,5 %). Чем больше нагрузка, т. е. вращающий момент, который должен развивать двигатель, тем меньше частота вращения ротора. Как показывает кривая
Рис. 262. Механические характеристики асинхронного двигателя: а — естественная; б — при включении пускового реостата
на рис. 262, а, частота вращения асинхронного двигателя лишь незначительно снижается при увеличении нагрузки в диапазоне от нуля до наибольшего ее значения. Поэтому говорят, что такой двигатель обладает жесткой механической характеристикой.
Наибольший вращающий момент Mmax двигатель развивает при некоторое скольжении skp, составляющем 10—20%. Отношение Mmax/Mном определяет перегрузочную способность двигателя, а отношение Мп/Мном — его пусковые свойства.
Двигатель может устойчиво работать только при обеспечении саморегулирования, т. е. автоматическом установлении равновесия между приложенным к валу моментом нагрузки Мвн и моментом М, развиваемым двигателем. Этому условию соответствует верхняя часть характеристики до достижения Mmax (до точки В). Если нагрузочный момент Мвн превысит момент Mmax, то двигатель теряет устойчивость и останавливается, при этом по обмоткам машины будет длительно проходить ток в 5—7 раз больше номинального, и они могут сгореть.
При включении в цепь обмоток ротора пускового реостата получаем семейство механических характеристик (рис. 262,б). Характеристика 1 при работе двигателя без пускового реостата называется естественной. Характеристики 2, 3 и 4, получаемые при подключении к обмотке ротора двигателя реостата с сопротивлениями R1п (кривая 2), R2п (кривая 3) и R3п (кривая 4), называют реостатными механическими характеристиками. При включении пускового реостата механическая характеристика становится более мягкой (более крутопадающей), так как увеличивается активное сопротивление цепи ротора R2 и возрастает sкp. При этом уменьшается пусковой ток. Пусковой момент Мп также зависит от R2. Можно так подобрать сопротивление реостата, чтобы пусковой момент Мп был равен наибольшему Мmax.
В двигателе с повышенным пусковым моментом естественная механическая характеристика приближается по своей форме к характеристике двигателя с включенным пусковым реостатом. Вращающий момент двигателя с двойной беличьей клеткой равен сумме двух моментов, создаваемых рабочей и пусковой клетками. Поэтому характеристику 1 (рис. 263) можно получить путем суммирования характеристик 2 и 3, создаваемых этими клетками. Пусковой момент Мп такого двигателя значительно больше, чем момент М’п обычного короткозамкнутого двигателя. Механическая характеристика двигателя с глубокими пазами такая же, как и у двигателя с двойной беличьей клеткой.
Рабочие характеристики. Рабочими характеристиками асинхронного двигателя называются зависимости частоты вращения n (или скольжения s), момента на валу М2, тока статора I1коэффициента полезного действия? и cos?1, от полезной мощности Р2 = Рmx при номинальных значениях напряжения U1 и частоты f1 (рис. 264). Они строятся только для зоны практической устойчивой работы двигателя, т. е. от скольжения, равного нулю, до скольжения, превышающего номинальное на 10—20%. Частота вращения n с ростом отдаваемой мощности Р2 изменяется мало, так же как и в механической характеристике; вращающий момент на валу М2 пропорционален мощности Р2, он меньше электромагнитного момента М на значение тормозящего момента Мтр, создаваемого силами трения.
Ток статора I1, возрастает с увеличением отдаваемой мощности, но при Р2 = 0 имеется некоторый ток холостого хода I0. К. п. д. изменяется примерно так же, как и в трансформаторе, сохраняя достаточно большое значение в сравнительно широком диапазоне нагрузки.
Наибольшее значение к. п. д. для асинхронных двигателей средней и большой мощности составляет 0,75—0,95 (машины большой мощности имеют соответственно больший к. п. д.). Коэффициент мощности cos?1 асинхронных двигателей средней и большой мощности при полной нагрузке равен 0,7—0,9. Следовательно, они загружают электрические станции и сети значительными реактивными токами (от 70 до 40% номинального тока), что является существенным недостатком этих двигателей.
Рис. 263. Механическая характеристика асинхронного двигателя с повышенным пусковым моментом (с двойной беличьей клеткой)
Рис. 264. Рабочие характеристики асинхронного двигателя
При нагрузках 25—50 % номинальной, которые часто встречаются при эксплуатации различных механизмов, коэффициент мощности уменьшается до неудовлетворительных с энергетической точки зрения значений (0,5—0,75).
При снятии нагрузки с двигателя коэффициент мощности уменьшается до значений 0,25—0,3, поэтому нельзя допускать работу асинхронных двигателей при холостом ходе и значительных недогрузках.
Вопрос
Работа при пониженном напряжении и обрыве одной из фаз.
Понижение напряжения сети не оказывает существенного влияния на частоту вращения ротора асинхронного двигателя. Однако в этом случае сильно уменьшается наибольший вращающий момент, который может развить асинхронный двигатель (при понижении напряжения на 30% он уменьшается примерно в 2 раза). Поэтому при значительном падении напряжения двигатель может остановиться, а при низком напряжении — не включиться в работу.
На э. п. с. переменного тока при уменьшении напряжения в контактной сети соответственно уменьшается и напряжение в трехфазной сети, от которой питаются асинхронные двигатели, приводящие во вращение вспомогательные машины (вентиляторы, компрессоры, насосы). Для того чтобы обеспечить нормальную работу асинхронных двигателей при пониженном напряжении (они должны нормально работать при уменьшении напряжения до 0,75Uном), мощность всех двигателей вспомогательных машин на э. п. с. берется примерно в 1,5—1,6 раза большей, чем это необходимо для привода их при номинальном напряжении. Такой запас по мощности необходим также из-за некоторой несимметрии фазных напряжений, так как на э. п. с. асинхронные двигатели питаются не от трехфазного генератора, а от расщепителя фаз. При несимметрии напряжений фазные токи двигателя будут неодинаковы и сдвиг между ними по фазе не будет равен 120°. В результате по одной из фаз будет протекать больший ток, вызывающий увеличенный нагрев обмоток данной фазы. Это заставляет ограничивать нагрузку двигателя по сравнению с работой его при симметричном напряжении. Кроме того, при несимметрии напряжений возникает не круговое, а эллиптическое вращающееся магнитное поле и несколько изменяется форма механической характеристики двигателя. При этом уменьшаются его наибольший и пусковой моменты. Несимметрию напряжений характеризуют коэффициентом несимметрии, который равен среднему относительному (в процентах) отклонению напряжений в отдельных фазах от среднего (симметричного) напряжения. Систему трехфазных напряжений принято считать практически симметричной, если этот коэффициент меньше 5 %.
При обрыве одной из фаз двигатель продолжает работать, но по неповрежденным фазам будут протекать повышенные токи, вызывающие увеличенный нагрев обмоток; такой режим не должен допускаться. Пуск двигателя с оборванной фазой невозможен, так как при этом не создается вращающееся магнитное поле, вследствие чего ротор двигателя не будет вращаться.
Использование асинхронных двигателей для привода вспомогательных машин э. п. с. обеспечивает значительные преимущества по сравнению с двигателями постоянного тока. При уменьшении напряжения в контактной сети частота вращения асинхронных двигателей, а следовательно, и подача компрессоров, вентиляторов, насосов практически не изменяются. В двигателях же постоянного тока частота вращения пропорциональна питающему напряжению, поэтому подача этих машин существенно уменьшается.
13 Вопрос.
Пусковые свойства двигателей.
При пуске ротор двигателя, преодолевая момент нагрузки и момент инерции, разгоняется от частоты вращения п = 0 до п. Скольжение при этом меняется от s п = 1 до s. При пуске должны выполняться два основных требования: вращающий момент должен бить больше момента сопротивления (М вр> М с) и пусковой ток I п должен быть по возможности небольшим.
В зависимости от конструкции ротора (короткозамкнутый или фазный), мощности двигателя, характера нагрузки возможны различные способы пуска: прямой пуск, пуск с использованием дополнительных сопротивлений, пуск при пониженном напряжении и др. Ниже различные способы пуска рассматриваются более подробно.
Прямой пуск. Пуск двигателя непосредственным включением на напряжение сети обмотки статора называется прямым пуском. Схема прямого пуска приведена на рис. 3.22. При включении рубильника в первый момент скольжение s = l, а приведенный ток в роторе и равный ему ток статора
, (3.37)
максимальны (см.п.3.19 при s=1). По мере разгона ротора скольжение уменьшается и поэтому в конце пуска ток значительно меньше, чем в первый момент. В серийных двигателях при прямом пуске кратность пускового тока kI = IП / I1НОМ = (5,…,7), причем большее значение относится к двигателям большей мощности.
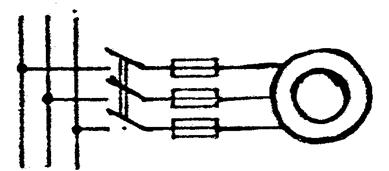
Рис. 3.22
Значение пускового момента находится из (3.23) при s = 1:
. (3.38)
Из рис. 3.18 видно, что пусковой момент близок к номинальному и значительно меньше критического. Для серийных двигателей кратность пускового момента МП/ МНОМ = (1.0,…,1.8).
Приведенные данные показывают, что при прямом пуске в сети, питающей двигатель, возникает бросок тока, который может вызвать настолько значительное падение напряжение, что другие двигатели, питающиеся от этой сети, могут остановиться. С другой стороны, из-за небольшого пускового момента при пуске под нагрузкой двигатель может не преодолеть момент сопротивления на валу и не тронется с места. В силу указанных недостатков прямой пуск можно применять только у двигателей малой и средней мощности (примерно до 50 кВт).
Пуск двигателей с улучшенными пусковыми свойствами. Улучшение пусковых свойств асинхронных двигателей достигается использованием эффекта вытеснения тока в роторе за счет специальной конструкции беличьей клетки. Эффект вытеснения тока состоит в следующем: потокосцепление и индуктивное сопротивление X2 проводников в пазу ротора тем выше, чем ближе ко дну паза они расположены (рис.3.23). Также X2 прямо пропорционально частоте тока ротора.
Следовательно, при пуске двигателя, когда s=1 и f2 = f1 = 50 Гц, индуктивное сопротивление X2 = max и под влиянием этого ток вытесняется в наружный слой паза. Плотность тока j по координате h распределяется по кривой, показанной на рис.3.24. В результате ток в основном проходит по наружному сечению проводника, т.е. по значительно меньшему сечению стержня, и, следовательно, активное сопротивление обмотки ротора R2 намного больше, чем при нормальной работе. За счет этого уменьшается пусковой ток и увеличивается пусковой момент МП (см. (3.37), (3.38)). По мере разгона двигателя скольжение и частота тока ротора падает и к концу пуска достигает 1 – 4 Гц. При такой частоте индуктивное сопротивление мало и ток распределяется равномерно по всему сечению проводника. При сильно выраженном эффекте вытеснения тока становится возможным прямой пуск при меньших бросках тока и больших пусковых моментах.
К двигателям с улучшенными пусковыми свойствами относятся двигатели, имеющие роторы с глубоким пазом, с двойной беличьей клеткой и некоторые другие.
Рис.3.23 Рис. 3.24
Двигатели с глубокими пазами. Как показано на рис.3.25, паз ротора выполнен в виде узкой щели, глубина которой примерно в 10 раз больше, чем ее ширина. В эти пазы-щели укладывается обмотка в виде узких медных полос. Распределение магнитного потока показывает, что индуктивность и индуктивное сопротивление в нижней части проводника значительно больше, чем в верхней части. Поэтому при пуске ток вытесняется в верхнюю часть стержня и активное сопротивление значительно увеличивается. По мере разгона двигателя скольжение уменьшается, и плотность тока по сечению становится почти одинаковой. В целях увеличения эффекта вытеснения тока глубокие пазы выполняются не только в виде щели, но и трапецеидальной формы. В этом случае глубина паза несколько меньше, чем при прямоугольной форме.
Рис.3.25
Рис.3.26
Двигатели с двойной клеткой. В таких двигателях обмотки ротора выполняются в виде двух клеток (рис.3.26): во внешних пазах 1 размещается обмотка из латунных проводников, во внутренних 2 – обмотка из медных проводников. Таким образом, внешняя обмотка имеет большее активное сопротивление, чем внутренняя. При пуске внешняя обмотка сцепляется с очень слабым магнитным потоком, а внутренняя – сравнительно сильным полем. В результате ток вытесняется во внешнюю клетку, а во внутренней тока почти нет.
По мере разгона двигателя ток из внешней клетки переходит во внутреннюю и при s =sНОМ протекает в основном по внутренней клетке. Ток во внешней клетке при этом сравнительно небольшой. Результирующий пусковой момент, складывающийся из моментов от двух клеток, значительно больше, чем у двигателей нормальной конструкции, и несколько больше, чем у двигателей с глубоким пазом. Однако следует иметь в виду, что стоимость двигателей с двойной клеткой ротора выше.
|
|
|
