 |
Основные характеристики кристаллических структур
|
|
|
|
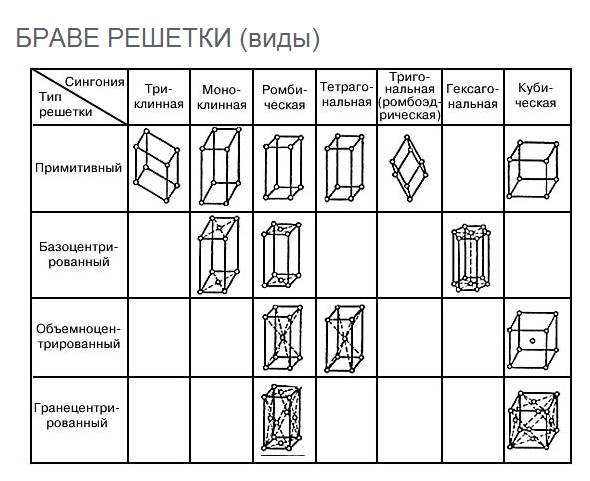
БРАВЕ РЕШЕТКИ

Схема построения
БРАВЕ́ РЕШЕТКИ, 14 трехмерных геометрических решеток, характеризующих все возможные типы трансляционной симметрии кристаллов. Браве решетки образуются действием операции переноса (трансляции) на любую точку кристалла.
О. Браве в 1848 показал, что все многообразие кристаллических структур можно описать с помощью 14 типов решеток, отличающихся формами элементарных ячеек и симметрией и подразделяющихся на 7 кристаллографических сингоний. Эти решетки были названы решетками Браве.
Решетки Браве различаются симметрией элементарной ячейки, т. е. соотношением между ее ребрами и углами, а также центрированностью.
Для выбора ячейки Браве используют три условия:
- симметрия элементарной ячейки должна соответствовать симметрии кристалла, точнее наиболее высокой симметрии той сингонии, к которой относится кристалл. Ребра элементарной ячейки должны быть трансляциями решетки;
- элементарная ячейка должна содержать максимально возможное число прямых углов или равных углов и равных ребер;
- элементарная ячейка должна иметь минимальный объем.
По характеру взаимного расположения основных трансляций или расположению узлов все кристаллические решетки разбиваются на четыре типа: примитивные (Р), базоцентрированные (С), объемно-центрированные (I), гранецентрированные (F).
В примитивной Р -ячейке узлы решетки располагаются только по вершинам ячейки, в объемно-центрированной I -ячейке — один узел в центре ячейки, в гранецентрированной F -ячейке — по одному узлу в центре каждой грани, в базоцентрированной С -ячейке — по одному узлу в центрах пары параллельных граней.
Совокупность координат узлов, входящих в элементарную ячейку, называется базисом ячейки. Всю кристаллическую структуру можно получить, повторяя узлы базиса совокупностью трансляций ячейки Браве.
|
|
|
Для некоторых сингоний элементарная ячейка может содержать узлы не только в углах, но и в центре ячейки, всех или некоторых граней. При этом возможен трансляционный перенос не только на периоды элементарной ячейки, но и на половины диагоналей граней ячейки или пространственных диагоналей. Кроме обязательной трансляционной инвариантности, решетка может переходить в себя при других преобразованиях, к которым относятся повороты, отражения и инверсии. Именно эти дополнительные симметрии определяют тип решетки Браве и отличают ее от других.
Типы решеток Браве:
- кубические: примитивная, объемно-центрированная и гранецентрированная;
- гексагональная, тригональная;
- тетрагональные: примитивная и объемно-централизованная;
- ромбические: примитивная, базо-, объемно- и гранецентрированные;
- моноклинные: примитивная и базоцентрированная;
- триклинная.
Сингони́я (от греч. σύν, «согласно, вместе, рядом», и γωνία, «угол» — дословно «сходноугольность») — классификация кристаллографических групп симметрии, кристаллов и кристаллических решёток в зависимости от системы координат (координатного репера). Группы симметрии с единой координатной системой объединяются в одну сингонию.
Кристаллы, принадлежащие к одной и той же сингонии, имеют подобные углы и рёбра элементарных ячеек.
· Низшая категория (все трансляции не равны друг другу)
· Триклинная: {\displaystyle a\neq b\neq c}, {\displaystyle \alpha \neq \beta \neq \gamma \neq 90^{\circ }}
· Моноклинная: {\displaystyle a\neq b\neq c}, {\displaystyle \alpha =\gamma =90^{\circ },\beta \neq 90^{\circ }}
· Ромбическая: {\displaystyle a\neq b\neq c}, {\displaystyle \alpha =\beta =\gamma =90^{\circ }}
· Средняя категория (две трансляции из трёх равны между собой)
· Тетрагональная: {\displaystyle a=b\neq c}, {\displaystyle \alpha =\beta =\gamma =90^{\circ }}
|
|
|
· Гексагональная: {\displaystyle a=b\neq c}, {\displaystyle \alpha =\beta =90^{\circ },\gamma =120^{\circ }}
· Высшая категория (все трансляции равны между собой)
· Кубическая: {\displaystyle a=b=c}, {\displaystyle \alpha =\beta =\gamma =90^{\circ }}

Основные характеристики кристаллических структур
Кристаллические мат-лы характ наличием дальнего порядка, кот характ. тем, что в нем можно выделить некий объем, расположение атома в котором повторяется но всему объему.
В аморфных мат-ах имеет место ближний порядок, кот. характ. тем. что нет повторения объемов.
Крист. структуру удобно описывать с помощью З х мерной сетки прямых липни, которые делят прос-во на параллелепипиды равных размеров. Пересеч линий образ 3х мерную пространств. решетку. Узлы решетки, как правило, соответствуют расположению атомов в кристалле. Атом колеблется
около этих положений. Если в такой пространственной решетке можно выделить некий объем, перемещением которого в 3х направ. позволяет выстроив весь кристалл, то гов. Что найдена элемент, ячейка.
Элемент ячейку принято характеризовать 6 параметрами: а, Ь, с - длина ребер параллелепипеда, α, β, γ.
Форма элемент ячейки определяет кристаллографическую систему координат - сингония. В качестве осей выбирают направления ребер -элем, ячейки, а сами ребра являются единицами измерения. Число прямых углов и равных сторон должно быть mах,а объем элем ячейки должен быть min.
|
|
|


