 |
Активизация творческой деятельности учащихся на уроках математики
|
|
|
|
"Основная задача обучения математике - обеспечить прочное и созидательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования" - говорится в объяснительной записке программы по математике.
Проблема развития ученика является одной из сложнейших задач в педагогической практике. Решение этой проблемы зависит от того, на получение какого именно результата ориентируется учитель в своей работе. Критерием деятельности является конечный результат: либо дать ученику лишь набор по предмету, либо сформировать личность, готовую к творческой деятельности.
Наша школа ставит своей целью развитие всесторонне развитой личности и конечно конечный результат деятельности учителя - новообразования в личности учащегося. К.Д.Ушинский писал: "Сделать учебную работу насколько возможно интересной для ребенка и не превратить эту работу в забаву - одна из труднейших и важнейших задач дидактики".
Развитие учащихся зависит от той деятельности, которую они выполняют в процессе обучения - репродуктивную или продуктивную (творческую).
Возможности школьников различны, но они должны приводить в движение для развития творческой деятельности школьника. Имеются разные методы: исследовательский, поисковый, метод проблемной ситуации, логико-содержательное построение курса. Важно лишь пробудить мыслительный процесс ученика.
Одним из активных методов на уроке является создание проблемных ситуаций, который на много улучшает усвоение материала учениками и развивает в них внимательность, гибкость ума, следствием чего является высокая активность учащихся на уроках. Нельзя заставить ребенка слепо штудировать предмет в погоне за всеобщей успеваемостью. Необходимо давать возможность ученику экспериментировать и не бояться ошибок, воспитывать у учащихся смелость быть не согласным с учителем.
|
|
|
Предмет должен преподаваться в атмосфере дружелюбия, увлеченности, естественной реакции большинства учеников.
Для меня в процессе обучения главным является постановка перед учащимися на уроках какой-то маленькой проблемы и старание совместно с ними ответить на поставленный вопрос.
Как же создавать эти проблемные ситуации, какие есть варианты их постановки.
Пример №1:
В понимании детей учитель - это компьютер, который не может ошибиться никогда, и они обычно слепо копируют его решение.
Решаю быстро уравнение:
(3Х + 7) х 2 - 3 = 17
Х + 14 - 3 = 17
Х = 17 - 14 - 3 (умышленная ошибка)
Х = 0
Х = 0
Естественно при проверке ответ не сходится. Ищут ошибку. Дети решают проблему. После этого учащиеся очень внимательно следят за мыслью и решением учителя. Результат - внимательность и заинтересованность на уроке.
Пример №2. Даю задачу на дом и говорю: "У меня не получается". Попробуйте вы, обращайтесь к кому хотите за помощью. Хотя задача решается. На другой урок у них радостные лица - они решили.
Пример №3. Решаю квадратное уравнение.
3Х2 - 2Х - 2 = 0
Д = (-2)2 - 4 х 3 х (-2) = 25
(Ошибка, заставляю делать проверку. Не получается. Где ошибка? Находят Д = 28)
Вот такие примеры активизируют деятельность учащихся.
Задача учителя - привить своим ученикам привычку к упорному, самостоятельному, творческому труду, выработать у учащихся умение преодолевать трудности при решении задач, а также при любой работе, связанной с учебной деятельностью.
Одним из мощных рычагов воспитания трудолюбия, желания и умения хорошо учиться является создание условий, обеспечивающих ребенку успех в учебной программе, на пути от незнания к знанию, от неумения к умению. К таким условиям, безусловно, можно отнести процесс решения нестандартных, логических задач, задач - головоломок, на соображение и догадку.
|
|
|
Задача будит мысль учащегося, активизирует его мыслительную деятельность. Решение задач считается гимнастикой ума.
Готовясь к уроку, я подбираю материал к нему и формы работы, чтобы обеспечить мыслительную деятельность каждого ученика каждую минуту.
Что же нужно знать тому, кто стремится создать на своих уроках положительную эмоциональную обстановку? Прежде всего, то, что на уроках такой строгой науки, как математика, сделать это можно только введением в них занимательных моментов.
Занимательные моменты могут быть связаны с изучаемой темой, а могут быть с нею не связанными.
Пример №1: Тема: "Сложение и вычитание десятичных дробей" (5 кл.). Дети слегка притомились, выполняя однотипные упражнения. Я говорю: "Вижу, что 18 из вас уже научились складывать дроби, а 16 хорошо вычитаются. А вы теперь сообразите, сколько у нас в классе ребят, которые научились уже и складывать и вычитать дроби, если всего на уроке сегодня 21 человек?"
Это элемент занимательности не имеет никакого отношения к теме урока.
Пример №2: Урок в 7 классе по теме: "Решение линейных уравнений". Предлагаю задачу: На зимних каникулах из 36 учащихся класса только двое просидели дома, а 25 ребят ходили в кино, 15 - в театр, 17 - в цирк. Кино и театр посетили 11 человек, кино и цирк - 10, театр и цирк - 4. сколько ребят побывало и в кино, и в театре, и цирке?
Решается линейное уравнение: 25 + (3 + Х) + (4 - Х) + Х = 34
Это занимательный элемент напрямую связан с темой урока. Занимательные задачи отличаются по форме и по содержанию.
Рассмотренные выше задачи с элементами занимательности по содержанию. А можно взять задание из школьного учебника и подать его как игру.
Обычная форма задания:
функция задана формулой У = Х + 5
найдите значение функции при Х = 0, 7, -5, 1.
Занимательная форма задания: Приглашаю к доске ученика, даю ему карточку, на которой написано У = Х + 5. На доске заготовлена таблица:
| Х | |||||||
| У |
|
|
|
Ученик из класса называет какое-нибудь значение Х. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение У. Затем другой ученик из класса называет другое значение Х и ученик у доски проделывает те же операции. Задача класса - "угадать" формулу, записанную на карточке. Выигрывает тот ученик, который первый назовет формулу.
Главный фактор занимательности - это приобщение учащихся к творческому поиску, активизация их самостоятельной исследовательской деятельности, так как уникальность занимательной задачи служит мотивом к учебной деятельности, развивая и тренируя мышление вообще и творческое, в частности.
Следующий момент занимательности - это смекалка. Смекалка - это особый вид проявления творчества. Она выражается в результате анализа сравнений, обобщений, установления связей, аналогии, выводов, умозаключений. Эти качества можно и нужно развивать в процессе обучения.
В своей практике я использую такие занимательные элементы урока:
. Петух на одной ноге весит 4 кг. А на двух?
. Половина - треть числа. Какое это число?
. В семье 5 сыновей и у каждого есть сестра. Сколько детей в семье?
. Кирпич весит 1,5 кг и ещё полкирпича. Какова масса кирпича?
А также задачи на внимание и сравнение.
. Определите, сколько треугольников вы видите на рис.1 и квадратов на рис.2а,б?

6. Сколько треугольников на каждом рисунка?
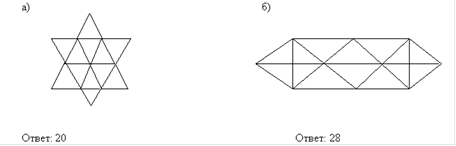
7. Подсчитать количество отрезков.

8. Определите, что общего в данных фигурах, а в чём различие?

9. Уберите лишнюю фигуру. Ответ обоснуйте.

Большой интерес у ребят вызывает решение старинных задач. Таких как:
.
На две партии разбившись,
Забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась.
Криком радостным двенадцать
Воздух свежий оглашали.
Вместе сколько, ты подскажешь,
Обезьян там было в роще?
Ответ: 16 или 48.
.
Хозяин нанял работника с таким условием: за каждый рабочий день будет платить ему 20 копеек, а за каждый нерабочий день - вычитать 30 копеек. По прошествии 60 дней работник ничего не заработал. Сколько было рабочих дней?
|
|
|
Ответ: 36 дней.
В решении таких задач используется уравнение. Ничто так не способствует формированию мыслительной культуры и ничего так не оживляет урок, как решение логических задач.
Учу детей решать логические задачи с помощью таблицы. Привожу несколько примеров:
задача: "Спортивные соревнования". Коля, Боря, Вова, Юра заняли первые четыре места в спортивном соревновании. На вопрос, какие места они заняли, они четко ответили:
Коля не занял ни первое, ни четвертое место;
Боря занял второе место;
Вова не был последним.
Какое место занял каждый мальчик?
Решение:
| Мальчики | Призовые места | |||
| I | II | III | IV | |
| Коля | 0 | 0 | 1 | 0 |
| Боря | 0 | 1 | 0 | 0 |
| Вова | 1 | 0 | 0 | 0 |
| Юра | 0 | 0 | 0 | 1 |
Ответ: Володя занял I место, Боря - II место, Коля - III место, Юра - IV место.
задача: "На конкурсе". Однажды на конкурсе за круглым столом оказалось пятеро ребят родом из Москвы, Санкт-Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алёша, Коля и Витя.
Известно, что:
. Петербуржец сидел между Юрой и Толей, а напротив него сидели пермяк и Алёша;
. Коля никогда не был в Санкт-Петербурге;
. Юра не был в Москве и Томске;
. Томич с Толей регулярно переписываются.
Определите, в каком городе живет каждый из ребят.
Решение:
| Город | Имя | ||||
| Юра | Толя | Алеша | Коля | Витя | |
| Москва | - | + | - | - | - |
| Санкт-Петербург | - | - | - | - | + |
| Новгород | + | - | - | - | - |
| Пермь | - | - | - | + | - |
| Томск | - | - | + | - | - |
Ответ: Юра живет в Новгороде, Толя - в Москве, Алеша - в Томске, Коля - в Перми, Витя - в Санкт-Петербурге.
Эти задачи носят занимательный характер и не требуют большого запаса математических знаний, поэтому они привлекают даже тех учащихся, которые не очень любят математику.
Одним из путей активизации творческой деятельности учащихся является решение нестандартных задач. Эти задачи в основном встречаются на олимпиадах. Во внеурочное время с учащимися решаем такие задачи:
Пример: Числа написаны подряд: 1,2,3,4,5…., 2000. первое, третье, пятое и т.д. по порядку вычеркивают. Из оставшихся 1000 чисел снова вычеркивают первое, третье, пятое и т.д., повторяя пока не останется одно число. Что это за число?
Решение: Выписываем ряды:
) 1,2,3,4,5,6,7,….. 2000 (2000 чисел)
) 2,4,6,8,10…..2000 (1000 чисел, 2n - формула чисел)
) 4,8,12,16,20…..2000 (500 чисел, 4n - формула чисел)… и так далее 10 строк.
Ученики увидели, что остаются степени числа 2.
Значит, останется число 24 < 2000, а это 210 = 1024, т.к. 211 = 2048 > 2000.
Ответ: 1024.
Творческая деятельность учащихся не ограничивается лишь приобретением нового. Работа будет творческой, когда в ней проявляется собственный замысел учащихся, ставятся новые задачи и самостоятельно решаются при помощи приобретаемых знаний.
|
|
|
Решение интересных, занимательных задач создает атмосферу взаимодействия, и я радуюсь повышению математической культуры своих учеников и своей профессиональной компетентности.
ЗАКЛЮЧЕНИЕ
Творчество - одно из сложных и таинственных явлений человеческой жизни. Творчество- это деятельность, порождающая нечто качественно новое и отличающаяся неповторимостью, оригинальностью и общественно-исторической уникальностью.
Разделение педагогической деятельности на творческую и нетворческую - абсолютно условное. Нельзя утверждать, что один опыт - абсолютно творческий, а другой - абсолютно не творческий. Т.к. творчество - это новизна, то в учебном процессе она представлена, прежде всего, научными открытиями, выявлением ранее не опознанных закономерностей обучения и воспитания, исследовательской, экспериментальной разработкой высокоэффективных методик, позволяющих решать задачи, как современной школы, так и школы будущего. Но не только.
На этом же уровне находится и новаторство в практике, под которым мы подразумеваем создание принципиально новых дидактических или воспитательных целостных разработок, позволяющих существенно повысить эффективность педагогического процесса. Новаторство, как правило, связано с нестандартными подходами, нешаблонными решениями наиболее сложных и актуальных педагогических проблем.
Творчество так же может проявляться в использовании кем-то созданного опыта в новых условиях, совершенствовании, рационализации, модернизации известного в соответствии с новыми задачами, в освоении научных разработок и их развитии, в импровизации.
Объектом и итогом педагогического творчества является создание личности, ее творение. Истинный педагогический труд не может быть не творческим, т.к. нет одинаковых учеников, учителей, обстоятельств. Современное творчество - активный процесс. Раченко выделяет 4 уровня творчества: профессиональное становление, стихийное самосовершенствование, планомерная рационализация и, наконец, уровень оптимизации процесса и результатов труда.
Современного творческого учителя отличает прежде всего высокий уровень идейно-нравственного сознания, являющийся надежной гарантией активизации его творческих усилий. Ему характерны такие качества: объективность, активность, разносторонность, целеустремленность, интегративность, комплексность, динамизм, гибкость, мобильность, аналитичность, самокритичность и критичность.
Как показывает жизнь, успех сопутствует в работе только тем учителям, у кого и общечеловеческие качества, и профессиональные, и общая культура личности (разносторонние интересы, развитый интеллект, широкий кругозор, эрудиция) высоко развиты. Постоянное развитие общей культуры личности- категорическое требование, предъявляемое к любому учителю, и особенно творческому, т.к. она является фундаментом, на котором строится любая педагогическая деятельность.
Творческая лаборатория учителя - это условное название его деятельности по самообразованию, творческому конструированию уроков и мероприятий, поиск и использование источников, питающих творческий потенциал.
Под оптимизацией мы понимаем выбор системы мер, которая поможет учителю получать наивысшие для конкретных условий результаты деятельности при минимальных необходимых затратах времени. Где бы не осуществлялась оптимизация, при планировании урока или в его процессе, она неизбежно приводит к творчеству, т.к. выбор, реализация различных методик - это творческая деятельность.
Оптимизация очень часто используется в педагогической деятельности, что стимулирует к творчеству как учителя, так и ученика. Нет ни одного ребенка, которого природа не наделила бы скрытым творческим потенциалом. Творческий учитель должен выявить его. Такой учитель должен, прежде всего быть нацеленным на формирование творческой личности школьника, обладать педагогическим тактом, способностью к эмпатии, уметь развивать детское воображение, артистизм, уметь ставить интересные, занимательные вопросы, создавать интересные ситуации, обладать чувством юмора.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
. Богоявленская Д.Б. Пути к творчеству. - М.: Знание, 1981.
. Вербова К.В., Кондратьева С.В. Психология труда и личности учителя. - Гродно, 1991.
. Гусев Ю.А. Познание и творчество. - Минск: Университетское,1987.
. Кудрявцев В.Т., Уразалиева Т.К. О творческой природе человеческой деятельности // проблема психологии творчества в работе с людьми: Тез. докл. и выст. на Всесоюзной научной конференции. - Гродно, 1990. - Ч.1.
. Кулюткин Ю.Н. Творческое мышление профессиональной деятельности // Вопр. психологии. - 1986. - №2
. Ломов Б.Ф. Методологические и теоретические проблемы психологии.- М.: Наука
. Макаренко А.С. Педагогические сочинения: В8т. - М.: Педагогика, 1983. - Т.3. Педагогическая поэма.
. Матюшкин А.М. Проблемные ситуации в мышлении и обучении. - М., Педагогика. - 1978.
. Моделирование педагогических ситуаций / Под ред. Ю.Н. Кулюткина, Г.С. Сухобской. - И.: Педагогика, 1981.
. Пономарев Я.А. Психология творчества. - М.: Наука, 1976.
. Харин Ю.А., Мамыкин И.Л. Сущность творческой деятельности // Творчество в научном познании / Под ред. Д.И. Широканова. - Минск,1976.
. Шацкий С.Т. Избранные педагог. Сочинения: В2т. - М., Педагогика, 1980. - Т.2.
. Творчество //БСЭ. - М., 1976. - Т.25.
. Васильева Ю.С. и др. Опыт разработки модели внедрения современных методик обучения иностранным языкам//Методист №4.2009 г.
. Молокостова Л.А. Реализация инновационных образовательных программ как условие развития школы//Методист №2.2009 г.
. Гаврилова Т.Д. Занимательная математика. Изд. "Учитель".
. Фарков А.В. Математические олимпиады. Гуманитарный издательский центр "Владос", 2004г.
. Перельман Я.И. Живая математика. М., Наука, 1967г.
. Математика. Учебно-методическая газета №41/2000, №7/2005.
. Богомолова О.Б. Логические задачи. М., 2005.
|
|
|


