 |
Общие указания по выполнению и оформлению контрольных работ
|
|
|
|
В соответствии с учебным планом и рабочей программой по дисциплине Математика каждый студент дистанционной формы обучения должен выполнить контрольную работу.
Контрольные работы выполняются по индивидуальным вариантам, выдаваемым каждому студенту преподавателями. Студент выбирает номер варианта, соответствующий номеру последней цифры в зачетной книжке. Сроки сдачи контрольных работ на проверку указаны в индивидуальном графике студента. Однако эти сроки являются крайними. Чтобы работа была своевременно прорецензирована, при необходимости доработана и сдана повторно, ее надлежит представить значительно раньше указанного срока.
Если в ходе написания работы у студента появляются вопросы или затруднения в решении задач контрольной работы, он может обратиться за письменной консультацией к преподавателю, используя, например, электронную почту.
При выполнении контрольных работ необходимо соблюдать следующие правила:
1) работа должна быть выполнена в текстовом редакторе MS Word;
2) перед решением каждой задачи нужно привести полностью ее условие;
3) следует придерживаться той последовательности при решении, в какой они даны в задании, строго сохраняя при этом нумерацию заданий;
4) не допускается замена задач контрольной работы другими;
5) решение задач должно сопровождаться пояснениями; нужно привести в общем виде используемые формулы с объяснением употребляемых обозначений;
6) на титульном листе контрольной работы должно быть ясно написаны фамилия, имя, отчество (полностью) студента, специальность, курс, вариант.
Если работа получила в целом положительную оценку (зачет), но в ней есть отдельные недочеты, то нужно сделать соответствующие исправления и дополнения и отправить их преподавателю. Если работа не зачтена, ее необходимо полностью переделать
|
|
|
Контрольная работа не засчитывается, если ее вариант не соответствует выданному студенту.
Студент, не получивший зачет по контрольной работе, к экзамену или зачету не допускается.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1
Задание 1: Даны множества A={1,2,7,8,9} и B={2,3,7,8,10}
Найти: A∩B, AÈB, A\B, AΔB
Задание 2. Дана матрица А. Построить соответствующий ей орграф, имеющий матрицу А своей матрицей смежности. Найти матрицу инцидентности для построенного орграфа. 
Задание 3. Вычислить неопределенные интегралы
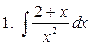


Задание 4. Вычислить площадь фигуры, ограниченной линиями:

Задание 5. Найти общее решение дифференциального уравнения 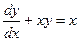
Задание 6. В группе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,1 возможного значения х1, математическое ожидание M(x) = 3,9 и дисперсия D(x) = 0,09.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =2+3i z2 = 7-2i
Задание 9. Вычислить пределы функций
1. 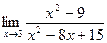 2.
2. 
Вариант 2
Задание 1. Найдите А ∩ В, если
а) А = (–2; 6), В = (1; 7);
б) А = [0; 4], B = [4; 8];
в) А = (–∞; +∞), В = (–3; 9);
Задание 2. Дана матрица А. Построить соответствующий ей орграф, имеющий матрицу А своей матрицей смежности. Найти матрицу инцидентности для построенного орграфа. 
Задание 3. Вычислить неопределенные интегралы



Задание 4. Вычислить площадь фигуры ограниченной линиями:
|
|
|
1.  , y=0, x=2, x=-1
, y=0, x=2, x=-1
Задание 5. Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным решениям  при x=2:
при x=2:
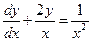
Задание 6. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только
один раз?
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,3 возможного значения х1, математическое ожидание M(x) = 3,7 и дисперсия D(x) = 0,21.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =2-3i z2 = 7+2i
Задание 9. Вычислить пределы функций
1.  2.
2. 
Вариант 3
Задание 1. Пусть заданы множества А, В и С такие, что А ∩ В = {2; 3},
А È В = {1; 2; 3; 5; 7; 8}, А ∩ C = {1}, C È В = {1; 2; 3; 5; 6; 7; 8}.
Найдите множества A, B и С.
Задание 2. Дана матрица А. Построить соответствующий ей орграф, имеющий матрицу А своей матрицей смежности. Найти матрицу инцидентности для построенного орграфа. 
Задание 3. Вычислить неопределенные интегралы
1. 


Задание 4. Вычислить площадь фигуры ограниченной линиями:
1.  , y=0
, y=0
Задание 5. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
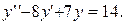
Задание 6. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр.
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,5 возможного значения х1, математическое ожидание M(x) = 3,5 и дисперсия D(x) = 0,25.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =3+5i z2 = 7-2i
Задание 9. Вычислить пределы функций
1. 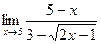 2.
2. 
Вариант 4
Задание 1. Найдите А ∪ В и А ∩ В, если А = {x | x4-13x2+36=0},
В = {x | x4 -8x2 +9=0 };
Задание 2. Задать граф с помощью матриц смежности и инцидентности.

Задание 3. Вычислить неопределенные интегралы
1. 
 3.
3.  ;
;
Задание 4. Вычислить площадь фигуры ограниченной линиями:
|
|
|
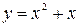 ,
, 
Задание 5. Решить линейное дифференциальное уравнение с постоянными коэффициентами:

Задача 6. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,7 возможного значения х1, математическое ожидание M(x) = 3,3 и дисперсия D(x) = 0,21.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =2-3i z2 = 1+4i
Задание 9. Вычислить пределы функций
1.  2.
2. 
Вариант 5
Задание 1. Найдите А ∪ В и А ∩ В, если А = {x | 3x – 9 < 0}, В = {x | 2x + 6 > 0}.
Задание 2. Дана матрица А. Построить соответствующий ей орграф, имеющий матрицу А своей матрицей смежности. Найти матрицу инцидентности для построенного орграфа. 
Задание 3. Вычислить неопределенные интегралы

 3.
3. 
Задание 4. Вычислить площадь фигуры ограниченной линиями:
 ,
, 
Задание 5. Решить дифференциальное уравнение первого порядка:
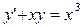
Задача 6. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать.
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,9 возможного значения х1, математическое ожидание M(x) = 3,1 и дисперсия D(x) = 0,09.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =2-3i z2 = 1-4i
Задание 9. Вычислить пределы функций
1.  2.
2. 
Вариант 6
Задание 1. Найдите A \ B, В \ А, (A \ B) È (В \ А):
а) А = [–11; 4], B = (2; 8];
б) A = [2; 7]; B = [8; 12];
в) A = (–∞; 5]; B = (1; +∞).
|
|
|
Задание 2. Дана матрица А. Построить соответствующий ей орграф, имеющий матрицу А своей матрицей смежности. Найти матрицу инцидентности для построенного орграфа. 
Задание 3. Вычислить неопределенные интегралы
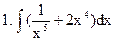 2.
2. 

Задание 4. Вычислить площадь фигуры ограниченной линиями:
 ,
, 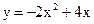
Задание 5. Решить линейное дифференциальное уравнение первого порядка
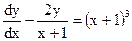
Задача 6. Группу из 25 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 4 человека, во вторую — 6 и в третью — 15. Сколькими способами это можно сделать.
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,9 возможного значения х1, математическое ожидание M(x) = 2,2 и дисперсия D(x) = 0,36.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =7-6i z2 = 3+2i
Задание 9. Вычислить пределы функций
1. 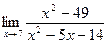 2.
2. 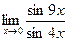
Вариант 7
Задание 1. Найдите A \ B, В \ А, (A \ B) ∪ (В \ А):
а) А = [–9; 4], B = (1; 6];
б) A = [3; 8]; B = [9; 11];
в) A = (–∞; 6]; B = (1; +∞).
Задание 2. Дан орграф. Построить матрицу смежности и инцидентности 
Задание 3. Вычислить неопределенные интегралы
1.  2.
2.  3.
3. 
Задание 4. Вычислить площадь фигуры, ограниченной линиями:

Задание 5. Найти частное решение дифференциального уравнения, удовлетворяющего указанным начальным условиям:
 y=1 при x=2
y=1 при x=2
Задача 6. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,8 возможного значения х1, математическое ожидание M(x) = 3,2 и дисперсия D(x) = 0,16.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =2-3i z2 = 1-4i
Задание 9. Вычислить пределы функций
1.  2.
2. 
Вариант 8
Задание 1. Даны множества A={2,3,7,10, 12} и B={1,3,7,8,10,13}
Найти: A∩B, AÈB, A\B, AΔB
Задание 2. Дан неориентированный граф. Построить матрицу смежности и инцидентности
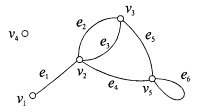
Задание 3. Вычислить неопределенные интегралы
1.  2.
2. 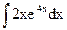 3.
3. 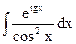
Задание 4. Вычислить площадь фигуры ограниченной линиями:
 ,
,  , y=0
, y=0
Задание 5. Найти частное решение дифференциального уравнения, удовлетворяющего указанным начальным условиям:
 y=0 при x=2
y=0 при x=2
|
|
|
Задача 6. Из 30 обучающихся группы надо выбрать старосту и помощника старосты. Сколькими способами это можно сделать?
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,6 возможного значения х1, математическое ожидание M(x) = 3,4 и дисперсия D(x) = 0,24.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =2-3i z2 = 1+9i
Задание 9. Вычислить пределы функций
1.  2.
2. 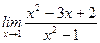
Вариант 9
Задание 1. Пусть заданы множества А, В и С такие, что А ∩ В = {5; 9},
А È В = {3; 4; 5; 9; 10; 11}, А ∩ C = {3}, C È В = {1; 2; 4; 5; 9; 11}.
Найдите множества A, B и С.
Задание 2. Дана матрица А. Построить соответствующий ей орграф, имеющий матрицу А своей матрицей смежности. Найти матрицу инцидентности для построенного орграфа. 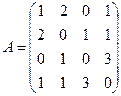
Задание 3. Вычислить неопределенные интегралы
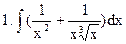
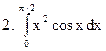 3.
3. 
Задание 4. Вычислить площадь фигуры ограниченной линиями:

Задание 5. Найти частное решение дифференциального уравнения, удовлетворяющего указанным начальным условиям:
 y=-1 при x=2
y=-1 при x=2
Задание 6. Сколькими способами могут занять I, II, III места 8 участниц финального забега на дистанции 100 м?
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,4 возможного значения х1, математическое ожидание M(x) = 3,4 и дисперсия D(x) = 0,24.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =4+2i z2 = 3-4i
Задание 9. Вычислить пределы функций
1.  2.
2. 
Вариант 10
Задание 1. Найдите А ∪ В и А ∩ В, если А = {x | 5x – 15 < 0}, В = {x | 6x + 18 > 0}.
Задание 2. Дана матрица А. Построить соответствующий ей орграф, имеющий матрицу А своей матрицей смежности. Найти матрицу инцидентности для построенного орграфа. 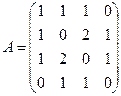
Задание 3. Вычислить неопределенные интегралы

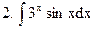

Задание 4. Вычислить площадь фигуры ограниченной линиями:  , y=0, x=1, x=4
, y=0, x=1, x=4
Задание 5. Найти частное решение дифференциального уравнения, удовлетворяющего указанным начальным условиям:
 y=1 при x=-2
y=1 при x=-2
Задача 6. Из аквариума, в котором 6 сазанов и 4 карпа, сачком выловили 5 рыб. Какова вероятность того, что среди них окажется 2 сазана и 3 карпа?
Задание 7. Найти закон распределения дискретной случайной величины, если известно, что дискретная случайная величина Х может принимать только два значения х1 и х2, причем х1 < х2; известна вероятность p1 = 0,2 возможного значения х1, математическое ожидание M(x) = 3,8 и дисперсия D(x) = 0,16.
Задание 8. Найти сумму, разность, произведение и частное двух комплексных чисел z1 и z2, если z1 =2+3i z2 = 1+9i
Задание 9. Вычислить пределы функций
1. 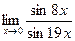 2.
2. 
|
|
|


