 |
Алгоритм подсчета критерия U Манна – Уитни.
|
|
|
|
Задание 2. Линейная корреляция
Дано корреляционное поле в виде таблицы
| 
| 
| 
| 
|
| 
| 
| 
| 
|
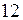
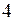
Вычислить коэффициент корреляции. Найти выборочное уравнение прямой регрессии Y на X, построить корреляционное поле и нанести на него линию прямой регрессии Y на X.
Решение. Определим выборочные средние значения для каждой случайной величины
, 
.
Найдем теперь значения исправленных выборочных дисперсий для каждой случайной величины
,
.
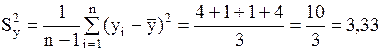Исправленная эмпирическая ковариация и коэффициент корреляции равны величинам
.
Эмпирический коэффициент регрессии Y на X находится по формуле
.
Уравнение прямой регрессии Y на X записывается в следующем виде
.
Рис.2. Корреляционное поле и линия регрессии Y на X.
Задание 3. Статистическая проверка статистических гипотез
Приведено эмпирическое распределение дискретной случайной величины 
в виде таблицы. Случайная величина имеет смысл числа отказов. Частоты наблюдений отказов обозначены 
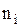. Используя критерий 
, проверить на уровне значимости 
гипотезу о распределении генеральной совокупности по закону Пуассона.
Решение. Дана таблица
|
| 
| 
| 
|
| 
|
|
| 
|
|
|
|
|
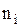
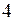
Найдем объем выборки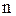 
по формуле
.
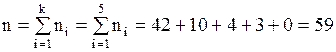Число 
описывает число групп данных, приведенных в таблице наблюдений.
Вычислим оценку параметра распределения 
в законе для редких событий Пуассона
.
Формула Пуассона закона распределения вероятностей имеет следующий вид
,
где 
– число появлений заданного события, в нашем примере это число отказов.
Проведем расчеты вероятностей
.
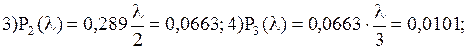
Найдем теоретические частоты 
, 
применяя расчетную формулу
,
в которой величина 
означает номер группы данных в таблице отказов. Подставим теоретические частоты в таблицу расчета эмпирического критерия Пирсона
|
|
|
|
|
| 
| 
|
|
| 
| 
| 
|
|
| 
|
| 
|
|
| 
| 
| 
|
|
| 
| 
| 
|
|
| 
|
|
|
| 
|
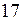
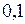
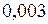
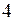
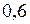
Эмпирический критерий находится путем суммирования данных, размещенных в последнем столбце таблицы расчета критерия Пирсона
,
где 
– общее число значимых групп данных.
Воспользуемся таблицами теоретического распределения, которое является функцией двух переменных (
– уровня значимости и числа степеней свободы 
)
Поскольку выполнено неравенство
,
то статистическую гипотезу о том, что генеральная совокупность распределена по закону редких событий Пуассона следует отвергнуть. При этом риск отвергнуть правильную гипотезу равен уровню значимости, т.е. в примере этот риск равен пяти процентам.
Задание 4. Доверительные интервалы для параметров нормального закона распределения
Найти с надежностью 
доверительный интервал оценки неизвестного математического ожидания 
для нормально распределенного признака 
, если даны значения: генеральное среднее квадратичное отклонение 
; выборочное среднее 
; объем выборки 
.
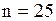Решение. Неизвестное математическое ожидание находится в интервале 
.
Последняя в записи формула обозначает уравнение относительно t, содержащее функцию Лапласа 
:
,
Применяя таблицы функции Лапласа, находим неизвестное значение параметра 
. Определим величину 
.
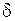
Найдем доверительный интервал
.
Доверительный интервал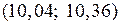 
покрывает математическое ожидание для нормально распределенной случайной величины с заданной величиной надежности 
, которая называется также доверительной вероятностью. В данной задаче доверительная вероятность равна 0,99 или 99%.
Задание 5
Решим задачу со следующими данными: n=32, n1=6, n2= 6, n3= 16 и n4= 4.
Отнесем к 1-му разряду тех студентов, которые получили 5 баллов (6 человек), ко 2-му разряду – 4 балла (6 человек), к 3-му – 3 балла (16 человек) и к 4-му – тех, кто получил 2 балла (4 человека). Если бы в каждом разряде было одинаковое количество студентов, то распределение оценок было бы равномерным. Сформулируем гипотезы:
|
|
|
Н0: Распределение оценок, полученных студентами по контрольной работе, не отличается от равномерного распределения.
Н1: Распределение оценок, полученных студентами по контрольной работе, статистически достоверно отличается от равномерного распределения.
Вычислим теоретическую частоту по формуле: fтеор = n/k, где n– количество наблюдений, k – количество разрядов. В нашем случае: fтеор = 32/4 = 8. Сравним с этой частотой все эмпирические частоты. Составим таблицу и все вычисления выполним в ней.
Таблица
| Разряды (количество баллов) | Эмпирические частоты fj | Теоретическая частота fт | fj – fт | (fj – fт)2 | (fj – fт)2/fт |
| 1 (5 баллов) 2 (4 балла) 3 (3 балла) 4 (2 балла) | -2 -2 -4 | 0.5 0.5 | |||
| Суммы |
Вычислим число степеней свободы n = к-1 = 4-1 = 3. Найдем по таблице критические значения: c2кр = 7.815 для a = 0.05, c2кр = 11.345 для a = 0.01. В соответствии с правилом принятия решения гипотезу Н0 следует отвергнуть. Распределение полученных оценок отличается от равномерного, но так как c2эмп < 11.345, статистически достоверно утверждать, что перед нами – группа «троечников» мы не можем.
Задание 6.
В таблице (ниже) представлены значения вербального интеллекта, полученные у студентов-физиков и студентов-психологов. Превосходят ли студенты-психологи студентов-физиков по уровню вербального интеллекта?
Алгоритм подсчета критерия U Манна – Уитни.
1. Представить все данные испытуемых из двух выборок объемами n1 и n2 в порядке возрастания (убывания).
2. Проранжировать все значения, не считаясь с тем, к какой выборке они относятся.
3.Подсчитать сумму рангов отдельно для каждого ряда. Проверить, совпадает ли общая сумма рангов с расчетной.
4. Определить большую из двух ранговых сумм.
5. Вычислить значение U эмп по формуле: U эмп = n1 n2 + nx (nx + 1)/2 – Tx, где nx – количество испытуемых в группе с большей суммой рангов, Tx – большая из двух ранговых сумм.
6. Определить критические значения U 0.05 по таблице. Если U эмп > U 0.05, то гипотеза H0 принимается. Если U эмп ³ U 0.05, то гипотеза H0 отвергается.
|
|
|
Теперь вернемся к поставленной задаче.
Таблица
Значения вербального интеллекта в выборках студентов физического и психологического факультетов
| Студенты – физики | Студенты – психологи | ||
| № испытуемого | Показатель интеллекта | № испытуемого | Показатель интеллекта |
Решение. Построим новую таблицу.
Таблица 7
| Студенты – физики | Студенты – психологи | ||||
| № исп. | Показатель интеллекта | Ранг | № исп | Показатель интеллекта | Ранг |
| 20.5 20.5 15.5 11.5 11.5 11.5 6.5 4.5 | 15.5 11.5 6.5 4.5 | ||||
|
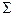
Общая сумма рангов: 165 + 186 = 351. Расчетная сумма:
SRi = N(N + 1)/2 = 26(26 + 1)/2 = 351.
Проверка выполнена. Из таблицы 7 видно, что большая ранговая сумма приходится на выборку студентов–психологов. Теперь сформулируем гипотезы:
H0: студенты-психологи не превосходят студентов-физиков по уровню вербального интеллекта;
H1: студенты-психологи превосходят студентов-физиков по уровню вербального интеллекта.
В соответствии с шагом 5 алгоритма вычисляем U эмп:
U эмп = 14×12 + 12 (12 + 1)/2 – 186 = 60.
По таблице критических значений для n1 = 12 и n2 = 14 находим U 0.05 = 51 и, в соответствии с правилом, гипотезу H0 принимаем. Студенты-психологи не превосходят студентов-физиков по уровню вербального интеллекта.
Литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика-М.: Высш.шк., 2003.- 210 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике -М., Высшее образование, 2006.- 21 с.
3.Сидоренко Е.В. Методы математической обработки в психологии / Е.В. Сидоренко. – С.-Петербург: Речь, 2001. – 349 с.
|
|
|
4. Белушкина Г.В. Математические модели и обработка эксперимента в психологии: учеб. пособие для вузов / Г.В. Белушкина, С.Н.Яременко. – Ростов н/Д: Издательский центр ДГТУ, 2010. – 101 с.
|
|
|
