 |
Алгебраическое решение поставленной задачи
|
|
|
|
В связи с тем, что модель была предварительно сбалансирована (Q=V), то отсюда следует, что одно уравнение является зависимым и транспортная модель содержит m+n-1 (2+5-1)=6 независимых уравнений и начальное базисное допустимое решение должно иметь 6 базисных переменных.
Для нахождения начального базисного допустимого решения используем процедуру, основанную на правиле северо-западного угла.
Начальное решение:
| V1 | V2 | V3 | V4 | V5ф | ∑Q | |
| Q1 | 50 8.8 | 50 0.6 | 50 1.3 | 10 1.9 | 0 | |
| Q2 | 2 | 2.5 | 0.3 | 90 0.7 | 30 0 | |
| ∑V |
Базисные переменные принимают значения: x11=50, x12=50, x13=50, х14=10, х24=90, х25=30 -остальные небазисные переменные равняются 0. Для полученного плана затраты на трелевку составят:
Y=8,8*50+0,6*50+1,3*50+1,9*10+0,7*90+0*30=617 у.е. в смену.
Оптимален ли этот план? На этот вопрос дает ответ условие оптимальности симплекс-метода (наличие положительных коэффициентов при небазисных переменных транспортной таблицы).
Первая итерация:
1)Нахождение вводимой в базис переменной (метод потенциалов):
x11=u1+v1=C11=8,8
x12=u1+v2=C12=0,6
x13=u1+v3=C13=1,3
x14=u1+v4=C14=1,9
x24=u2+v4=C24=0,7
x25=u2+v5=C25=0
Полагаем, что u1=0, тогда: v1=8,8, v2=0,6, v3= 1,3, v4=1,9, v5=1,2, u2=-1,2.
Оценки потенциалов небазисных переменных:
x15: C15=u1+v5-c15=0+1,2-0=1,2
x21: C21= u2+v1- с 21 =-1,2+8,8-2=5,6
x22: C22= u2+v2-c22 =-1,2+0,6-2,5=-3,1
x23: C23= u2+v3-c23 =-1,2+1,3-0,3=-0,2
Небазисная переменная x21, имеющая максимальную положительную оценку С21, выбирается в качестве вводимой в базис.
2) Нахождение переменной, выводимой из базиса. Последовательность обхода следующая: x21 – x11 – x14 – x24 – х21.
| V1 | V2 | V3 | V4 | V5ф | ∑Q | |
| Q1 |   - 50 8.8
| 50 0.6 | 50 1.3 |  + 10 1.9
| 0 | |
| Q2 |  + Х21 2
| 2.5 | 0.3 | - 90 0.7 | 30 0 | |
| ∑V |
Выводим из базиса x11=50, тогда значение х21=50 и транспортная задача имеет вид:
|
|
|
| V1 | V2 | V3 | V4 | V5ф | ∑Q | |
| Q1 | 8.8 | 50 0.6 | 50 1.3 | 60 1.9 | 0 | |
| Q2 | 50 2 | 2.5 | 0.3 | 40 0.7 | 30 0 | |
| ∑V |
Для полученного плана затраты на трелевку составят:
У=2*50+0,6*50+1,3*50+1,9*60+0,7*40+0*30=337 у.е. в смену.
Оптимальность нового решения определяется вычислением новых потенциалов:
x12=u1+v2=C12=0,6
x13=u1+v3=C13=1,3
x14=u1+v4=C14=1,9
x21=u2+v1=C21=2
x24=u2+v4=C24=0,7
x25=u2+v5=C25=0
Полагаем, что u1=0, тогда: v1=3,2, v2=0,6, v3=1,3, v4= 1,9, v5= 1,2, u2=-1,2.
Оценки потенциалов небазисных переменных:
x11: C11=u1+v1-c11=0+3,2-8,8=-5,6
x15: C15= u1+v5-c15 = 0+1,2-0= 1,2
x22: C22= u2+v2-c22 = -1,2+0,6-2,5=-3,1
x23: C23= u2+v3-c23=-1,2+1,3-0,3=-0,2
Небазисная переменная x15, имеющая максимальную положительную оценку С21, выбирается в качестве вводимой в базис.
3) Нахождение переменной, выводимой из базиса. Последовательность обхода следующая: x15 – x25 – x24 – x14 – х15.
| V1 | V2 | V3 | V4 | V5ф | ∑Q | |
| Q1 | 8.8 | 50 0.6 | 50 1.3 |   - 60 1.9
|  + x15 0
| |
| Q2 | 50 2 | 2.5 | 0.3 |  + 40 0.7
| - 30 0 | |
| ∑V |
Выводим из базиса x25=30, тогда значение х15=30 и транспортная задача имеет вид:
| V1 | V2 | V3 | V4 | V5ф | ∑Q | |
| Q1 | 8.8 | 50 0.6 | 50 1.3 | 30 1.9 | 30 0 | |
| Q2 | 50 2 | 2.5 | 0.3 | 70 0.7 | 0 | |
| ∑V |
Для полученного плана затраты на трелевку составят:
У=2*50+0,6*50+1,3*50+1,9*30+0,7*70+0*30=301 у.е. в смену.
Оптимальность нового решения определяется вычислением новых потенциалов:
x12=u1+v2=C12=0,6
x13=u1+v3=C13=1,3
x14=u1+v4=C14=1,9
x15=u1+v5=C15=0
x21=u2+v1=C21=2
x24=u2+v4=C24=0,7
Полагаем, что u1=0, тогда: v1=3,2, v2=0,6, v3=1,3, v4= 1,9, v5= 0, u2=-1,2.
Оценки потенциалов небазисных переменных:
x11: C11=u1+v1-c11=0+3,2-8,8=-5,6
x22: C22= u2+v2-c22 = -1,2+0,6-2,5=-3,1
x23: C23= u2+v3-c23=-1,2+1,3-0,3=-0,2
x25: C25= u2+v5-c25=-1,2+0-0=-1,2
В соответствии с условием оптимальности можно сделать вывод о достижении оптимального решения. Полученный план трелевки обеспечит минимальные затраты. При этом сменные маршруты и соответствующие объемы трелевки примут следующий вид:
50 м3 по маршруту с первой лесосеки на второй погрузочный пункт;
50 м3 по маршруту с первой лесосеки на третий погрузочный пункт;
|
|
|
30 м3 по маршруту с первой лесосеки на четвертый погрузочный пункт;
50 м3 по маршруту со второй лесосеки на первый погрузочный пункт;
70 м3 по маршруту со второй лесосеки на четвертый погрузочный пункт;
30 м3 по маршруту с первой лесосеки на пятый погрузочный пункт (фиктивный)
Суммарные затраты (себестоимость) на трелевку при этом плане составят 301 у.е.
Компьютерное решение поставленной задачи в математической программной среде Excel
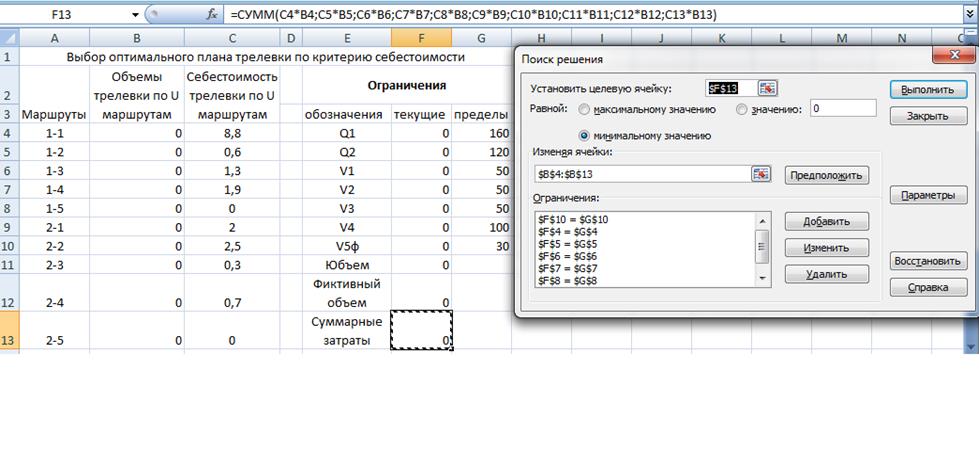Рис.1. Исходная постановка транспортной задачи в Excel.
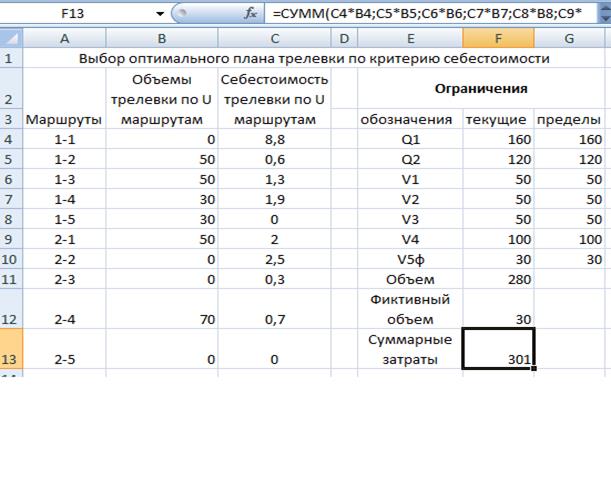
Рис.2. Результаты оптимального решения транспортной задачи в Excel.
Список используемой литературы
1. Редькин А.К. Математическое моделирование и оптимизация технологий лесозаготовок: учебник для вузов/ А.К.Редькин, С.Б.Якимович. -М.:ГОУ ВПО МГУЛ, 2005.-504 с.
2. Основы моделирования и оптимизации процессов лесозаготовок: Задания и методические указания по выполнению расчетно-графических и лабораторных работ с приминением ЭВМ для студентов специальности 26.01/Сост. С.Б.Якимович.- Йошкар-Ола: МарПИ, 1990.-60 с.
|
|
|
