 |
Условие постоянства функции. Условия монотонности функции.
|
|
|
|
ОКРЕСТНОСТЬ. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКЕ И БЕСКОНЕЧНОСТИ. ОДНОСТОРОННИЕ ПРЕДЕЛЫ.






БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ, ИХ СВОЙСТВА. ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИИ. ЕДИНСТВЕННОСТЬ ПРЕДЕЛА.
Бесконечно малые





Бесконечно большие



Основные теоремы








Теорема. Если функция или последовательность имеет предел, то он единственен.
ОСОБЫЕ СЛУЧАИ ПРЕДЕЛОВ СУММЫ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО. НЕОПРЕДЕЛЕННОСТИ. СПОСОБЫ РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТЕЙ. ПРИМЕРЫ.

Непосредственная подстановка:


Разложение на множители:


Умножение на сопряженное:


Почленное деление числителя и знаменателя на степень многочлена в знаменателе







ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ И СЛЕДСТВИЕ ИЗ НЕГО. ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ И СЛЕДСТВИЯ. СРАВНЕНИЯ БЕСКОНЕЧНО МАЛЫХ. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ. ЗАМЕНА БЕСКОНЕЧНО МАЛЫХ ИХ ЭКВИВАЛЕНТНЫМИ ПРИ ВЫЧИСЛЕНИИ ПРЕДЕЛОВ.
Первый замечательный предел: 

Второй замечательный предел 





НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ, НЕПРЕРЫВНОСТЬ В ТОЧКЕ СЛЕВА И СПРАВА. ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ.

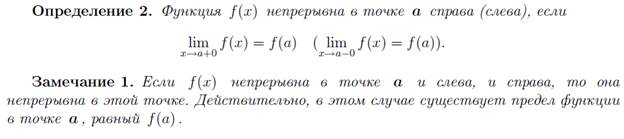



6. ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ.


ФУНКЦИИ, НЕПРЕРЫВНЫЕ НА ОТРЕЗКЕ. СВОЙСТВА ФУНКЦИЙ НА ОТРЕЗКЕ (ТЕОРЕМЫ ВЕЙЕРШТРАССА И БОЛЬЦАНО - КОШИ).


Теорема Вейерштрасса: если функция непрерывна на отрезке, то она ограничена на нем.
Теорема Больцано-Коши: если функция может принимать два значения, то она может принимать и любое значение между ними.
ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. КОНЕЧНЫЕ И БЕСКОНЕЧНЫЕ ПРОИЗВОДНЫЕ. ОДНОСТОРОННИЕ ПРОИЗВОДНЫЕ, ИХ СВЯЗЬ С ПРОИЗВОДНОЙ. МЕХАНИЧЕСКИЙ И ГЕОМЕТРИЙ СМЫСЛ ПРОИЗВОДНОЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ.
|
|
|



Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, что производная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.

Геометрический смысл:


Физический смысл:



ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ. НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ ДИФФЕРЕНЦИРУЕМОСТИ. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ФУНКЦИЙ. ДИФФЕРЕНЦИРОВАНИЕ ОБРАТНОЙ ФУНКЦИИ. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ.

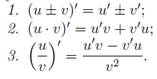


10. ПРОИЗВОДНЫЕ ФУНКЦИЙ:
11. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
12. ПРОИЗВОДНЫЕ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
Непонятно, что имеется ввиду. Видимо, вывод производных этих функций(см. лекцию 6, 7)
ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ. ПРОИЗВОДНАЯ СТЕПЕННО-ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ.


ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИИ И НЕЯВНО.
Параметрически
 Неявно
Неявно

ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ. МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ ВТОРОГО ПОРЯДКА. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ И НЕЯВНО.





УРАВНЕНИЕ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ.
ДИФФЕРЕНЦИАЛ И ЕГО СВЯЗЬ С ПРОИЗВОДНОЙ. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ.





ДИФФЕРЕНЦИАЛ СЛОЖНОЙ ФУНКЦИИ. ИНВАРИАНТНАЯ ФОРМА ДИФФЕРЕНЦИАЛА. ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ. НАРУШЕНИЕ ИНВАРИАНТНОЙ ФОРМЫ ЗАПИСИ ДИФФЕРЕНЦИАЛОВ ВЫСШИХ ПОРЯДКОВ.



ТЕОРЕМА ФЕРМА И РОЛЛЯ, ИХ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ.

Геометрический смысл теоремы состоит в том, что в точке экстремума касательная к кривой параллельна оси абсцисс



ТЕОРЕМА ЛАГРАНЖА, ЕЕ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ТЕОРЕМА КОШИ.





ПРАВИЛО ЛОПИТАЛЯ.
|
|
|

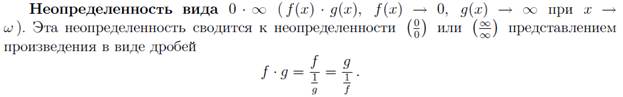


УСЛОВИЕ ПОСТОЯНСТВА ФУНКЦИИ. УСЛОВИЯ МОНОТОННОСТИ ФУНКЦИИ.
Условие постоянства

Условие монотонности

23. ПОНЯТИЕ МАКСИМУМА И МИНИМУМА ФУНКЦИИ. НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА. ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА (ПО ПЕРВОЙ ПРОИЗВОДНОЙ). ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА (ПО ВТОРОЙ ПРОИЗВОДНОЙ). 




|
|
|


