Подсчитать радиус основной шайбы кулачка, приняв минимальный радиус кривизны профиля кулачка

R_{крив.min .}=(10…20) 10^-3 м

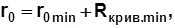Если минимальный радиус r_0min получается меньше, чем ход толкателя h_max, то следует принять

r ₀ =(3…5) h_max.

Построить в масштабе теоретический профиль кулачка, применив метод обращенного движения. Для этого от произвольного положения против вращения отложим фазовые углы φ_п, φ_вв, φ_оп. Разбиваем фазовые углы на интервалы, соответствующие интервалам закона движения и проводим оси толкателя как центральные, проходящие через центр ращения кулачка. По соответствующим направлениям откладываем перемещения толкателя s_i при этом рекомендуется заполнить таблицу. Выделить кружочками центры тарелки во всех промежуточных положениях тол­кателя.

Положения

S диаграммы

Перемещение на плане

Положения

S диаграммы

Перемещение на плане

 

Построить практический профиль кулачка, проводя перпендикуляры к радиусам (тарелки) через соответствующие точки теоретического профиля. Действительный профиль будет являться огибающей параметрического семейства тарелок.

Выбрать радиус тарелки толкателя, учитывая, что величи­на радиуса тарелки должна быть R_{тарелки}›│ds/dφ│_max.

Радиус тарелки R_тар толкателя может быть определен и приближенно после построения практического профиля кулачка по расстоянию от центра тарелки до наиболее удаленной точки касания тарелки с практическим профилем. Радиус тарелки следует принять на (5..8)х10^-3м большим, чем найденное расстояние с учетом масштаба построения.

R_{тарелки}=│ds/dφ│_max +5…8 мм.

 

Закончить построение плана кулачкового механизма с та­рельчатым толкателем. показав контурной линией практический профиль кулачка, пунктирной линией теоретический профиль. В одном из положений изобразить тарельчатый толкатель с учетом определенного радиуса тарелки R_тар, показать опоры кулачка и толка­теля. Проставить на плане механизма r₀, h_max, ω_кул, углы φ_п, φ_вв, φ_оп, φ_нв, а также обозначить номера всех взаимных положений кулачка и толкателя.

 

ЛИСТ 2

ПРОЕКТИРОВАНИЕ ЗУБЧАТОЙ ПЕРЕДАЧИ

 

 

Цель листа. Для заданных параметров цилиндрической зубчатой передачи провести геометрический расчет и выполнить чертеж эвольвентной цилиндрической зубчатой передачи внешнего зацепления. Определить также качественные показатели этой передачи.

Пример выполнения листа показан на Рис. 4

 

2.1. Исходные данные

 

Исходные данные для выполнения второго листа содержатся на странице задания.

Z_1, Z_2, - числа зубьев колес

m – модуль зубчатой передачи

x₁, x₂ – коэффициенты смещения инструмента при нарезании

зубчатых колес

Параметры исходного контура (ГОСТ 13755-84)

h_a^*- коэффициент высоты головки зуба

h_l^*- коэффициент граничной высоты

с^* - коэффициент радиального зазора

α- угол профиля исходного контура

 

2.2 Расчет основных геометрических параметров

1. Делительное межосевое расстояние

а=(z₁+z₂)m/2

2. Коэффициент суммы смещений

x_S=x₁+x₂

 

3. Угол зацепления

inva_W= inva+2x_Stana/(z₁+z₂)

a_W=

Величина угла зацепления α_w может быть определена по таблицам инвалют или рассчитана на калькуляторе методом последовательных приближений.

Например подсчитанное значение inv α_w =0,034956. Найдем α_w.

Напомним, что специальная функция инволюта угла α равна inv α=tan α – α, где α подставляется в радианах. Например 20 град=0,3490658 рад.

inv 20= inv 0,3490658=tan 0,3490658 –0,3490658= 0,01490438

Выберем диапазон α, внутри которого наверняка лежит угол зацепления α_w. Например: 20⁰ и 30⁰. Подсчитаем на калькуляторе, по приведенной формуле, инволюты этих углов.

inv 20⁰ =0,014904, inv 30⁰= 0,0537515.

Делим диапазон α попалам и ищем инволюту 25⁰

inv 25⁰ =0,029975, меньше чем 0,034956, следовательно α_w лежит между 25⁰ и 30⁰.

Берем 26⁰, ищем инволюту

inv 26⁰ =0,0339469, меньше чем 0,034956, следовательно опять α_w лежит между 26⁰ и 30⁰. Берем 26,3⁰, ищем инволюту

inv 26,3⁰ =0,0352092, чуть больше чем 0,034956.

Немного уменьшаем угол при приближении и т.д.

 

 

 

 

inv 26,25⁰ = 0,0349965

inv 26,245⁰ = 0,034975

inv 26,243⁰ = 0,0349667

inv 26,2425⁰ =0,03496467

inv 26,242⁰ = 0,034962

inv 26,2414⁰ =0,03496 Точность достаточная.

4. Межосевое расстояние

a_w=(z₁+z₂) m cosa /(2cosa_w)

5. Делительный диаметр шестерни и колеса

d₁=z₁m

d₂=z₂m

6. Передаточное число

u=z₂/z₁

7. Начальный диаметр шестерни и колеса

d_w1=2a_w/(u+1)

d_w2=2a_w u/(u+1)

8. Коэффициент воспринимаемого смещения

y=(a_w- a)/m

9. Коэффициент уравнительного смещения

Dy= x_S - y

10.Диаметр вершин зубьев шестерни и колеса

d_a1=d₁+2(h_a^*+ x₁-Dy)m

d_a2=d₂+2(h_a^*+ x₂-Dy)m

11. Диаметр впадин шестерни и колеса

d_f1=d₁-2(h_a^*+ c^*- x₁)m

d_f2=d₂-2(h_a^*+ c^*- x₂)m

II. Проверка расчетов, выполненных по пунктам 1-11

12. Межосевое расстояние

a_w=r_w1+r_w2

a_w=r₁+r₂ +ym

a_w=r_a1+r_f2 +c^*m

a_w=r_f1+r_a2 +c^*m

2.3 Расчет вспомогательные геометрических параметров

13. Основной диаметр шестерни и колеса

d_b1=d₁cosa

d_b2=d₂cosa

14. Угловой шаг зубьев шестерни и колеса

t₁=360⁰/z₁

t₂=360⁰/z₂

15. Хорда делительной окружности, соответствующая угловому шагу зубьев шестерня и колеса

Р₁=d₁sin(t₁/2)

Р₂=d₂sin(t₂/2)

16. Окружная толщина зуба по делительной окружности шестер­ни и колеса

S₁=(p/2+2 x₁ tga)m

S₂=(p/2+2 x₂ tga)m

17. Высота зуба (глубина врезания инструмента в заготовку)

h=(d_a1-d_f1)/2

h=(d_a2-d_f2)/2

h=(2h_a^*+c^*-Dy)m

18. Угол профиля зуба в точка на окружности вершин шестерни α_а1 и колеса α_а2.

сosa_a1=d_b1/d_a1 a_a1=

сosa_a2=d_b2/d a_a2=

19. Радиус кривизны активного профиля зуба в нижней точке шестерни и колеса

r_p1=a_wsina_w – r_b2tga_a2

r_p2=a_wsina_w – r_b1tga_a1

20. Угол развернутости активного профиля зуба в нижней точ­ке шестерни и колеса

n_р1=2r_p1/d_b1

n_р2=2r_p2/d_b2

21. Шаг зацепления

P_a=pmcosa

2.4 Проверка качества зацепления по геометрическим показателям

22. Коэффициент наименьшего смещения (проверка отсутствия подрезания зуба) шестерни и колеса

x_min1=h_e^* - h_a^* - (z₁sin²a)/2

x_min2=h_e^* - h_a^* - (z₂sin²a)/2

Сделать заключение о работоспособности передачи, сравнив коэффициент наименьшего смещения с заданным.

При x₁> x_min1 подрезание зуба шестерни отсутствует.

При x₂> x_min2 отсутствует подрезание зуба колеса.

При сравнении коэффициентов смещения подставить цифровые значения для колеса и шестерни.

23. Радиус кривизны в граничной точке профиля зуба (провар­ка отсутствия интерференции зубьев) шестерни и колеса

r_е1=d₁sina/2 – (h_e^* - h_a^*-x₁)m/sina

r_е2=d₂sina/2 – (h_e^* - h_a^*-x₂)m/sina

Дать заключение о наличии или отсутсвии интерференции зубьев. При r_е1 < r_p1 и r_е2 < r_p2 интерференция зубьев отсутствует. При r_е<0 происходит подрезание зуба. Заключение обосновать,подставив цифровые значения.

24. Коэффициент торцового перекрытия

e_a=[z₁tga_a1 + z₂tga_a2 – (z₁+z₂)tga_w]/2p

ГОСТ 16532-70 рекомендует для прямозубых передач иметь e_a>1,2

25. Нормальная толщина зуба на окружности вершин

S_a1=[p/2+2x₁tga+z₁(inva-inva_a1)]mcosa/cosa_a1

S_a2=[p/2+2x₂tga+z₂(inva-inva_a2)]mcosa/cosa_a2

Дать заключение о работоспособности зубчатых колес. Гост 16532-70 рекомендует иметь S_a > 0,3m при однородной структуре материала зубьев и S_a > 0,4m при поверхностном упрочнении зубьев. Заключение обосновать, подставив цифровые значения.

 

2.5 Проверка качества зацепления по удельному скольжению

 

Качество зацепления оценивается по максимальному удельному скольжению в контактной точке профиля зуба при движении общей точки по всей длине активной линии зацепления. Скорости общей точки К по эвольвентному профилю в направлении скольжения для шестерни и колеса пропорциональны расстояниям r_k1и r_k2 точки контакта К от точек N₁ и N2. Эта скорость равна тангенциальной составляющей точки контакта.

V^t_k1=w₁l_N1к=w₁r_k1

V^t_k2=w₂l_N2к=w₂r_k2

При построении графиков зависимостей V^t_k1 и V^t_k2 воспользуемся равенством этих скоростей в полюсе Р. Эту скорость следует изобразить любым отрезком PВ, проведенным из полюса Р.

Прямые, исходящие из точек N₁ и N₂ и проходящие через В дают зависимости V^t_{k1 и} V^t_k2.

Графики этих зависимостей (в масштабах для ско­ростей) для всей длины линии зацепления N₁N₂ необходимо построить на листе чертежа зубчатой передачи.

 

 

 

 

Рис. 5 Диаграммы тангенциальных составляющих скоростей точек контакта V^t_к1 и V^t_к2 вдоль теоретической линии зацепления.

 

27. Удельное скольжение контактной точки эвольвентного профиля шестерни и колеса помещаем в таблицу

 

q₁₂= (V^t_k1- V^t_к2)/ V^t_k1 = (у₁-у₂)/у_1; q₂₁= (V^t_к2 - V^t_k1)/ V^t_к2 = (у₂-у₁)/у_2;

 

Для вычисления удельного скольжения рекомендуется исходные данные и результаты записать в таблицу.

 

 

У1

У2

У1-У2

q12

У2-У1

q21

 

В число расчетных положений необходимо включить начальную контактную точку профилей зубьев А и конечную контактную точку профилей зубьев В, полученные от пересечения окружностей вершин обоих колес с линией зацепления N₁N_2.

 

 

2.6 Выполнение чертежа зубчатой передачи.

 

В соответствии с заданием вычертить внешнее зацепление и показать не менее трех зубьев на каждом колесе Рис 4. Масштаб чертежа выбрать таким, чтобы

полная высота зуба на чертеже была около 60 мм. Исходя из этих условий

задаемся масштабом М

Зацепление колес вычертить с обозначением всех элементов и размеров зацепления. Провести линию центров, пометить на ней центры О₁, О₂ обоих колес, отметить положение полюса Р на линии центров в точке соприкосновения начальных диаметров шестерни и колеса. Чертим дуги соответствующих начальных окружностей. Далее начертить делительные, основные окружности а также окружности вершин и впадин. Через полюс зацепления Р провести касательную tt к начальным окружностям и линию зацепления N₁N₂. Она касается обеих основных окружностей в точках N₁ и N₂ соответственно и образует угол зацепления α_w с линией tt.

Строим две эвольвенты двух зубьев, проходящие чрез полюс Рис 6. Для этого делим линию зацепления N₁P на целое число отрезков(четыре, пять, шесть) и откладываем на основной окружности дуги, равные этим отрезкам помечая точки деления. Найдем начало эвольвенты на основной окружности. В предыдущей точке проводим касательную и откладывает отрезок один раз. Во второй точке два и так далее. В результате на касательных получим серию точек, соединив которые по лекалу построим эвольвенту. Аналогично поступаем с линией N₁P и построение второй эвольвенты.

Для построения трех зубьев на каждом колесе воспользуемся правилами симметричного отображения, величинами угловых шагов зацепления t₁ и t₂, шагом зацепления р_a и шагом на делительной окружности р, а также окружными толщинами зуба на делительной окружности s₁ и s₂ и нормальными толщинами на окружности вершин s_а1 и s_а2. На чертеже отметить угол зацепления α_w, теоретическую N₁N₂ и практическую АВ линии зацепления. В точках А и В пунктирной линией построить эвольвентные профили соответствующие моменту входа и выхода зубьев из зацепления. Показать также на действительной линии зацепления пунктирной линией по два эвольвентных профиля, отстоящие от А и В на шаг, тем самым показав зоны однопарного и двупарного зацепления. На чертеже показать дуги перекрытия а₁в₁ и а₂в₂ и соответствующие им углы перекрытия φ_γ1 и φ_γ2. Для точек А и В показать профильные углы при вершине зубьев шестерни и колеса. Показать шаги по начальной и основной окружности.

 

На листе чертежа поместить три таблицы.

 

Таблица исходных данных

Z1	Z2	m	α	hе*	ha*	c*	x1	x2
		мм	град

 

Таблица величин, характеризующих шестерню и колесо

da1

da2

d1

d2

db1

db2

df1

df2

h

s1

s2

sa1

sa2

миллиметры

 

 

Таблица величин, характеризующих зацепление

aw	αw	y	Δy	xmin1	xmin2	dw1	dw2	gα	εα	θ12	θ21
мм	град					мм	мм	мм
										От… до	От… до

 

Рис. 6

 

 

ЛИСТ № 3

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: