 |
Определение размерности Хаусдорфа фракталов с циклически повторяющимися структурами
|
|
|
|
С.С. Кубрин
Институт “Гипроуглеавтоматизация”, Кемерово
Классически, в литературе описание фракталов начинается с примера триадной кривой Гельгона фон Коха. Эта кривая строится итеративно. Построение начинается с прямолинейного отрезка единичной длины. На первом шаге исходный отрезок заменяется четырьмя длиной каждый в 1/3 от длины исходного. Далее, операция повторяется с каждым вновь полученным отрезком. Таким образом, получают кривую Коха разной детальности в зависимости от числа итераций 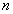 . Когда число итераций устремляется к бесконечности (
. Когда число итераций устремляется к бесконечности (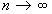 ) получаем предельную кривую (рис. 1).
) получаем предельную кривую (рис. 1).
Легко видеть, что длина триадной кривой Коха определяется формулой 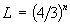 и стремится к бесконечности. Соответственно, размерность Хаусдорфа данного фрактального образования определяется соотношением:
и стремится к бесконечности. Соответственно, размерность Хаусдорфа данного фрактального образования определяется соотношением: 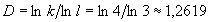 (
( - число элементов,
- число элементов, 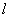 - относительный размер элементов).
- относительный размер элементов).

Для построения кривой Коха, используется только одна структура. К сожалению, такие фракталы в природе редко встречаются. Чаще всего, в построении фракталов участвуют несколько структур, состоящих из различного числа элементов. Причем, размеры элементов структур также различны.
Рассмотрим небольшой пример. Пусть элементы кривой (это, конечно, будет уже не кривая Коха) на первой итерации делятся на три элемента, на второй на четыре, в третьем на пять, в четвертом снова на три и так далее изменясь циклически. А правило определяющее размер элементов остается тем же, что и для кривой Коха.
Тогда, в самом начале процесса длина кривой определяется как 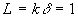 ; где:
; где: 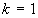 - число элементов,
- число элементов, 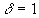 - длина элемента. На первом шаге (n=1) длина кривой и её форма не меняются
- длина элемента. На первом шаге (n=1) длина кривой и её форма не меняются 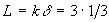 , (
, (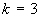 ,
, 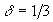 ).
).
Запишем число элементов кривой и длины элементов для следующих нескольких итераций. Так при:
|
|
|
n=2, 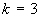 ,
, 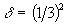 n=3,
n=3, 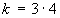 ,
, 
n=4, 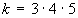 ,
, 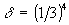 n=5,
n=5, 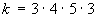 ,
, 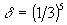
n=6, 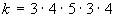 ,
, 
и соответственно для 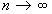 :n,
:n, 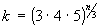 ,
, 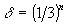 .
.
Итак, длина кривой будет равна  . Выражая n через длину элемента (
. Выражая n через длину элемента (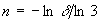 ) и применяя прямую и обратную операции логарифмирования имеем:
) и применяя прямую и обратную операции логарифмирования имеем:
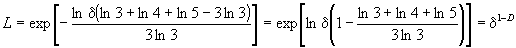 .
.
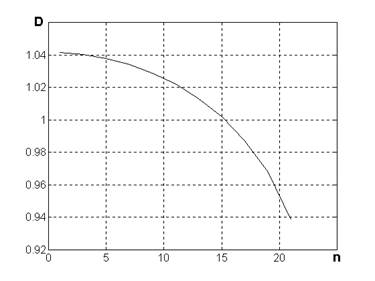
Рис.2. Влияние на размерность Хаусдорфа числа структур с различным
количеством элементов (l = 1/10). В точке n = 1 k = 11.
Откуда фрактальная размерность  . По сравнению с кривой Коха у вновь полученной кривой размерность Хаусдорфа меньше, но длина ее все еще не конечна. Обобщая полученный результат, на произвольное число структур, формула для определения размерность Хаусдорфа при циклическом структуроформирующем правиле примет вид:
. По сравнению с кривой Коха у вновь полученной кривой размерность Хаусдорфа меньше, но длина ее все еще не конечна. Обобщая полученный результат, на произвольное число структур, формула для определения размерность Хаусдорфа при циклическом структуроформирующем правиле примет вид:
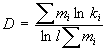 ,
,
здесь: å - число различных структур; 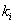 - число элементов в
- число элементов в 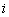 структуре;
структуре; 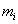 - число повторений
- число повторений 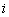 структуры.
структуры.
Произведя аналогичные рассуждения относительно правила, определяющего размер элементов структур, получим зависимость от числа структур и вариации размеров элементов структур:
 .
.
Проанализируем влияние численности структур, участвующих в формировании фрактального образования, на размерность Хаусдорфа этого образования. Пусть имеются несколько фрактальных образований. Первое строилось с помощью одной структуры, состоящей из j элементов. Второе – с помощью трех структур, состоящих соответственно из j-1, j и j+1 элементов. Третье – с помощью пяти структур, состоящих соответственно из j-2, j-1, j,j+1 и j+2 элементов. И так далее. На рис. 2 построен график зависимости размерности Хаусдорфа от числа структур. Из рисунка видно, что, чем больше разнообразность структур, тем меньше размерность 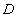 .
.
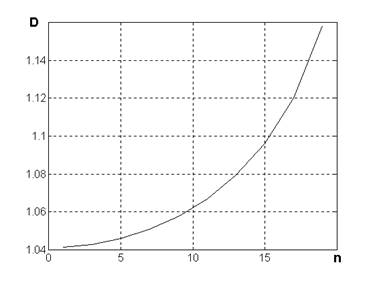
Рис.3. Влияние на размерность Хаусдорфа числа различных элементов в структуре (k = 11). В точке n = 1 l = 10.
Рис. 3 иллюстрирует влияние на размерность Хаусдорфа вариации размеров элементов в структуре. С увеличением количества размеров элементов, растет размерность 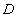 .
.
Анализ полученных результатов приводит к выводу, что вычисление размерности Хаусдорфа в сложных фрактальных образованьях осреднением числа или (и) длин элементов структур недопустимо. Прикладной интерес представляют фракталы с размерностью меньше размерности пространства.
|
|
|
Использование фракталов с циклически повторяющимися структурами позволяет легко получать самоподобные образование требуемой размерности, что необходимо в различных приложених.
Список литературы
Пайтген Х.О., Рихтер П.Х., Красота фракталов. Образы комплексных динамических систем, М.: Мир, 1993. 176 с.
Федер Енс. Фракталы. М.: Мир, 1991. 254 с.
Mandelbrot B.B., The Fractal Geometry of Nature. Freeman, SanFrancisco, 198
|
|
|


