 |
Условие прочности штифта на смятие
|
|
|
|
Выбираем клиновой ремень сечения А со следующими параметрами
| Тип ремня | Сече- ние | Вр, мм | В0, мм | h, мм | Y0, мм | А, мм | Предель-ные длины, мм | d1min, мм | Т1,

| Q,

|
| Нормальный клиновой ремень | А | 2,8 | 560…4000 | 11…70 | 0,10 |
Таблица 2 - Параметры клинового ременя
d1=90 мм
Диаметр ведомого шкива d2, мм
d2 = d1 ·U · (1-  ) (2.1)
) (2.1)
где  = 0,01 - коэффициент скольжения кордшнуровых ремней.
= 0,01 - коэффициент скольжения кордшнуровых ремней.
подставляя данные в формулу (2.1) получается:
d2=90·3· (1-0,01)=267,3 мм
Принимается d2=280 мм
Уточняем значение передаточного отношения
 (2.2)
(2.2)
подставляя данные в формулу (2.2) получается:

Межосевое расстояние аw
Принимаем с= 1, тогда
аw =d2 ·С (2.3)
подставляя данные в формулу (2.3) получается:
aw =280·1 = 280 мм
Принимаем 280 мм.
Длина ремня L
 (2.4)
(2.4)
подставляя данные в формулу (2.4) получается:
 Принимается L=1250 мм
Принимается L=1250 мм
С учётом стандартной длины уточняем межосевое расстояние
 (2.5)
(2.5)
подставляя данные в формулу (2.5) получается:


Принимаем аw=320 мм
Линейная скорость ремней 
 =
=  (2.6)
(2.6)
подставляя данные в формулу (2.6) получается:

[V]=25 м/с – допускаемая скорость для клиновых ремней.
Число пробегов ремня 
 (2.7)
(2.7)
Соблюдение соотношения V≤[V] условно выражает долговечность ремня и его соблюдение гарантирует срок службы ремня 1000…5000 часов.
[U]=20-допускаемое число пробегов для клиновых ремней
подставляя данные в формулу (2.7) получается:

Угол обхвата ремнями ведущего шкива по формуле (2.8)
 = 180 о-57.3 о· (d2 - d1 )/a (2.8)
= 180 о-57.3 о· (d2 - d1 )/a (2.8)
подставляя данные в формулу (2.8) получается:
 =180 о- 57.3 о· (280-90)/320=146 о
=180 о- 57.3 о· (280-90)/320=146 о
Т.к. допустимый угол обхвата [  ] =120 о, то условие
] =120 о, то условие 
 [
[  ] выполняется.
] выполняется.
Определение требуемого числа клиновых ремней.
Предварительно определяется допускаемая мощность [P], которую может передать в данных условиях эксплуатации один клиновой ремень по формуле (2.9)
|
|
|
 (2.9)
(2.9)
где Р0 – мощность, допускаемая на один ремень в типовых условиях: при  ;u=1, длине типового ремня –L0 и спокойной односменной работе, кВт Р0=1.75 кВт
;u=1, длине типового ремня –L0 и спокойной односменной работе, кВт Р0=1.75 кВт
коэффициент угла обхвата, 
 =0,92
=0,92
 коэффициент длины ремня,
коэффициент длины ремня,
 (2.10)
(2.10)
подставляя данные в формулу (2.10) получается:


 коэффициент передаточного отношения,
коэффициент передаточного отношения, 
 коэффициент режима нагрузки,
коэффициент режима нагрузки, 
подставляя данные в формулу (2.8) получается:

Определяем число зубьев по формуле (2.11)
 (2.11)
(2.11)
где 
подставляя данные в формулу (2.11) получается:

Принимаем 5 ремня
Определяется сила натяжения ремня F0 (Н) для одного клинового ремня по формуле (2.13):
F0= 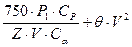 (2.12)
(2.12)
Где:
Θ=0,10 Н·с2/м2
подставляя данные в формулу (2.11) получается:
F0=  H
H
где:
Р1= 5.5 кВт – номинальная мощность электродвигателя в номинальном режиме работы.
Радиальное усилие, действующее на вал клиноремённой передачи:
Fr=2•F0·Z·sin(α1/2) (2.13)
подставляя данные в формулу (2.13) получается:
Fr=2•135•4•sin(146/2)=1032,8 H
3 Расчёт тихоходной передачи
3.1 Выбор твёрдости, термической обработки, материала
 Для изготовления шестерни и колеса принимаем сталь 40Х, механические характеристики которой после улучшения приведены в таблице (3).
Для изготовления шестерни и колеса принимаем сталь 40Х, механические характеристики которой после улучшения приведены в таблице (3).
Таблица 3 - Характеристики стали 40Х
| Шестерня: | Колесо: | |
| Термическая обработка: | Поверхностная закалка | Объемная закалка |
| Твёрдость сердцевины: | НВ269…302 | НВ269…302 |
| Твёрдость поверхности: | HRC40..56 | HRC38-50 |
| Предел текучести σТ: | 750 МПа | 750 Мпа |
| Dпред | 125 мм | |
| Sпред | 80 мм |
3.2 Проверочный расчёт
Допускаемые контактные напряжения шестерни:
[σ]Н1=17•HRC+200=17•(40…56)+200=1016 МПа (3.2.1)
Допускаемые контактные напряжения колеса:
[σ]Н2=17•HRC+100=17•(38…50)+100=848 МПа (3.2.2)
Допускаемые напряжения изгиба шестерни:
[σ]F1=500 МПа
Допускаемые напряжения изгиба колеса:
[σ]F2=700 МПа
Расчётное допускаемое контактное напряжение:
|
|
|
[σ]H=[σ]Hlim  (3.2.3)
(3.2.3)
где
[σ]Hlim-предел контактной выносливости
SH=1,1- коэффициент запаса прочности
ZN- коэффициент долговечности
ZR- коэффициент, учитывающий шероховатость поверхности зубьев
ZV- коэффициент, учитывающий окружную скорость
Произведение ZR и ZV принимаем равным 1
 (3.2.4)
(3.2.4)
NHO-базовое число циклов нагружения
NHE-расчетное число циклов нагружения
 (3.2.5)
(3.2.5)  (3.2.6)
(3.2.6)
подставляя данные в формулу (3.2.6) получается:
 часа
часа
подставляя данные в формулу (3.2.5) получается:


с=1-число колес, находящихся в зацеплении
 Т.к NHE>NHO,то принимаем ZN=1
Т.к NHE>NHO,то принимаем ZN=1
подставляя данные в формулу (3.2.3) получается:
[σ]H=  = 770,9 МПа
= 770,9 МПа
Определяем допускаемое напряжение изгиба
[σ]F=[σ]Flim  (3.2.7)
(3.2.7)
где
[σ]Flim-предел выносливости
SF=1,7- коэффициент запаса прочности
YN=1- коэффициент долговечности, учитывающий влияние ресурса
YR=1- коэффициент, учитывающий влияние шероховатости переходной поверхности между зубьями
YA=1- коэффициент, учитывающий влияние двустороннего приложения нагрузки
подставляя данные в формулу (3.2.7) получается:
[σ]F=  МПа
МПа
3.3 Геометрические параметры тихоходной передачи
Предварительное значение межосевого расстояния, мм
аW=К·(Uт+1)•  (3.3.1)
(3.3.1)
Принимаем К=10
подставляя данные в формулу (3.3.1) получается:
аW=10·(4+1)•  =186,8 мм
=186,8 мм
Ориентировочное значение окружной скорости
V=  (3.3.2)
(3.3.2)
подставляя данные в формулу (3.3.2) получается:
V=  =0,2 м/с
=0,2 м/с
Принимаем степень точности зубчатой передачи 9
Значение межосевого расстояния
аW=Кα·(Uт+1)·  (3.3.3)
(3.3.3)
где:
Uт=4 – передаточное число тихоходной передачи.
Кα=450 Мпа1/3
 Т1 –момент на колесе.
Т1 –момент на колесе.
Ψва=0,4 – коэффициент ширины
[σ]H=770,9•106 Па – расчётное допускаемое контактное напряжение.
КН- коэффициент нагрузки
 (3.3.4)
(3.3.4)
 =1,06- коэффициент, учитывающий внутреннюю динамику нагружения
=1,06- коэффициент, учитывающий внутреннюю динамику нагружения
 =1- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии
=1- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии
 - коэффициент распределения нагрузки между зубьями
- коэффициент распределения нагрузки между зубьями
 (3.3.5)
(3.3.5)
подставляя данные в формулу (3.3.5) получается:

подставляя данные в формулу (3.3.4) получается:

подставляя данные в формулу (3.3.3) получается:
аW=450·(4+1)·  =148,5 мм
=148,5 мм
Принимаем аW=140мм.
Предварительные основные размеры зубчатого колеса
Делительный диаметр колеса
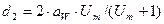 (3.3.6)
(3.3.6)
подставляя данные в формулу (3.3.6) получается:
|
|
|
 мм
мм
Ширина зубчатого колеса
 (3.3.7)
(3.3.7)
подставляя данные в формулу (3.3.7) получается:
 мм
мм
Модуль передачи:
 (3.3.8)
(3.3.8)
Максимально допустимый модуль
 (3.3.9)
(3.3.9)
подставляя данные в формулу (3.3.9) получается:

Минимальное значение модуля
 (3.3.10)
(3.3.10)
Кт=3,4·103
КF=КH=1,31-коэффициент нагрузки
подставляя данные в формулу (3.3.10) получается:

Принимаем mТ=3
Определяем суммарное число зубьев передачи
 (3.3.11)
(3.3.11)
подставляя данные в формулу (3.3.11) получается:


Определяем число зубьев колес и фактическое передаточное число.
Z1= 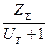 (3.3.12)
(3.3.12)
подставляя данные в формулу (3.3.12) получается:
Z1= 
Принимается Z1=19.
Т.к. Z1>17, то передачу выполняют без смещения.
 (3.3.13)
(3.3.13)
подставляя данные в формулу (3.3.13) получается:

Принимается Z2=74.
Определяем фактическое передаточное число
 (3.3.14)
(3.3.14)
подставляя данные в формулу (3.3.14) получается:

Определяем геометрические параметры колес.
Делительный диаметр шестерни:
 (3.3.15)
(3.3.15)
подставляя данные в формулу (3.3.15) получается:
 мм
мм
Делительный диаметр колеса:
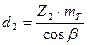 (3.3.16)
(3.3.16)
подставляя данные в формулу (3.3.16) получается:
 мм
мм
Диаметры окружности вершин и впадин зубьев колес:
da1=d1+2·mТ (3.3.17)
df1=d1-2·1,25·mТ
dа2=d2+2·mт
df2=d2-2·1,25·mТ
подставляя данные в формулу (3.3.17) получается:
da1=57+2·3=63 мм
df1=57-2·1,25·3=49,5 мм
dа2=222+2·3=228 мм
df2=222-2·1,25·3=214,5 мм
Ширина зубчатого венца шестерни:
 b1=b2+2·m (3.3.18)
b1=b2+2·m (3.3.18)
подставляя данные в формулу (3.3.18) получается:
b1=56+2·3=62 мм
3.4 Проверка зубьев колес по контактным напряжениям
σН=  [σ]H (3.4.1)
[σ]H (3.4.1)
где:
Zσ=9600 МПа1/2; KH=1,31; T1=834,6 H•м; [σ]H=770,9•106 Па;
b2=56•10-3 м; UТ=3,9; aW=140•10-3 м
подставляя данные в формулу (3.4.1) получается:
σН=  576·106 Па
576·106 Па
576 МПа≤770,9 МПа– условие выполняется
3.5 Силы в зацеплении
Окружная сила в зацеплении:
Ft=  (3.5.2)
(3.5.2)
подставляя данные в формулу (3.5.2) получается:
Ft=  4572,6 H
4572,6 H
Радиальная сила в зацеплении:
Fr=Ft•tgα (3.5.3)
подставляя данные в формулу (3.5.3) получается:
Fr =4572,6·tg20°=1664,3 H
Осевая сила в прямозубом зацеплении равна нулю:
Fa=0 H
3.6 Проверка зубьев колес по напряжениям изгиба
Расчётное напряжение изгиба в зубьях колеса:
 σF2=
σF2=  [σ]F2 (3.6.1)
[σ]F2 (3.6.1)
где KF=1,31
Yε=1-коэффициент, учитывающий перекрытие зубьев
|
|
|
YF2=3,6-коэффициент формы зуба колеса
Yβ=1-коэффициент, учитывающий угол наклона в прямозубой передаче
[σ]F2 =700 МПа
подставляя данные в формулу (3.6.1) получается:
 σF2=
σF2=  МПа<[σ]F
МПа<[σ]F
 Расчётное напряжение изгиба в зубьях шестерни:
Расчётное напряжение изгиба в зубьях шестерни:
 σF1=
σF1=  [σ]F1 (3.6.2)
[σ]F1 (3.6.2)
где
YF1=4,08; YF2=3,6; [σ]F1 =500 МПа
подставляя данные в формулу (3.6.2) получается:
 σF1=
σF1=  МПа<[σ]F
МПа<[σ]F
3.7 Расчет на прочность при действии пиковой нагрузки
σНmax=  [σ]Hmax (3.7.1)
[σ]Hmax (3.7.1)
Где
σH=648 МПа
Кпер=1,8- коэффициент перегрузки
[σ]Hmax =2,8·σТ (3.7.2)
подставляя данные в формулу (3.7.2) получается:
[σ]Hmax =2,8·750=2100 МПа
подставляя данные в формулу (3.7.1) получается:
σНmax=  МПа<[σ]Hmax
МПа<[σ]Hmax
σFmax=  [σ]Fmax (3.7.3)
[σ]Fmax (3.7.3)
Где
σF=145,5 МПа
Кпер=1,8- коэффициент перегрузки
[σ]Fmax =σFlim·YNmax·Kst/Sst (3.7.4)
Где
σFlim=500Мпа- предел выносливости при изгибе
YNmax=4- максимально возможное значение коэффициента долговечно-сти
Kst=1- коэффициент влияния частоты приложения пиковой нагрузки
Sst=2- коэффициент запаса прочности
подставляя данные в формулу (3.7.4) получается:
[σ]Fmax =500·4·1/2=1000 МПа
подставляя данные в формулу (3.7.3) получается:
σFmax=  МПа<[σ]Fmax
МПа<[σ]Fmax
4 Расчёт быстроходной передачи
Из условия соосности аWТ= аWБ=140мм.
4.1 Геометрические параметры быстроходной передачи
Предварительные основные размеры зубчатого колеса
Делительный диаметр колеса
 (4.1.1)
(4.1.1)
 подставляя данные в формулу (4.1.1) получается:
подставляя данные в формулу (4.1.1) получается:
 мм
мм
Ширина зубчатого колеса
 (4.1.2)
(4.1.2)
подставляя данные в формулу (4.1.2) получается:
 мм
мм
Модуль передачи:
 (4.1.3)
(4.1.3)
Максимально допустимый модуль
 (4.1.4)
(4.1.4)
подставляя данные в формулу (4.1.4) получается:

Минимальное значение модуля
 (4.1.5)
(4.1.5)
Кт=3,4·103
КF-коэффициент нагрузки
КF =КH=1,31
подставляя данные в формулу (4.1.5) получается:

Принимаем mб=2
Определяем суммарное число зубьев передачи
 (4.1.6)
(4.1.6)
подставляя данные в формулу (4.1.6) получается:

Определяем число зубьев колес и фактическое передаточное число.
Z3=  (4.1.7)
(4.1.7)
подставляя данные в формулу (4.1.7) получается:
Z3= 
Принимается Z3=26.
Т.к. Z3>17, то передачу выполняют без смещения.
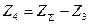 (4.1.8)
(4.1.8)
подставляя данные в формулу (4.1.8) получается:


Принимается Z2=114.
Определяем фактическое передаточное число
 (4.1.9)
(4.1.9)
подставляя данные в формулу (4.1.9) получается:

Определяем геометрические параметры колес.
Делительный диаметр шестерни:
 (4.1.10)
(4.1.10)
подставляя данные в формулу (4.1.10) получается:
 мм
мм
Делительный диаметр колеса:
 (4.1.11)
(4.1.11)
подставляя данные в формулу (4.1.12) получается:
 мм
мм
Диаметры окружности вершин и впадин зубьев колес:
da3=d3+2·mб (4.1.12)
df3=d3-2·1,25·mб
dа4=d4+2·mб
df4=d4-2·1,25·mб
подставляя данные в формулу (4.1.12) получается:
da3=52+2·2=56 мм
|
|
|
df3=52-2·1,25·2=47 мм
dа4=228+2·2=232 мм
df4=228-2·1,25·2=223 мм
Ширина зубчатого венца шестерни:
b3=b4+2·m (4.1.13)
подставляя данные в формулу (4.1.13) получается:
b3=35+2·2=39 мм
4.2 Проверка зубьев колес по контактным напряжениям
σН=  [σ]H (4.2.1)
[σ]H (4.2.1)
где:
Zσ=9600 МПа1/2; KH=1,31; T3=217,2 H•м; [σ]H=770,9•106 Па;
b4=35•10-3 м; Uб=4,4; aW=140•10-3 м
подставляя данные в формулу (4.2.1) получается:
σН=  454·106 Па
454·106 Па
454 МПа≤770,9 МПа– условие выполняется
4.3 Силы в зацеплении
Окружная сила в зацеплении:
Ft=  (4.3.2)
(4.3.2)
подставляя данные в формулу (4.3.2) получается:
 Ft=
Ft=  1976,9 H
1976,9 H
Радиальная сила в зацеплении:
Fr=Ft•tgα (4.3.3)
подставляя данные в формулу (4.3.3) получается:
Fr ==1976,9·tg20°=719,5 H
Осевая сила в прямозубом зацеплении равна нулю:
Fa=0 H
4.4 Проверка зубьев колес по напряжениям изгиба
Расчётное напряжение изгиба в зубьях колеса:
 σF2=
σF2=  [σ]F2 (4.4.1)
[σ]F2 (4.4.1)
где KF=1,31
Yε=1-коэффициент, учитывающий перекрытие зубьев
YF4=3,59-коэффициент формы зуба колеса
Yβ=1-коэффициент, учитывающий угол наклона в прямозубой передаче
[σ]F2 =700 МПа
подставляя данные в формулу (4.4.1) получается:
 σF2=
σF2=  МПа<[σ]F
МПа<[σ]F
Расчётное напряжение изгиба в зубьях шестерни:
 σF1=
σF1=  [σ]F1 (4.4.2)
[σ]F1 (4.4.2)
где
YF3=3,8; YF4=3,59; [σ]F1 =500 МПа
подставляя данные в формулу (4.4.2) получается:
 σF1=
σF1=  МПа<[σ]F
МПа<[σ]F
4.5 Расчет на прочность при действии пиковой нагрузки
σНmax=  [σ]Hmax (4.5.1)
[σ]Hmax (4.5.1)
Где
σH=584 МПа
Кпер=1,8- коэффициент перегрузки
[σ]Hmax =2,8·σТ (4.5.2)
подставляя данные в формулу (4.5.2) получается:
[σ]Hmax =2,8·750=2100 МПа
подставляя данные в формулу (4.5.1) получается:
σНmax=  МПа<[σ]Hmax
МПа<[σ]Hmax
 σFmax=
σFmax=  [σ]Fmax (4.5.3)
[σ]Fmax (4.5.3)
Где
σF=88,5 МПа
Кпер=1,8- коэффициент перегрузки
[σ]Fmax =σFlim·YNmax·Kst/Sst (4.5.4)
Где
σFlim=500Мпа- предел выносливости при изгибе
YNmax=4- максимально возможное значение коэффициента долговечно-сти
Kst=1- коэффициент влияния частоты приложения пиковой нагрузки
Sst=2- коэффициент запаса прочности
подставляя данные в формулу (4.5.4) получается:
[σ]Fmax =500·4·1/2=1000 МПа
подставляя данные в формулу (4.5.3) получается:
σFmax=  МПа<[σ]Fmax
МПа<[σ]Fmax
5 Расчёт валов:
5.1 Предварительный расчёт валов:
 Крутящие моменты в поперечных сечения валов:
Крутящие моменты в поперечных сечения валов:
На тихоходном валу: М3=834,6 Н·м
На промежуточном валу: М2=217,2 Н·м
На быстроходном валу: М1=51,4 Н·м
Входной вал
Диаметр входного конца вала d, мм по расчёту на кручение, при допускаемом напряжении на кручение [τ]=20 МПа определяется по формуле (5.1):
d=  (5.1.1)
(5.1.1)
подставляя данные в формулу (5.1.1) получается:
d=  23,4 мм
23,4 мм
Принимаем d=24 мм
Диаметр мест под подшипники
dП= d+2·tцил (5.1.2)
tцил=3,5 мм- высота заплечика цилиндрического конца вала
подставляя данные в формулу (5.1.2) получается:
dП=24+2·3,5=31,4 мм
Принимаем dП=30 мм
под ведущей шестерней
dБП=dП+3·r (5.1.3)
r=2 мм-фаска подшипника
подставляя данные в формулу (5.1.3) получается:
dБП=30+3·2=36 мм
Принимаем dБП=36мм
Промежуточный вал
При допускаемом напряжении на кручение [τ]=20 МПа диаметр промежуточного вала:
подставляя данные в формулу (5.1.1) получается:
dК=  37,8 мм
37,8 мм
Принимаем dК=38 мм
dБК=dК+3·f (5.1.4)
f=1,2 мм-фаска на ступице колеса
подставляя данные в формулу (5.1.4) получается:
dБК=38+3·1,2=41,6 мм
Принимаем dБК=42 мм
Диаметр мест под подшипники
dП= dК-3·r (5.1.5)
r=2,5 мм-фаска подшипника
подставляя данные в формулу (5.1.5) получается:
 dП= 38-2·2,5=33 мм
dП= 38-2·2,5=33 мм
Принимаем dП=35 мм
dБП=dП+3·r (5.1.6)
r=2,5 мм-фаска подшипника
подставляя данные в формулу (5.1.6) получается:
dБП=35+3·2,5=42,5 мм
Принимаем dБП=42 мм
Выходной вал
При [τ]=20 МПа диаметр выходного вала определяется по формуле:
подставляя данные в формулу (5.1.1) получается:
d=  59,3 мм
59,3 мм
Принимаем d=60 мм.
Диаметр мест под подшипники
dП= d+2·tцил (5.1.7)
tцил=4,6 мм- высота заплечика цилиндрического конца вала
подставляя данные в формулу (5.1.7) получается:
dП=60+2·4,6=69,2 мм
Принимаем dП=70 мм
dБП=dП+3·r (5.1.8)
r=3,5 мм-фаска подшипника
подставляя данные в формулу (5.1.8) получается:
dБП=70+3·3,5=80,5 мм
Принимаем dБП=80 мм
Диаметр мест под колесо
dК=dБП (5.1.9)
подставляя данные в формулу (5.1.9) получается:
dК=80 мм
5.2 Построение эпюр изгибающих и крутящих моментов
 Входной вал
Входной вал
Определение реакций опор


Тогда:

 Н
Н


Тогда:

 Н
Н


Тогда:
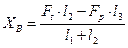
 Н
Н

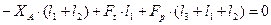
Тогда:

 Н
Н
Построение эпюры МХ
Участок 1 ( )
)

при 

при 
 Н·мм
Н·мм
Участок 2 ( )
)

при 
 Н·мм
Н·мм
при 
 Нмм
Нмм
Построение эпюры МY
Участок 1 ( )
)

при 

при 
 Нмм
Нмм
Участок 2 ( )
)


при 
 Нм
Нм
при 
 Нмм
Нмм
Участок 3 ( )
)

при 
 Нмм
Нмм
при 
 Нмм
Нмм
Построение эпюры суммарного изгибающего момента
Участок 1 ( )
)

при 

при 
 Нмм
Нмм
Участок 2 ( )
)
при 
 Нмм
Нмм
при 
 Нмм
Нмм
Участок 2 ( )
)
при 
 Нмм
Нмм
при 
 Нмм
Нмм
 Промежуточный вал
Промежуточный вал
Определение реакций опор


Тогда:

 Н
Н


Тогда:

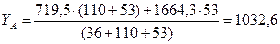 Н
Н


Тогда:

 Н
Н


Тогда:

 Н
Н
Построение эпюры МХ
Участок 1 ( )
)

при 

при 
 Нмм
Нмм
Участок 2 ( )
)

при 
 Нмм
Нмм
при 
 Нмм
Нмм
Участок 3 ( )
)
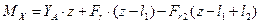
при 
 Нмм
Нмм
при 
 Нмм
Нмм
Построение эпюры МY
Участок 1 ( )
)


при 

при 
 Нмм
Нмм
Участок 2 ( )
)

при 
 Нмм
Нмм
при 
 Нмм
Нмм
Участок 3 ( )
)

при 
 Нмм
Нмм
при 
 Нмм
Нмм
Построение эпюры суммарного изгибающего момента
Участок 1 ( )
)

при 

при 
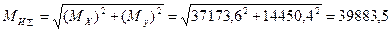 Нмм
Нмм
Участок 2 ( )
)
при 
 Нмм
Нмм
при 
 Нмм
Нмм
Участок 2 ( )
)
при 
 Нмм
Нмм
при 

Выходной вал
Определение реакций опор
 Н
Н


Тогда:

 Н
Н



Тогда:

 Н
Н


Тогда:

 Н
Н


Тогда:

 Н
Н
Построение эпюры МХ
Участок 1 ( )
)

при 

при 
 Нмм
Нмм
Участок 2 ( )
)

при 
 Нмм
Нмм
при 
 Нмм
Нмм
Построение эпюры МY


