Построение фигуры пересечения многогранника плоскостью

Построение изображений

Свои исходные данные, взятые из приложения по своему варианту, записываются в форме таблицы

Точка	Координата	Точка	Координата
x	y	z	x	y	z
G
K				M
L				N
G’				R

 

Стоим проекции вершины G по координатам (таблица) в натуральном масштабе: по координате x=60 мм, по координате y=32 мм, по координате z=6 мм.

Аналогично строим проекции вершин K (K₁, K₂, K₃) и L (L₁, L₂, L₃) нижнее основание и вершины G (G₁, G₂, G₃) верхнего основания призмы. Строим проекции ребер основания GKL и бокового ребра GG’ тонкими линиями.

Затем строим проекции определителя плоскости и оформляем его сторонами ∆ MNR. Стороны треугольника секущей плоскости удобно начертить штриховой линией, чтобы после окончательного определения видимости объектов обвести основной линией только его видимую часть.

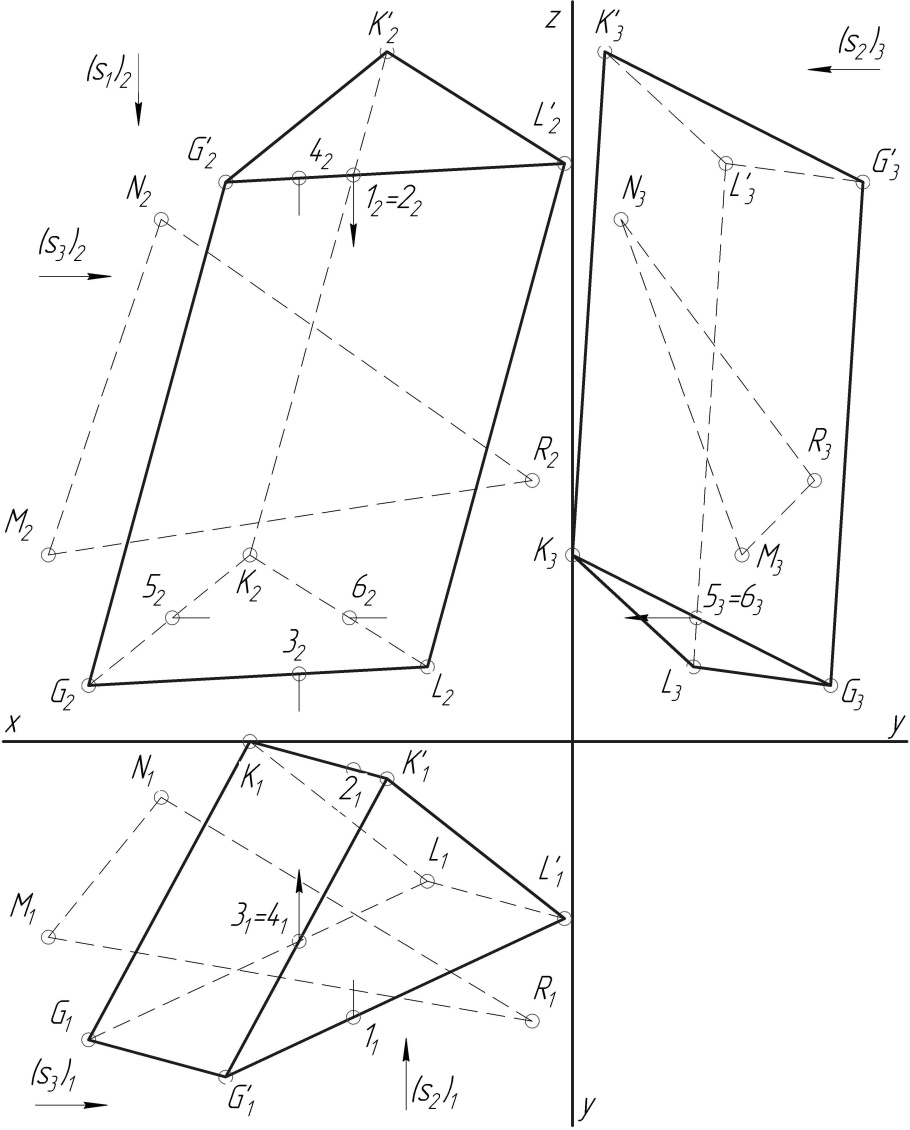По свойству призмы и проекций параллельных прямых (соответствующие ребра равны и параллельны) достраиваем проекции боковых ребер и второе основание многогранника. Для определения видимости граней используем конкурирующие точки. Например, горизонтальные проекции G₁L₁ и G’₁K’₁ ребер оснований пересекаются, а в пространстве они пересечься не могут, следовательно, точки 3₁ ϵ G₁L₁ и 4₁ ϵ G’₁K’₁ являются проекциями горизонтально конкурирующих точек 3 и 4. По линии связи отмечаем их фронтальные проекции 3₂ и 4₂ на соответствующих проекциях ребер оснований. Направление (s₁)₂ проецирования для горизонтальной плоскости проекции соответствует направлению нашего взгляда на объект. У точки 4₂ высота больше, следовательно, она находится ближе к наблюдателю, поэтому видна и закрывает собой точку 3. Вывод: на горизонтальной проекции точка 3 не видна, следовательно, не видна проекция G₁L₁ ребра основания, не видна проекция вершины L₁ и ребер K₁L₁, L₁L’₁, следовательно, не видны и грани, в состав которых входят эти рёбра.

Для определения видимости на фронтальной проекции призмы используем фронтально конкурирующие точки 1 (1₂ → 1₁) и 2 (2₂ → 2₁). По их горизонтальной проекции и направлению проецирования (взгляда) (s₂)₁ делаем вывод, что точка 1 находится перед точкой 2 и поэтому видна её проекция 1₂. Следовательно, проекция отрезка K₂K’₂ ребра KK’ не видимая, поэтому не видимые и соответствующие грани. На профильной проекции конкурируют точки 5 и 6. По положению фронтальных проекций 5₂ и 6₂ этих точек и направлению проецирования (s₃)₂ делаем вывод, что на профильной проекции видимой является точка 5 (5₃) и ребро KG (K₃G₃). Отсюда делаем вывод, что проекция L₃L’₃ бокового ребра и соответствующие грани призмы не видны.

Построение фигуры пересечения многогранника плоскостью

Построение линии сечения призмы состоит из последовательного решения задач пересечения прямых линий (рёбер) с заданной плоскостью или пересечения двух плоскостей: грани многогранника и заданной плоскости.

Рассмотрим построение фигуры сечения трехгранной призмы, которую мы построили, способом пересечения прямой (ребра) с плоскостью.

Вначале вспомним алгоритм решения задачи пересечения прямой линии с плоскостью.

Дано: d – прямая линия (возьмём ребро KK’), α (MNR) – секущая плоскость

Найти: точку B=d∩α

Решение: 1) d δ(δ₂) – строим фронтально проецирующую плоскость, проходящую через прямую d (в примере её проекция δ₂ совпадает с проекцией K₂K’₂ ребра). Для этого на направлении линии K₂K’₂ чертим утолщенную линию длиной около 8 мм и ставим обозначение δ₂.

2) Строим прямую линию (7-8) = δ∩α. На чертеже отмечаем точки 7₂ = N₂R₂ ∩ K₂K’₂ → 7₁; 8₂ = M₂R₂ ∩ K₂K’₂ → 8₁ и строим горизонтальную проекцию (7₁ – 8₁) прямой пересечения вспомогательной плоскости с заданной.

3) B = d∩(7 – 8) – пересечение прямой (7 – 8) с ребром KK’ определяет положение точки B: B₁=(7₁-8₁)∩K₁K’₁ → B₂ K₂K’₂.

Это основной прием решения задачи

Заключаем ребро GG’ во формально проецирующую плоскость β (β₂ = G₂G’₂ – по направлению G₂G’₂ чертим утолщенную линию и обозначение β₂). Так как β║δ, то линии их пересечения с плоскостью α (MNR), будут параллельны. Поэтому строим: 9₂ → 9₁ N₁R₁; через точку 9₁ проводим прямую линию параллельно линии (7₁ – 8₁) и отмечаем точку 11₁ на продолжении проекции G’₁G₁ – это горизонтальная проекция точки пересечения GG’ с плоскостью α.

Прямая (B₁ – 11₁) является горизонтальной проекцией линии пересечения грани GG’K’K с плоскостью α. Точка 11₁ находится за пределами проекции G’₁G₁ действительного ребра G’G, следовательно, линия сечения ограничится точкой A (A₁) пересечения ребра GK (G₁K₁) основания с плоскостью α. По линии связи отмечаем проекцию A₂ и строим прямую B₂A₂ штриховой линией, потому что она не видимая т.к. принадлежит невидимой грани. А её горизонтальная проекция видна потому, что на горизонтальной проекции данная грань видимая.

Аналогично, вводим плоскость γ (γ₂) LL’ (γ₂=L₂L’₂) и строим: 10₂→10₁ ϵ прямая 2 (7₁ – 8₁) → С₁ ϵ L₁L’₁ → C₂ ϵ L₂L’₂ → строим (C₁ – 11₁) → D₁ = (C₁ – 11₁) ∩ G₁L₁ → D₂.

Построенные проекции точек пересечения рёбер призмы с плоскостью α сечения соединяем прямыми линиями с учетом их видимости и получаем две проекции (A₁B₁C₁D₁, A₂B₂C₂D₂) фигуры сечения ABCD.

Профильную проекцию A₃B₃C₃D₃ строим из условия принадлежности точек фигуры сечения соответствующим рёбрам.

Относительную видимость призмы и материальной треугольной пластины определяем по конкурирующим точкам или просто по элементарной логике. Заметим, что фигура сечения принадлежит плоскости треугольника MNR. На горизонтальной проекции сторона A₁B₁ видимая, следовательно, видимым является и участок линий M₁R₁ и N₁R₁, пересекающихся с ней со стороны видимой грани, т.е. видимой является левый участок нашего треугольника. На линии AB (A₁B₁) он пересёк грань GG’K’K, затем происходит внутри призмы, на линии CD (С₁D₁) треугольник вышел из призмы на невидимой грани, следовательно, он продолжает оставаться невидимым до тех пор, пока его изображение перекрывается изображением призмы.

Аналогично, на фронтальной проекции треугольник виден на участке его вершины R (R₂), где он пересек призму по видимой линии CD (С₂D₂). На профильной проекции, по тем признакам, видимым является часть треугольника со стороной NM (N₃M₃).

Там, где изображение видимой части пластины треугольника накладывается на изображение призмы, участки призмы не видимы и её рёбра должны изображаться штриховой линией. Видимые линии сторон треугольной пластины и каркаса призмы обводим основными линиями.

Построение фигуры пересечения многогранника плоскостью (Рисунок)

 

 

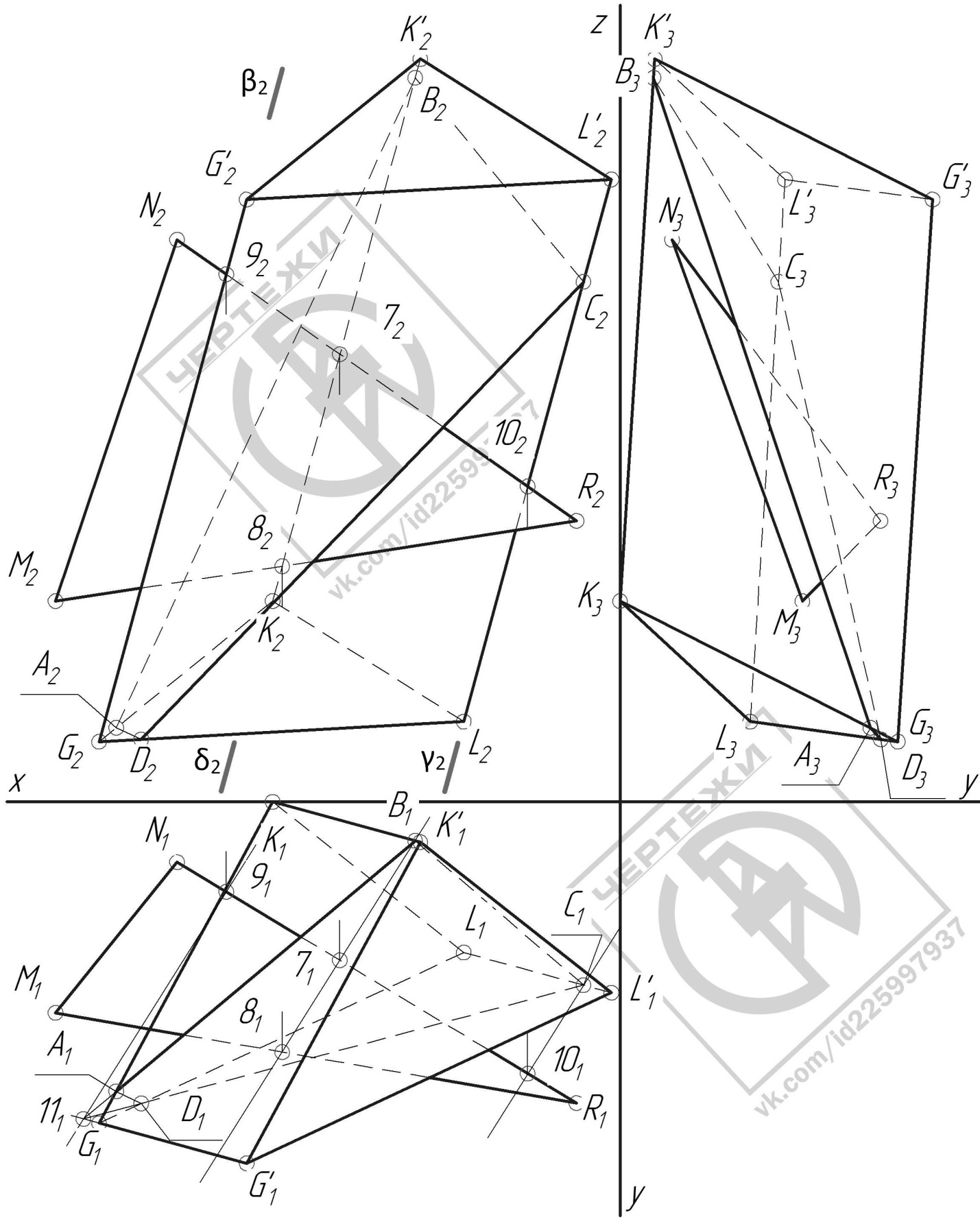
Поделиться:

Воспользуйтесь поиском по сайту: