Проблема соотношения выборки и генеральной совокупности

Проблемы применения математической статистики для решения интересующих нас задач начинаются с обоснования возможности использования выборочных частот в качестве хороших оценок генеральных вероятностей. Некоторые обстоятельства заставляют настороженно относиться к этому. Рассмотрим эти обстоятельства подробнее.

1) На практике нередко нарушаются условия вероятностного порождения данных.

вероятность какого-либо события – это некая числовая характеристика степени возможности его появления в определенных, могущих повторяться неограниченное число раз, условиях. Определили мы и круг рассматриваемых событий – они состоят в том, что те или иные признаки принимают те или иные значения. В социологии само определение вероятности в некоторых ситуациях может стать бессмысленным в силу ряда причин. Как правило, бывает неясно, каков тот комплекс условий, повторение которого требуется для соответствующего осмысления. Даже если некоторое смутное понимание сути этого комплекса условий у исследователя имеется, чаще всего отсутствует уверенность в том, что этот комплекс в принципе может быть повторен и что даже при допущении его повторения мы будем иметь постоянную долю случаев реализации нашего события. В таких случаях теряет смысл гипотеза о вероятностном порождении исходных данных, принятие которой является необходимым условием корректности использования методов математической статистики.

Для оправдания вероятностного подхода к пониманию социологических закономерностей заметим, что упомянутая "повторяемость" предстает перед социологом в виде появления сходных ситуаций, разнесенных либо в пространстве, либо во времени. Такая точка зрения, как известно, использовалась, например, Контом, выдвинувшим в качестве основных исследовательских методов для социологии т.н. экспериментальный и сравнительный методы (в первом под экспериментом понимается исследование изменений в состоянии общества, возникающих под воздействием тех или иных потрясений, во втором – имеется в виду сравнение жизни людей, живущих в разных частях земного шара) [Конт, 1996].

Однако если в какой-то ситуации некое событие произошло, а в другой – нет, то мы практически никогда не узнаем ответа на вопрос: является ли это проявлением того, что вероятность этого события меньше единицы (реализовав много ситуаций и подсчитав долю тех, в которых наше событие свершилось, мы тем самым получим оценку соответствующей вероятности), либо же следствием того, что разные ситуации отвечают разным комплексам условий, задающих вероятность, и что поэтому вероятности нашего события в этих ситуациях различны.

Подобные рассуждения справедливы отнюдь не только для социологии. Л огика развития многих наук, имеющих дело со статистическими данными, привела к необходимости "узаконивания" методов, либо не опирающихся на допущения о вероятностной природе исходных данных и, как следствие, не дающих возможности переносить результаты с выборки на генеральную совокупность), либо предполагающих подобную модель, но такую, адекватность которой невозможно проверить.

Для того чтобы как-то отделить ис пользование математико-статистических методов в описанных ситуациях (являющееся некорректным) от их классического воплощения, для обозначения интересующих нас псевдостатистических подходов и был предложен термин "анализ данных". Это – первая причинапоявления этого термина.

2) Отнюдь не всегда бывает ясно, какова изучаемая генеральная совокупность.

Социолог имеет в своем распоряжении всего одну выборку, при том такую, принципы соотнесения которой с генеральной совокупностью часто бывают неясными. Более того, социолог далеко не всегда уверен в том, что исследуемое им множество объектов вообще является выборкой из какой бы то ни было генеральной совокупности. Вообще, вопрос о том, что есть генеральная совокупность, по отношению к которой изучаемые объекты составляют выборку, в социологии является зачастую весьма непростым. Позволим здесь привести цитату из работы [Божков, 1988, с. 135-136], где говорится, что теоретическое обоснование и выявление качественного состава генеральной совокупности является "отнюдь не формальным и не тривиальным.... Даже в рамках одного исследования бывают альтернативные (и множественные) решения этого вопроса. Более того, проблема определения генеральной совокупности может стать задачей или даже целью исследования. Иначе говоря, это проблема методологического, а вовсе не методико-математического характера." Мы полностью разделяем это мнение. Методы поиска закономерностей "в среднем" в подобной ситуации нельзя отнести к области математической статистики, даже если внешне они схожи с известными математико-статистическими алгоритмами. Использование этих методов в указанной ситуации было отнесено к области анализа данных. Это – вторая причинапоявления этого термина.

Таким образом, указанные сложности в применении методов математической статистики для нужд социолога в каком-то смысле преодолимы. Ниже будем полагать, что некая гипотетическая генеральная совокупность существует (хотя мы, может быть, и не знаем, какова она), и что имеющиеся в нашем распоряжении выборочные частоты – это хорошие оценки соответствующих генеральных вероятностей. Другими словами, будем считать, что вычисленное для выборки частотное распределение хорошо отражает отвечающую нашему признаку (группе признаков) случайную величину, сочтем возможным работать с этим распределением так, как правила математической статистики предписывают работать с распределением вероятностей.

Однако использование классических математико-статистических приемов соответствующего рода, зачастую, оказывается невозможным еще по нескольким причинам, также часто возникающим не только в социологии, но и в других науках, опирающихся на анализ эмпирических данных.

3) Д ля многих методов отсутствуют разработанные способ ы перенесения результатов их применения с выборки на генеральную совокупность.

Методы переноса результатов с выборки на генеральную совокупность обычно базируются на довольно серьезных теоретических результатах. Соответствующая теория не разработана для очень многих методов, интересующих социолога (например, для многих методов классификации). В результате научная ценность получаемых с их помощью выводов оказывается весьма сомнительной: их нельзя распространить ни на какую совокупность, кроме той, для которой они были получены. Из такого положения имеется два выхода.

Во-первых, можно положиться на интуицию исследователя и считать, что результаты справедливы для некой интуитивным образом понимаемой генеральной совокупности. Так чаще всего и поступают.

Во-вторых, приложив определенные усилия, связанные с активным использованием ЭВМ, требующиеся оценки можно получить эмпирическим путем. Дело в том, что, как мы уже упоминали, правила интересующего нас переноса опираются на изучение распределений определенных статистик. Эти распределения можно искусственно создавать, рассчитывать требующиеся статистики и эмпирическим путем изучать их распределения. Другими словами, с помощью такого подхода математическая статистика из теоретической науки превращается в экспериментальную. Такой подход активно развивается на Западе, где получил название Boot s trap [Ермаков, Михайлов, 1982; Эфрон, 1988]. В последние годы он довольно часто используется и в отечественной науке.

Приведем цитату из работы [Ростовцев и др.,1997, с. 174-175]: "Классические методы статистики развивались, когда вычислительная техника еще не имела достаточного быстродействия, поэтому исследуемые статистики подбирались так, чтобы была возможность оценить их распределения.... Современные средства анализа позволяют существенно расширить множество статистик и упростить расчеты. В частности, для оценки значимости нередко нет необходимости проводить сложные теоретические исследования распределений статистик, достаточно иметь мощный компьютер и воспользоваться методом Монте-Карло либо провести прямые вычисления вероятностей [Ермаков, Михайлов, 1982]".

4) Перенос результатов с выборки на генеральную совокупность может быть затруднен из-за осуществления "ремонта" выборки (например, ее перевзвешивания), что нередко делает социолог. Тут тоже может помочь моделирование случайных данных на ЭВМ.

Методы, для которых отсутствует строгий механизм переноса результатов с выборки на генеральную совокупность, тоже были отнесены к области анализа данных. Это – третья причина возникновения этого термина.

 

13. Стандартное отклонение, характеризует среднее отклонение от среднего значения выборки. Среди этих двух величин(дисп. И ст.откл.) наиболее важное значение имеет стандартное отклонение. Это значение можно представить как среднее расстояние, на котором находятся элементы от среднего элемента выборки. Дисперсию трудно интерпретировать содержательно. Однако,квадратный корень из этого значения является стандартным отклонением и хорошо поддается интерпретации. Стандартное отклонение вычисляется путем определения сначала дисперсии и затем вычисления квадратного корня из дисперсии. Стандартное отклонение показывает, насколько хорошо среднее значение описывает всю выборку. Среднее квадратическое отклонение (о) представляет собой корень квадратный из дисперсии: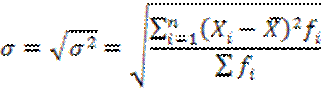

Среднее квадратическое отклонение показывает, насколько е среднем колеблется величина признака у единиц исследуемой совокупности, и выражается в тех же единицах измерения, что и варианты.

Коэффициент вариации - наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Он измеряет среднеквадратическое отклонение в % от среднего. Со­вокупность считается однородной, если коэффициент вариации не превышает 33 % для распределений, близких к нормальному. Коэффициент вариации применяется для сравнения колеблемости разнородных признаков. Коэффициент вариации часто используется для сравнения размеров вариации в совокупностях, отличающихся друг от друга величиной средней (в совокупностях с разными уровнями):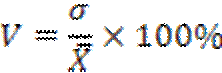

Оценка степени интенсивности вариации возможна только для каждого отдельного признака и совокупности определенного состава. При этом при равенстве коэффициентов вариации для раз­личных признаков или в разных совокупностях вариация в одних случаях может считаться как сильная, а в других - как слабая. Различная сила, интенсивность вариации обусловлены объективны­ми причинами.

 

 

11. сре́днее арифмети́ческое — одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений, деленную на их количество.Средняя арифметическая применяется, когда объем совокупности представляет собой сумму всех индивидуальных значений варьирующего признака. Следует отметить, что если вид средней величины не указывается, подразумевается средняя арифметическая.

Расчет средней арифметической в рядах распределения: Если значения осредняемого признака заданы в виде интер­валов ("от — до"), т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве зна­чений признаков в группах принимают середины этих интерва­лов, в результате

чего образуется дискретный ряд.

Свойства средней арифмет-ой:

1) Если все индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в i раз, то среднее значение нового признака соответственно уменьшится или увеличится в i раз.

2). Если все варианты осредняемого признака уменьшить или уве­личить на число А, то средняя арифметическая соответст­венно уменьшится или увеличится на это же число А.

3) сумма отклонений отдельных значений признака от ср.арифм. равна нулю

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: