 |
Поляризация при отражении и преломлении
|
|
|
|
Закон Брюстера
Пусть угол падения i таков, что отраженный луч перпендикулярен преломленному, т.е. r = π/2 - iБр. Это условие называют условием Брюстера (см. рисунок ниже), а угол - углом Брюстера - iБр.
 Используя закон преломления
Используя закон преломления 
получим формулу, определяющую угол Брюстера:
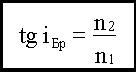 При выполнении условия Брюстера i + r = π/2, тогда из формулы Френеля для получим:
При выполнении условия Брюстера i + r = π/2, тогда из формулы Френеля для получим: 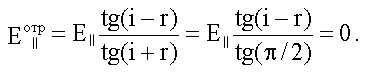
Таким образом, при выполнении условия Брюстера, отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения.
Это утверждение носит название закона Брюстера.
Закон Брюстера имеет простое объяснение. Отраженная световая волна появляется за счет излучения электронов среды, совершающих вынужденные колебания под действием вектора преломленной волны. Это излучение имеет направленный характер: его интенсивность равна нулю в направлении колебаний зарядов. Направим под углом Брюстера на границу раздела плоско поляризованную волну с вектором, лежащим в плоскости падения.
32.
(33) Явление полного внутреннего отражения. При падении света на границу двух диэлектриков, для которых  (рис.4.12), из закона Снеллиуса следует, что существует предельный (или критический) угол п. падения, при котором угол преломления
(рис.4.12), из закона Снеллиуса следует, что существует предельный (или критический) угол п. падения, при котором угол преломления  . Тогда
. Тогда
 .(4.85)При
.(4.85)При  угол преломления 2 имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными.
угол преломления 2 имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными.
Когда угол падения 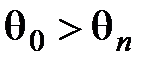 , не существует вещественного угла преломления 2, т.к. закон Снеллиуса дает для sin2 значение больше единицы, а для cos2 – чисто мнимое значение:
, не существует вещественного угла преломления 2, т.к. закон Снеллиуса дает для sin2 значение больше единицы, а для cos2 – чисто мнимое значение:
 (4.86)
(4.86)
Но формулы Френеля останутся справедливыми и в этом случае, если закон преломления рассматривать просто как определение входящих в них величин sin2 и cos2 в соответствии с (4.86). Справедливость понимаемых таким образом формул Френеля следует из того, что они обеспечивают выполнение граничных условий и в этом случае.
|
|
|
Рассмотрим сначала световую волну во второй среде (преломленную) в общем случае:
 (4.87)
(4.87)
В такой записи сомножитель I означает комплексную амплитуду волны II, распространяющейся вдоль оси X со скоростью  . Подставим (4.86) в (4.87):
. Подставим (4.86) в (4.87):
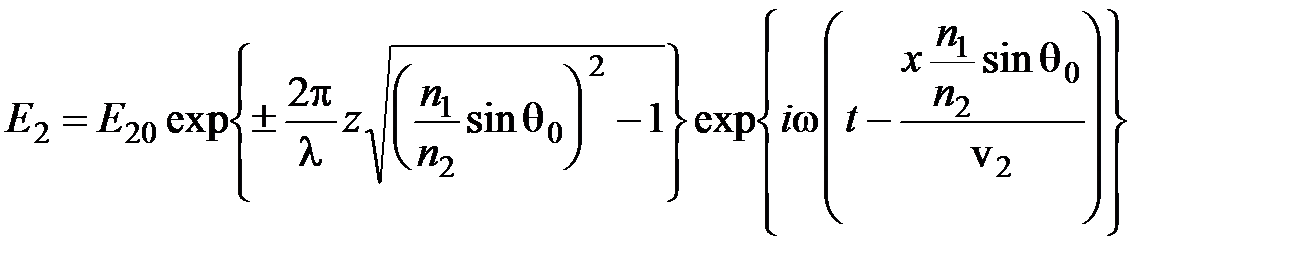 . (4.88)
. (4.88)
 Знак (+) в первой экспоненте соответствует безграничному возрастанию поля в среде, что лишено физического смысла. Поэтому остается (–), что соответствует быстро убывающей с ростом z амплитуде волны, распространяющейся во второй среде вдоль X. Практически эта неоднородная волна существует лишь в поверхностном слое второй среды толщиной порядка длины волны. Причем фазовая скорость этой неоднородной (и соответственно не плоской) зависит как от свойств среды, так и от угла падения.
Знак (+) в первой экспоненте соответствует безграничному возрастанию поля в среде, что лишено физического смысла. Поэтому остается (–), что соответствует быстро убывающей с ростом z амплитуде волны, распространяющейся во второй среде вдоль X. Практически эта неоднородная волна существует лишь в поверхностном слое второй среды толщиной порядка длины волны. Причем фазовая скорость этой неоднородной (и соответственно не плоской) зависит как от свойств среды, так и от угла падения.
Формулы Френеля для отраженной волны ((4.56) и (4.67) с учетом (4.86)) имеют вид:
 ; (4.89)
; (4.89)
 . (4.90)
. (4.90)
 Видно, что энергетические коэффициенты
Видно, что энергетические коэффициенты  при углах падения больше критического (рис.4.13). Поэтому это явление называется полным внутренним отражением(ПВО). При этом волна и соответствующая доля энергии проникают через границу раздела во вторую среду на некоторую глубину d (глубину проникновения) (амплитуда поля на глубине d падает в е раз): (4.91)
при углах падения больше критического (рис.4.13). Поэтому это явление называется полным внутренним отражением(ПВО). При этом волна и соответствующая доля энергии проникают через границу раздела во вторую среду на некоторую глубину d (глубину проникновения) (амплитуда поля на глубине d падает в е раз): (4.91)
движутся вдоль поверхности раздела и затем возвращаются в первую среду. Места входа энергии во вторую среду и ее возвращения в первую смещены друг относительно друга. Амплитуды p– и s– компонент отраженной волны не изменяются по абсолютному значению, но испытывают различные фазовые сдвиги. Если представить, что
 (4.92)
(4.92)
то
 (4.93)
(4.93)
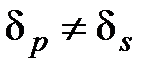 .Обозначим
.Обозначим  (4.94)
(4.94)
Тогда  . (4.95)
. (4.95)
Примеры:1. Призма–крыша. 2.Световоды. 3.Миражи.
4.Ромб (параллелепипед) Френеля ( ).
).
(34.) Поглощение света.Закон Бугера.
Поглощение света в веществе связано с преобразованием энергии электромагнитного поля волны в тепловую энергию вещества (или в энергию вторичного фотолюминесцентного излучения). Закон поглощения света (закон Бугера) имеет вид:
|
|
|
I=I0 exp(-ax), (1)
где I0, I -интенсивности света на входе (х=0) и выходе из слоя среды толщины х, a-коэффициент поглощения, он зависит от l.
Для диэлектриков a=10-1¸ 10-5 м-1, для металлов a=105¸ 107 м-1, поэтому металлы непрозрачны для света.
Зависимостью a (l) объясняется окрашенность поглощающих тел. Например, стекло, слабо поглощающее красный свет, при освещении белым светом будет казаться красным.
(35.)Диспе́рсия све́та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты).
Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является неодинаковая скорость распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно чем больше частота волны, тем больше показатель преломления среды и меньше ее скорость света в ней:
у красного цвета максимальная скорость в среде и минимальная степень преломления,
у фиолетового цвета минимальная скорость света в среде и максимальная степень преломления. По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только к электромагнитной волне, но к любому волновому процессу.
Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая).
Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем, в том числе фотографических и видео-объективов.
|
|
|
Коши пришел к формуле, выражающей зависимость показателя преломления от длины волны:
n = a + b / L2 + c / L4 + …,
где:
L — длина волны в вакууме;
a, b, c, … — постоянные, значения которых для каждого вещества должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши.
Дисперсионные призмы, призмы для пространственного разделения излучений различных длин волн; применяются главным образом в спектральных приборах. Разделение излучений в Д. п. является результатом зависимости угла отклонения d луча, прошедшего через призму (см. рис.), от показателя преломления n, различного для лучей разных длин волн
(36.) Фазовой скоростью v монохроматичной волны принято называть скорость распространения волнового фронта. В среде с показателем преломления n фазовая скорость υ равна (6.1)
 Здесь
Здесь  – круговая частота, k – волновое число, c – скорость света в вакууме. Как показывает опыт, все без исключения среды обладают дисперсионными свойствами – волны разных частот распространяются в средах с различными фазовыми скоростями. Это явление называют дисперсией. Закон дисперсии можно задать либо в виде зависимости показателя преломления от частоты
– круговая частота, k – волновое число, c – скорость света в вакууме. Как показывает опыт, все без исключения среды обладают дисперсионными свойствами – волны разных частот распространяются в средах с различными фазовыми скоростями. Это явление называют дисперсией. Закон дисперсии можно задать либо в виде зависимости показателя преломления от частоты  , либо в виде функции
, либо в виде функции  , либо, наконец, в виде зависимости волнового числа от частоты
, либо, наконец, в виде зависимости волнового числа от частоты  . В качестве аргумента в законе дисперсии может быть вместо
. В качестве аргумента в законе дисперсии может быть вместо  использована длина волны
использована длина волны  в среде.
в среде.
Обычно в теории рассматривается так называемая групповая скорост ь, то есть скорость перемещения центра волновой группы или точки с максимальным значением амплитуды (точка B). Рассмотрим простой случай – распространение амплитудно-модулированной волны. При z = 0, то есть на входе в диспергирующую среду, колебание можно записать в виде 
Этот процесс может быть представлен в виде суперпозиции трех синусоидальных колебаний с частотами  ,
,  ,:
,:  (6.3) Каждая из этих спектральных компонент будет распространяться в среде со своей фазовой скоростью:
(6.3) Каждая из этих спектральных компонент будет распространяться в среде со своей фазовой скоростью:  Таким образом при z > 0 можно записать:
Таким образом при z > 0 можно записать:  Рассмотрим случай достаточно малых значений z, удовлетворяющих условию
Рассмотрим случай достаточно малых значений z, удовлетворяющих условию 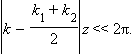 В этом случае высокочастотные колебания частоты, описываемые 1-ым и 2-ым слагаемыми в (6.5), практически не отличаются по фазе и могут быть объединены. Тогда
В этом случае высокочастотные колебания частоты, описываемые 1-ым и 2-ым слагаемыми в (6.5), практически не отличаются по фазе и могут быть объединены. Тогда  Функцию E(z, t) можно рассматривать как амплитудно-модулированную волну с медленно изменяющейся во времени и пространстве амплитудой
Функцию E(z, t) можно рассматривать как амплитудно-модулированную волну с медленно изменяющейся во времени и пространстве амплитудой  Как видно из (6.7) модулируемая волна распространяется с фазовой скоростью
Как видно из (6.7) модулируемая волна распространяется с фазовой скоростью  . Скорость распространения огибающей, то есть модулирующей волны, есть
. Скорость распространения огибающей, то есть модулирующей волны, есть  Это и есть групповая скорость.
Это и есть групповая скорость.
|
|
|
37.
(38.) Описание анизотропных сред. Оптической анизотропией называется зависимость оптических свойств среды от направления распространения света в ней. Физическая природа анизотропии вещества связана с особенностями строения его молекул или особенностями кристаллической решетки, в узлах которой находятся атомы или ионы. Взаимодействие света с веществом для анизотропных сред не может быть моделировано колебаниями одного осциллятора. Для описания таких сред необходимо ввести три различных взаимно перпендикулярных осциллятора и характеризовать три взаимно перпендикулярных направления различными значениями показателя преломления. В анизотропной среде проекции поляризованности связаны с проекциями напряженности электрического поля соотношениями:  (9.1)
(9.1)
В дальнейшем для простоты будем нумеровать декартовы оси координати соответствующие им проекции числами или индексами 1, 2, 3. Матрица величин ij называется тензором диэлектрической восприимчивости. Тогда систему (9.1) можно записать в компактном виде:  (9.2)
(9.2)
Соотношение между компонентами вектора электрического смещения D и поляризованностью P для анизотропной среды принимает вид:
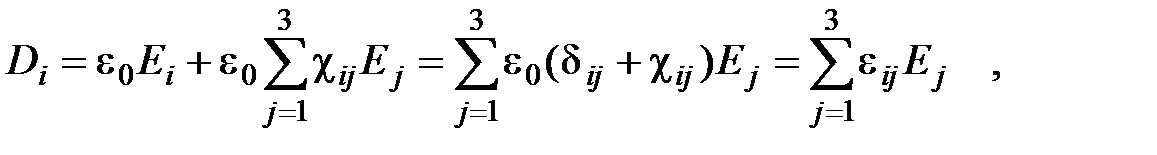 (9.3)
(9.3)
где ij – символ Кронекера. Тензор ij:
 (9.4)
(9.4)
называется тензором диэлектрической проницаемости.
Двулучепреломление. Плоскость, проходящая через луч, направленный под углом к оптической оси и оптическую ось, называется главной. Из этого определения и определения главной оси следует, что у луча, вектор E 0 которого направлен перпендикулярно главной плоскости, скорость не зависит от направления и равна лучевой скорости, направленной коллинеарно оптической оси. Такой луч называется обыкновенным. Соответствующие ему параметры (скорость, показатель преломления) обозначаются индексом «о». У луча, вектор E е которого лежит в главной плоскости, скорость зависит от направления, т.к. соответствующая полуось эллипса в сечении эллипсоида изменяется с изменением направления луча. Такой луч называется необыкновенным.
39.
(40.) Эллиптическая и круговая поляризацияПусть вдоль оси x распространяются две плоскополяризованные когерентные световые волны, у которых колебания вектора  происходят вдоль осей y и z, соответственно (см. рисунок ниже).
происходят вдоль осей y и z, соответственно (см. рисунок ниже).
|
|
|


Так как колебания векторов  и
и  когерентны, то при их сложении получится вектор
когерентны, то при их сложении получится вектор  , конец которого будет, в общем случае, описывать эллипс в плоскости y, z. Такой свет называют эллиптически поляризованным. Ориентировка эллипса и направление вращения конца вектора
, конец которого будет, в общем случае, описывать эллипс в плоскости y, z. Такой свет называют эллиптически поляризованным. Ориентировка эллипса и направление вращения конца вектора  зависит от разности фаз α При α = 0, α = ±π эллипс вырождается в прямую: результирующая волна будет плоскополяризована. При α = ±π/2 и
зависит от разности фаз α При α = 0, α = ±π эллипс вырождается в прямую: результирующая волна будет плоскополяризована. При α = ±π/2 и  конец вектора
конец вектора  будет двигаться по кругу. В этом случае говорят, что свет поляризован по кругу.
будет двигаться по кругу. В этом случае говорят, что свет поляризован по кругу.
41.
(42.) Тепловое излучение. В нагретых телах часть внутренней энергии вещества может превращаться в энергию излучения. Поэтому нагретые тела являются источниками электромагнитного излучения в широком диапазоне частот. Это излучение называют тепловым излучением.
Эксперименты показывают, что тепловое излучение имеет непрерывный спектр. Это означает, что нагретое тело испускает некоторое количество энергии излучения в любом диапазоне частот или длин волн. Распределение энергии излучения тела по спектру зависит от температуры тела. При этом для всех тел с увеличением температуры максимум энергии излучения смещается в коротковолновый участок спектра, а общая энергия излучения возрастает.
Характеристики теплового излучения. Для описания спектрального состава теплового излучения рассмотрим энергию, излучаемую единицей поверхности нагретого тела в единицу времени в узком диапазоне частот от  до
до  . Этот поток лучистой энергии
. Этот поток лучистой энергии  , испускаемый с единицы поверхности тела по всем направлениям, пропорционален ширине спектрального диапазона, то есть
, испускаемый с единицы поверхности тела по всем направлениям, пропорционален ширине спектрального диапазона, то есть  . Энергию
. Энергию  , приходящуюся на единичный диапазон частот, называют спектральной испускательной способностью тела или спектральной плотностью энергетической светимости. Опыт показывает, что для каждого тела испускательная способность является определенной функцией частоты, вид которой изменяется при изменении температуры тела
, приходящуюся на единичный диапазон частот, называют спектральной испускательной способностью тела или спектральной плотностью энергетической светимости. Опыт показывает, что для каждого тела испускательная способность является определенной функцией частоты, вид которой изменяется при изменении температуры тела  . В дальнейшем для такой функциональной зависимости
. В дальнейшем для такой функциональной зависимости  , рассматриваемой при заданном значении температуры тела как некоторая функция частоты, будем использовать принятое в теории теплового излучения обозначение:
, рассматриваемой при заданном значении температуры тела как некоторая функция частоты, будем использовать принятое в теории теплового излучения обозначение:  .
.
(43.) Закон Кирхгофа. Между испускательными и поглощательными свойствами любого тела должна существовать связь. Ведь в опыте с равновесным тепловым излучением (рис. 1.1) равновесие в системе может установиться только в том случае, если каждое тело будет излучать в единицу времени столько же энергии, сколько оно поглощает. Это означает, что тела, интенсивнее поглощающие излучение какой-либо частоты, будут это излучение интенсивнее и испускать.
Поэтому, в соответствии с таким принципом детального равновесия, отношение испускательной и поглощательной способностей одинаково для всех тел в природе, включая абсолютно черное тело, и при данной температуре является одной и той же универсальной функцией частоты (длины волны).
Этот закон теплового излучения, установленный в 1859 г. Г.Кирхгофом при рассмотрении термодинамических закономерностей равновесных систем с излучением, можно записать в виде соотношения  или
или 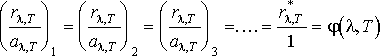 где индексы 1, 2, 3... соответствуют различным реальным телам.
где индексы 1, 2, 3... соответствуют различным реальным телам.
Абсолютно чёрное тело — физическая идеализация, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой.
(44.)Первый закон излучения Вина  где:
где:
 — плотность энергии излучения
— плотность энергии излучения
 — частота излучения
— частота излучения
 — температура излучающего тела
— температура излучающего тела
 — функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений.
— функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений.
Первая формула Вина справедлива для всех частот. Любая более конкретная формула (например, закон Планка) должна удовлетворять первой формуле Вина.
Из первой формулы Вина можно вывести закон смещения Вина (закон максимума) и закон Стефана — Больцмана, но нельзя найти значения постоянных, входящих в эти законы.
Закон смещения Вина
Длина волны, при которой энергия излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина: 
где T — температура в кельвинах, а λmax — длина волны с максимальной интенсивностью в метрах.
Так, если считать в первом приближении, что кожа человека близка по свойствам к абсолютно чёрному телу, то максимум спектра излучения при температуре 36 °C (309 К) лежит на длине волны 9400 нм (в инфракрасной области спектра).
Видимый цвет абсолютно чёрных тел с разной температурой представлен на диаграмме.
Закон Стефана — Больцмана Мощность излучения абсолютно чёрного тела (интегральная мощность по всему спектру), приходящаяся на единицу площади поверхности, прямо пропорциональна четвёртой степени температуры тела:
 ,где j — мощность на единицу площади излучающей поверхности, а
,где j — мощность на единицу площади излучающей поверхности, а 
Вт/(м²·К4) — постоянная Стефана — Больцмана.
Таким образом, абсолютно чёрное тело при T = 100 K излучает 5,67 ватт с квадратного метра своей поверхности. При температуре 1000 К мощность излучения увеличивается до 56,7 киловатт с квадратного метра.
Для нечёрных тел можно приближённо записать: 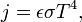
где ε — степень черноты (для всех веществ ε < 1, для абсолютно чёрного тела ε = 1).
(45.)Закон Рэлея — Джинса
закон Рэлея — Джинса
Попытка описать излучение абсолютно чёрного тела исходя из классических принципов термодинамики и электродинамики приводит к закону Рэлея — Джинса:
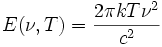
Эта формула предполагает квадратичное возрастание спектральной плотности излучения в зависимости от его частоты. На практике такой закон означал бы невозможность термодинамического равновесия между веществом и излучением, поскольку согласно ему вся тепловая энергия должна была бы перейти в энергию излучения коротковолновой области спектра. Такое гипотетическое явление было названо ультрафиолетовой катастрофой.
Тем не менее закон излучения Рэлея — Джинса справедлив для длинноволновой области спектра и адекватно описывает характер излучения. Объяснить факт такого соответствия можно лишь при использовании квантово-механического подхода, согласно которому излучение происходит дискретно. Исходя из квантовых законов можно получить формулу Планка, которая будет совпадать с формулой Рэлея — Джинса при  .
.
Закон Планка
Формула Планка
Зависимость мощности излучения чёрного тела от длины волны
Интенсивность излучения абсолютно чёрного тела в зависимости от температуры и частоты определяется законом Планка:

где I(ν)dν — мощность излучения на единицу площади излучающей поверхности в диапазоне частот от ν до ν + dν.
Эквивалентно,
 ,
,
где u(λ)dλ — мощность излучения на единицу площади излучающей поверхности в диапазоне длин волн от λ до λ + dλ.
(46.) под действием света происходит вырывание электронов из вещества катода – фотоэлектрический эффект (внешний) (или просто – фотоэффект).
Законы фотоэффекта.
1.При неизменном спектральном составе света сила фототока насыщения прямо пропорциональна падающему на катод световому потоку.
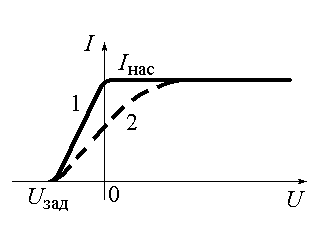 2.Начальная кинетическая энергия вырванных светом электронов линейно растет с ростом частоты света и не зависит от его интенсивности.
2.Начальная кинетическая энергия вырванных светом электронов линейно растет с ростом частоты света и не зависит от его интенсивности.
3.Фотоэффект не возникает, если частота света меньше некоторой характерной для каждого металла величины к, называемой красной границей фотоэффекта.
Как уже отмечалось, Эйнштейн в 1905 г., развивая квантовую теорию Планка, выдвинул идею, излучение, поглощение и распространение света происходит порциями (квантами), энергия которых равна  . В этом случае можно записать закон сохранения энергии для элементарного процесса, заключающегося во взаимодействии одного кванта с веществом, сводящегося к передаче электрону дискретного количества энергии. При этом нужно учесть, что электрон в металле не является свободным и, чтобы покинуть металл, электрон должен преодолеть работу выхода A. Применяя к фотоэффекту в металлах закон сохранения энергии, Эйнштейн предложил следующую формулу:
. В этом случае можно записать закон сохранения энергии для элементарного процесса, заключающегося во взаимодействии одного кванта с веществом, сводящегося к передаче электрону дискретного количества энергии. При этом нужно учесть, что электрон в металле не является свободным и, чтобы покинуть металл, электрон должен преодолеть работу выхода A. Применяя к фотоэффекту в металлах закон сохранения энергии, Эйнштейн предложил следующую формулу:  ,
,
где A – работа выхода электрона из металла, v – скорость фотоэлектрона. При этом считается, что каждый квант выбивает только один электрон (однофотонный процесс).
Как следует из (11.1), фотоэффект в металлах может возникать только при  , в противном случае энергии кванта недостаточно для вырывания электрона из металла. Отсюда можно найти минимальную частоту света, при которой происходит фотоэффект (красную границу фотоэффекта):
, в противном случае энергии кванта недостаточно для вырывания электрона из металла. Отсюда можно найти минимальную частоту света, при которой происходит фотоэффект (красную границу фотоэффекта): 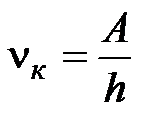 .
.
(Пусть между анодом и катодом (рис.11.1) приложен тормозящий потенциал (U < 0) (рис.11.2). Если кинетическая энергия электронов достаточна, то они, преодолев тормозящее поле, все таки создают фототок. В фототоке участвуют те электроны, для которых удовлетворяется условие  . Величина задерживающего потенциала U зад определяется из условия:
. Величина задерживающего потенциала U зад определяется из условия:  , (11.4)
, (11.4)
где vmax – максимальная скорость выбитых электронов. Подставив (11.4) в (11.1), получаем:  , откуда
, откуда  .Т.о., величина задерживающего потенциала не зависит от интенсивности, а зависит только от частоты падающего света, что и объясняет второй закон фотоэффекта. В отличие от металлов в полупроводниках и диэлектриках также возникает так называемый внутренний фотоэффект, состоящий в возбуждении электронов из валентной зоны в зону проводимости.
.Т.о., величина задерживающего потенциала не зависит от интенсивности, а зависит только от частоты падающего света, что и объясняет второй закон фотоэффекта. В отличие от металлов в полупроводниках и диэлектриках также возникает так называемый внутренний фотоэффект, состоящий в возбуждении электронов из валентной зоны в зону проводимости.
(47.) Давление света

В 1873 г. Дж. Максвелл, исходя из представлений об электромагнитной природе света, пришел к выводу: свет должен оказывать давление на препятствие (благодаря действию силы Лоренца; на рисунке v - направление скорости электронов под действием электрической составляющей электромагнитной волны).
Квантовая теория света объясняет световое давление как результат передачи фотонами своего импульса атомам или молекулам вещества. Пусть на поверхность абсолютно черного тела площадью S перпендикулярно к ней ежесекундно падает N фотонов:  . Каждый фотон обладает импульсом
. Каждый фотон обладает импульсом 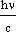 . Полный импульс, получаемый поверхностью тела, равен
. Полный импульс, получаемый поверхностью тела, равен  . Световое давление:
. Световое давление: 
При падении света на зеркальную поверхность удар фотона считают абсолютно упругим, поэтому изменение импульса и давление в 2 раза больше, чем при падении на черную поверхность (удар неупругий).
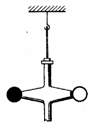
Это давление оказалось ~4.10-6 Па. Предсказание Дж. Максвеллом существования светового давления было экспериментально подтверждено П. Н. Лебедевым, который в 1900 г. измерил давление света на твердые тела, используя чувствительные крутильные весы. Теория и эксперимент совпали.
Опыты П. Н. Лебедева — экспериментальное доказательство факта: фотоны обладают импульсом
(48.) Эффект Комптона (Комптон-эффект) — явление изменения длины волны электромагнитного излучения вследствие рассеивания его электронами. Обнаружен американским физиком Артуром Комптоном в 1923 году для рентгеновского излучения. В 1927 Комптон получил за это открытие Нобелевскую премию по физике.  Иллюстрация к эффекту КомптонаПри рассеянии фотона на покоящемся электроне частоты фотона
Иллюстрация к эффекту КомптонаПри рассеянии фотона на покоящемся электроне частоты фотона 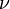 и
и  (до и после рассеяния соответственно) связаны соотношением:
(до и после рассеяния соответственно) связаны соотношением:  где
где  — угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).Перейдя к длинам волн:
— угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).Перейдя к длинам волн:  где
где  — комптоновская длина волны электрона.Для электрона
— комптоновская длина волны электрона.Для электрона 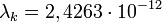 м. Уменьшение энергии фотона после комптоновского рассеяния называется комптоновским сдвигом. В классической электродинамике рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не сопровождается уменьшением её частоты.Объяснить эффект Комптона в рамках классической электродинамики невозможно. С точки зрения классической физики электромагнитная волна является непрерывным объектом и в результате рассеяния на свободных электронах изменять свою длину волны не должна. Эффект Комптона является прямым доказательством квантования электромагнитной волны, другими словами подтверждает существование фотонов. Эффект Комптона является ещё одним доказательством справедливости корпускулярно-волнового дуализма микрочастиц.
м. Уменьшение энергии фотона после комптоновского рассеяния называется комптоновским сдвигом. В классической электродинамике рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не сопровождается уменьшением её частоты.Объяснить эффект Комптона в рамках классической электродинамики невозможно. С точки зрения классической физики электромагнитная волна является непрерывным объектом и в результате рассеяния на свободных электронах изменять свою длину волны не должна. Эффект Комптона является прямым доказательством квантования электромагнитной волны, другими словами подтверждает существование фотонов. Эффект Комптона является ещё одним доказательством справедливости корпускулярно-волнового дуализма микрочастиц.
49.
50.
|
|
|


