 |
Формы записи линеаризованных уравнений
|
|
|
|
В теории управления принято записывать дифференциальные уравнения в двух стандартных формах.
В общем виде линеаризованное дифференциальное уравнение, описывающее элемент, можно записать следующим образом
(2.7)
где y(t), x(t), f(t) - выходная и входная величины элемента и внешнее воздействие;
ai, bi, ci - постоянные коэффициенты;
n - порядок уравнения, причем (n³m,k); это условие физической реализуемости элемента, показывающее, что сигнал на выходе реального элемента не может возникнуть раньше подачи воздействия на его вход, т.е.
y(t) = 0 при t < 0,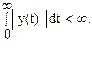 
Уравнение (2.7) удобнее записывать в символическом виде, введя алгебраизированный символ дифференцирования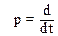 
. В результате уравнение примет вид
(a0pn + a1pn -1 +…+an-1p+an) y(t) =
= (b0pm +b1pm-1 +…+bm) x(t) + (c0pk +c1pk-1 +…+ck) f(t). (2.8)
Коэффициенты уравнения имеют размерности:
ai [cn-i]; bi 
; ci 
.
В общем случае в соответствии с (2.8) уравнение элемента можно представить в форме
D(p) y(t) = N(p) x(t) + M(p) f(t). (2.9)
При этом
; 
; 
-
полиномы степени n, m, k от символа дифференцирования p.
Первая стандартная форма записи. Дифференциальное уравнение записывают так, чтобы выходная величина и ее производные находились в левой части уравнения, а входные величины и все остальные члены - в правой. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Чтобы привести уравнение (2.8) к такому виду, разделим левую и правую его части на an и получим
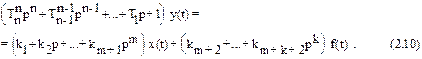
При записи уравнения в первой стандартной форме (2.10) получившиеся коэффициенты:
Тn, Тn-1,…, Т1 называются постоянными времени, они имеют размерность времени [с] и характеризуют инерционные свойства элемента; а
k1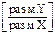 
, …, km+1 
, km+2 
, …, km+k+2 
называются коэффициентами передачи. Они представляют собой весовые коэффициенты, показывающие какой вклад в формирование выходной величины элемента вносит каждое слагаемое правой части уравнения.
|
|
|
Вторая стандартная форма записи. Для решения дифференциальных уравнений широкое распространение получил операторный метод, при использовании которого задача нахождения решения дифференциального уравнения сводится к алгебраическим действиям. Чтобы перейти от исходного дифференциального уравнения элемента при нулевых начальных условиях к операторному, необходимо в дифференциальном уравнении вместо реальных функций времени записать их изображения по Лапласу, а в полиномах символ дифференцирования p заменить на оператор Лапласа s.
Применив к дифференциальному уравнению (2.9) преобразование Лапласа, получим
D(s)Y(s) = N(s) X(s) + M(s) F(s), (2.11)
где s – оператор Лапласа;
Y(s), X(s), F(s) - изображения по Лапласу выходной и входной величин элемента и внешнего воздействия;
; 
; 
полиномы степени n, m, k от оператора Лапласа s.
Оператор Лапласа s представляет собой комплексную величину, причем s=c+jw, где:
c=Re s - абсцисса абсолютной сходимости;
w=Im s –угловая частота, имеющая размерность [рад/с];
Для перехода от реальных функций времени - оригиналов к их изображениям по Лапласу и наоборот введены прямое и обратное интегральные преобразования вида:
,
.
На практике для этих целей используют специальные таблицы [1,7].
Уравнения (2.9) и (2.11) формально совпадают между собой. Однако уравнение (2.9) является дифференциальным, куда входят реальные функции времени, а уравнение (2.11) - алгебраическим относительно изображений функций времени по Лапласу.
После ввода следующих обозначений:
; 
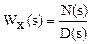уравнение (2.11) примет вид, являющийся второй стандартной формой записи
Y(s) = Wx(s) X(s) + Wf(s) F(s). (2.12)
Выражения Wx(s) и Wf(s) в теории управления называются передаточными функциями.
Если f(t) = 0, то F(s) = 0 и тогда 
- передаточная функция элемента по входу Х.
|
|
|
Eсли x(t)=0, то X(s)=0 и тогда 
- передаточная функция элемента по входу F.
Передаточная функция элемента по заданному входу есть отношение изображений по Лапласу его выходной и входной величин при нулевых начальных условиях и равных нулю воздействиях на остальных входах элемента.
Передаточная функция имеет важное основополагающее значение в классической теории управления. Она устанавливает связь в динамическом режиме между выходной и входной величинами элемента и полностью характеризует его динамические свойства.
Понятие передаточной функции весьма удобно при анализе так называемых структурных схем. Так, например, элемент, изображенный на рис. 2.2, после линеаризации можно представить в виде структурной схемы, показанной на рис. 2.3.
Рис. 2.3. Структурная схема элемента
Передаточные функции элементов или отдельных участков схемы позволяют легко получить общее уравнение всей системы, а в случае необходимости перейти к дифференциальному уравнению.
Замечание: в литературе часто оператор Лапласа обозначается буквой p.
ВОПРОСЫ К РАЗДЕЛУ 2
1. Каково назначение математического описания систем?
2. Что такое динамика системы? Чем отличается математическое описание динамики системы от описания ее статики?
3. Что представляет собой условие физической реализуемости системы?
4. В чем смысл линеаризации нелинейных элементов?
5. Каким образом линеаризуются дифференциальные уравнения?
6. Назовите формы записи линеаризованных уравнений.
7. Каким образом перейти к первой форме записи дифференциального уравнения звена? Как в этом случае называются коэффициенты?
8. Как перейти от дифференциального уравнения к операторному?
9. Дайте определение передаточной функции.
10.Как по дифференциальному уравнению звена найти его передаточную функцию?
Содержание Глоссарий
|
|
|
