 |
Биномиальное распределение
|
|
|
|
СТАТИСТИЧЕСКИЙ КОНТРОЛЬ И УПРАВЛЕНИЕ ПРОЦЕССАМИ В СИСТЕМАХ КАЧЕСТВА
(законы распределения вероятностей)
Основы теории и практики
Учебное пособие
Набережные Челны – 2001
Введение
В данном пособии мы рассмотрим три важнейших статистических закона распределения, которые обеспечивают математическое обоснование вопросов, связанных с качеством. Эти законы - биномиальный, Пуассона и нормальный закон распределения. Они значимы в том случае, когда оценивается вероятность или значимость конкретного числа выявленных бракованных изделий, дефектов и измеренных значений.
Рассмотрим также вопросы, связанные с погрешностью или изменчивостью, возникающими при производстве продукции или оказании услуги.
По способу отбора изделий, подвергаемых контролю качества различают сплошной (стопроцентный) и выборочный контроль. В крупносерийном и массовом производстве контроль подвергают только часть партии – выборку (n). В том случае, если уровень качества изделия в выборке соответствует установленным требованиям, то партию можно принять как годную, в противном случае партия бракуется.
В различных случаях получают разные законы распределения вероятностей попадания годных и дефектных изделий в выборку. Вследствие этого необходимо правильно выбирать математический аппарат для оценки качества контроля.
При выборочном контроле в основном применяют биномиальный, Пуассона и нормальный законы распределения. Первые два являются законами распределения случайных величин, когда испытания серий имеют только два исхода («годное» или «дефектное»). Нормальный закон используется при контроле по количественным признакам.
|
|
|
Параметры распределения вероятности и выборки
Данные параметры разделяют на характеристики расположения и рассеяния.
Основной характеристикой расположения является среднее значение, которое определяется как среднее арифметическое (
) и находится по формуле:
,
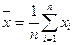где n – число наблюдений;
х – текущее значение данного наблюдения.
Основной мерой рассеяния выборочных значений является дисперсия (s2), характеризующая степень разброса количественных измерений индивидуальных значений выборки относительно среднего значения для этой выборки. Дисперсия определяется по одной из двух следующих формул:
Вторая из них используется для достаточно больших n (n>10).
Среднее квадратичное отклонение (s) определяется по формулам:
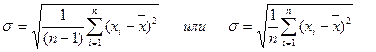
Математическое ожидание (m) представляет собой наиболее вероятное ожидаемое значение этой величины. Математическое ожидание дискретной случайной величины равно сумме произведений всех возможных ее значений (х) на их вероятности (р):
Размах – величина, равная разнице между наибольшим и наименьшим значением выборки х1….хn:
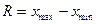
Биномиальное распределение
Если партия из большого числа изделий N содержит некоторую долю дефектных изделий р, некоторую долю годных изделий q, то вероятность получения дефектного изделия в отдельном испытании составит р, а вероятность годного изделия будет равна q = 1-р.
При применении выборочного метода контроля вероятность того, что в выборке объема n число дефектных изделий в точности равно х (х=x1+x2+…+xn) определяется по формуле:
,
где p – вероятность появления брака,
q – вероятность появления годного изделия,
- число возможных групп по х элементов в каждой, которые можно составить из n различных элементов, пренебрегая порядком элементов в каждой группе.
При использовании биномиального закона на практике определяют кумулятивную вероятность, т.е. накопленную вероятность F(n, x). Данная величина оценивает накопление дефектных изделий в выборке и находится по формуле:
|
|
|
где k – число дефектных изделий, для которых выполняется расчет.
Биномиальный закон применяют для: - определения выборки, позволяющей осуществить приемку по альтернативным признакам (число бракованных изделий); - управления процессом «р» (процент брака).
|
|
|
