Обратное преобразование Лапласа

Обратным преобразованием Лапласа функции комплексного переменного , называется функция вещественной переменной, такая что:

где — некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича.

При нулевых на­чальных условиях наличие индуктивности равносильно разрыву цепи, а ёмкости – короткому замыканию:

Если начальные условия ненулевые, то индуктивный элемент в момент коммутации играет роль идеального источника тока, а емкостной - идеального источника ЭДС.

2. Прямое и обратное преобразование Фурье. Связь изображений по Лапласу с изображениями по Фурье.

Преобразование Фурье

 

Соотношение

называют прямым преобразованием Фурье. Функция угловой частоты – называется Фурье-изображением или частотным спектром функции . Спектр характеризует соотношение амплитуд и фаз бесконечного множества бесконечно малых синусоидальных компонент, составляющих в сумме непериодический сигнал . Операция преобразования Фурье математически записывается следующим образом:

где - символ прямого преобразования Фурье.

Спектры в теории автоматического управления представляют графически, изображая отдельно их действительную и мнимую части:

На рис. 1 представлено типичное изображение спектра непериодического сигнала.

Рис. 1

Отметим следующие особенности спектра непериодической функции :

1. Спектр непериодической функции времени непрерывен;

2. Область допустимых значений аргумента спектра

Действительная часть спектра – четная функция частоты, мнимая часть спектра – нечетная функция, что позволяет использовать одну половину спектра

Преобразование Фурье обратимо, то есть, зная Фурье-изображение, можно определить исходную функцию – оригинал. Соотношение обратного преобразования Фурье имеет следующий вид:

Или в сокращенной записи , где - символ обратного преобразования Фурье. Заметим, что временная функция имеет преобразование Фурье тогда и только тогда, когда:

· функция однозначна, содержит конечное число максимумов, минимумов и разрывов;

· функция абсолютно интегрируема, то есть

Обратное преобразование Фурье возможно только в том случае, если все полюсы - левые.

Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом :

Примечание: в этих выражениях опущен масштабирующий множитель , который часто включается в определения преобразования Фурье.

Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.

3. Вывод системы дифференциальных уравнений (СДУ), описывающих
динамику нагруженного LCR-ФНЧ 2 порядка.

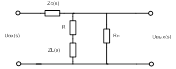
На первом этапе необходимо составить систему дифференциальных уравнений, описывающих состояние ФНЧ. На вход ФНЧ подаётся гармони­ческий сигнал. Будем использовать следующие обозначения переменных:

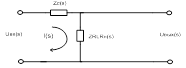
4. Вывод СДУ, описывающих динамику нагруженного LCR-ФВЧ 2 порядка.

Дифференциальное уравнение, описывающее динамику процессов в ФВЧ 2-го порядка, по второму закону Кирхгофа

Дифференциальное уравнение для цепи по первому закону Кирх­гофа

Учитывая, что данная СДУ запишется в виде

5. Вывод выражений для АЧХ, ФЧХ и ЛАЧХ нагруженного LCR-ФНЧ 2 порядка.

6. Вывод выражений для АЧХ, ФЧХ и ЛАЧХ нагруженного LCR-ФВЧ 2 порядка.

 

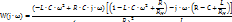
7. Составление нелинейных уравнений для поиска f и f _пп по АЧХ для нагруженного LCR-ФНЧ 2 порядка. (ответ 5 вопроса)

 

8. Составление нелинейных уравнений для поиска f и f _пп по АЧХ для нагруженного LCR-ФВЧ 2 порядка. (ответ 6 вопроса)

9. Составление нелинейных уравнений для поиска f и f _пп по ЛАЧХ для нагруженного LCR-ФНЧ 2 порядка. (ответ 5 вопроса) L(w)=20*log(A(w))

10. Составление нелинейных уравнение для поиска f₀ и f_ПП по ЛАЧХ для нагруженного LCR-ФВЧ 2 порядка.

Рис.10.1. ЛАЧХ для LCR-ФВЧ 2 порядка.

Для нагруженного режима, при 1000R резонансная частота не имеет значение.

Рис.10.2. Производный от функции L3() фильтра LCR-ФВЧ для нагруженного режима.

12 .Блок-схема алгоритма метода дихотомии для решения нелинейных уравнений.

13. Блок-схема алгоритма метода касательных (метода Ньютона) для решения нелинейных уравнений.

14. Блок-схема алгоритма метода секущих для решения нелинейных уравнений.

 

15. Интерполяция функции каноническими полиномами

16. Интерполяция функции полиномами Лагранжа

17. Интерполяция функции полиномами Ньютона

 

 

18. Интерполяция функции кубическими сплайнами

19. Метод Эйлера для решения дифференциальных уравнений

20, 21. Метод Рунге-Кутта второго порядка с полным шагом для решения дифференциальных уравнений

22. Метод Рунге-Кутта второго порядка с половинным шагом для решения дифференциальных уравнений

 

23. Метод Рунге-Кутта четвёртого порядка для решения дифференциальных уравнений

24. Дискретное преобразование Фурье

Существуют два способа представления сигнала - один из них основан на математическом представлении сигнала как функции времени x=f(t), где независимая переменная t - время, и второй в виде X=F(w), где независимая переменная w - частота. При преобразовании Фурье происходит преобразование из одной формы представления сигнала в другую. Если сигнал имеет аналоговый вид - представляет собой непрерывную функцию, определенную на бесконечном промежутке времени, то преобразование Фурье производится по известным формулам. (Первая формула для прямого преобразования Фурье, вторая - для обратного):

 

 

Для дискретного сигнала представляющего собой решетчатую функцию и, как правило, определенного на конечном промежутке времени (времени измерения) преобразование Фурье принимает вид так называемого дискретного преобразования Фурье (ДПФ):

 

 

где: T - период дискретизации

n - номер отсчета дискретизированного сигнала, n=0,1,2,:, N-1;

k - номер гармоники сигнала, k=0,1,2,:, N-1, частота гармоник равна k/T_изм, где T_изм- период измерения;

W - вспомогательная функция.

Недостатком данного алгоритма является большой объем повторяющихся вычислений W^nkпри различных комбинациях n и k. Устранение этих избыточных операций приводит к так называемому алгоритму быстрого преобразования Фурье, который обычно и используется.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: