 |
Синтез моделей как инструмент повышения точности прогнозирования
|
|
|
|
Математическое моделирование как метод исследования и прогнозирования развития различных объектов народного хозяйства и формирования значений отдельных параметров объектов по праву приобретает широкое распространение у специалистов аналитических служб различных компаний. Очевидно, что один и тот же объект подвергается моделированию различными группами исследователей, каждая из которых строит модели, используя различные методики, а, главное, исходя из собственных представлений о поведении объекта. Это обстоятельство приводит к появлению некоторого количества моделей одного и того же объекта, которые отличаются наборами факторов, объясняющих поведение моделируемой величины, разнообразием математических функций, лежащих в их основе и несовпадением результатов.
Учитывая, что каждая из моделей построена корректно и адекватно описывает поведение объекта, встает вопрос: как использовать полученные разными авторами модели для получения наилучшего прогноза моделируемой переменной. Другими словами, ставится задача построения такой математической процедуры, которая бы, используя различные модели, давала бы наиболее точный (с минимальной ошибкой) прогноз относительно каждой из моделей. Задача не выбрать наилучшую модель из числа имеющихся, а построить наилучшую оценку с учетом «мнения» всех моделей.
Математически поставленную задачу можно сформулировать следующим образом.
Пусть имеются m моделей прогнозирования эндогенной переменной P, каждая из которых доставляет некоторую оценку величины P. Обозначим эти оценки символами P (1), P (2), …, P ( m ) и составим из них вектор
Рт={ P (1), P (2), …, P ( m ) }. (1)
|
|
|
Задача заключается в вычислении комбинации  величин (1), такой, которая оказалась бы ближе к искомой величине Р, чем каждая из оценок (1) в отдельности. Точная постановка этой задачи требует следующих предположений. Во-первых, предполагаем, что каждая оценка P ( i ) из набора (1) имеет структуру
величин (1), такой, которая оказалась бы ближе к искомой величине Р, чем каждая из оценок (1) в отдельности. Точная постановка этой задачи требует следующих предположений. Во-первых, предполагаем, что каждая оценка P ( i ) из набора (1) имеет структуру
P ( i ) = Р + u ( i ),(2)
где u ( i ) - случайная ошибка оценки P ( i ). Во-вторых, постулируем, что ошибка u ( i ) обладает нулевым математическим ожиданием и некоторой дисперсией:
Е (u(i)) = 0 (3)
σ i 2 = Var(u(i)) (4)
Методику проверки предположения (3) рассмотрим ниже, а сейчас отметим, что систему равенств (2) можно с учётом (1) - (4) интерпретировать как систему уравнений наблюдений величины Р (схема Гаусса - Маркова). Добавим, что в ситуации (5) мерой близости оценки P ( i ) к искомой величине Р служит среднее квадратическое отклонение σ i, причем равенства (3) - (4) равносильны равенствам:
Е (P(i)) = P; σ 2 (P(i)) = σ i 2 (5)
Комбинацию  величин (1) определим так, чтобы одновременно оказались справедливыми два требования:
величин (1) определим так, чтобы одновременно оказались справедливыми два требования:
E (  ) = P (6)
) = P (6)
σ 2 (  ) => min (7)
) => min (7)
Это и будет означать более высокую точность величины  по сравнению с каждой оценкой P ( i ) в отдельности. Комбинацию
по сравнению с каждой оценкой P ( i ) в отдельности. Комбинацию  разыщем в классе однородных линейных функций аргументов (1):
разыщем в классе однородных линейных функций аргументов (1):
 = c 1 P (1) + c 2 P (2),+ …+ cmP ( m ) (8)
= c 1 P (1) + c 2 P (2),+ …+ cmP ( m ) (8)
где числа c 1, c 2,…, cm подлежат определению согласно требованиям (6) и (7). Образуем из этих констант вектор
C т ={ c 1, c 2,…, cm } (9)
Пусть известна ковариационная матрица S вектора оценок (1) и эта матрица невырождена, т.е.:
│ S │≠ 0 (10)
Методику оценивания элементов матрицы S рассмотрим ниже. Добавим, что матрицу S всегда можно представить в виде:
S = σ 0 2 Q (11)
где σ02 - произвольная положительная константа. Диагональные элементы матрицы Q ={ qii } имеют смысл обратных весов оценок P ( i ) из набора (1):
qii = σ i 2 / σ 0 2 (12)
причём, чем больше qii, тем грубее оценка P ( i ).
|
|
|
С учетом предпосылок (1) - (2) комбинация (8) будет обладать свойством несмещенности (6), если коэффициенты (9) данной комбинации удовлетворяет равенству:
Σ с i = 1тС=1 (13)
где 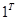 = {1, 1,…, 1} - строка из единиц. Далее, с учетом (11), дисперсия комбинации (8) определяется по правилу:
= {1, 1,…, 1} - строка из единиц. Далее, с учетом (11), дисперсия комбинации (8) определяется по правилу:
σ 2 (  ) = C т SC = σ 0 2 C т QC (15)
) = C т SC = σ 0 2 C т QC (15)
Значит, искомые коэффициенты (9) оптимальной комбинации (8) являются решением классической задачи математического программирования:
C т QC => min (16)
1тС = 1
Решение задачи (16) методом неопределенных множителей Лагранжа с функцией Лагранжа
L (C, λ) = C т · Q · C + λ ·(1-1тС) (17)
имеет вид:
С = Q -1 1 /1T. Q. 1 (18)
В выражении (18) величина
1т Q -1 1 = W (19)
является суммой всех элементов матрицы Q -1. Подставляя правую часть равенства (18) в (8), находятся искомую оптимальную комбинацию величины (8)
 = CT * P = (1 T Q -1)/ W * P (20)
= CT * P = (1 T Q -1)/ W * P (20)
и ее дисперсию:
σ 2 (  ) = σ 0 2 / W (21)
) = σ 0 2 / W (21)
Замечание. Оптимальная комбинация (20) является частным случаем процедуры обобщенного метода наименьших квадратов Эйткена. Подчеркнем, что при массовых расчетах по алгоритму (20) удобно сначала подготовить вектор (19), а затем уже вести вычисления по формуле (8).
Точность оценки  целесообразно с учетом (21) рассчитывать так:
целесообразно с учетом (21) рассчитывать так:
σ(  ) =σ 0 /
) =σ 0 /  (22)
(22)
σ 0 2 = (UTQ -1 U)/(m -1) (23)
где U ={ u 1, u 2,…, um } - вектор оценок случайных ошибок в уравнениях наблюдений (2).
|
|
|


