Раздел 2_1. Функции, их свойства и графики

1. Числовая функция, способы задания, область определения, множество значений. Основные свойства функции: монотонность, ограниченность, периодичность, четность – нечетность. Понятие об обратной функции. Приращение аргумента и приращение функции.
2. Графики функций. Простейшие преобразования графиков функций..
3. Понятие предела функции в точке и на бесконечности. Основные теоремы о пределах. Первый замечательный предел. Техника вычисления пределов функций.
4. Числовая последовательность и ее предел. Монотонность, ограниченность, сходимость числовой последовательности. Второй замечательный предел, число e. Непрерывность функции в точке и на отрезке. Свойства непрерывных на отрезке функций.
5. Функции, пределы, непрерывность в примерах и задачах. Зачетное занятие по теме.

В результате изучения темы студенты должны знать:

§ Определения числовой функции, способы задания;

§ Общие свойства функций: монотонность, ограниченность, периодичность, четность – нечетность;

§ Методику простейших преобразований графиков функций;

§ Определения предела функции в точке и на бесконечности, определение предела числовой последовательности;

§ Свойства функций, непрерывных на отрезке;

§ Первый и второй замечательные пределы.

В результате изучения темы студенты должны уметь:

§ Строить графики элементарных функций, изученных в школе;

§ Находить область определения и множество значений несложных функций;

§ Находить приращение функции в указанной точке и в общем виде;

§ Проводить простейшие преобразования графиков функций;

§ Вычислять пределы функций в точке и на бесконечности;

§ Вычислять пределы числовых последовательностей;

§ Применять замечательные пределы к вычислению пределов различных функций;

§ Применять теорию пределов к решению задач и выводов формул;

 

Занятие 2.1.1. Числовая функция: основные понятия и определения.

1)Числовая функция, способы задания.

2)Область определения, множество значений, методика их нахождения.

3)Основные свойства функции: монотонность, ограниченность, периодичность, четность – нечетность.

4)Понятие об обратной функции, условия и техника отыскания обратной функции

5)Приращение аргумента и приращение функции:

6)Нахождение приращения функции в указанной точке и в общем виде.

 

       Мы приступаем к изучению очередной темы колледжной математики первого курса.

Знаете, что математика делится условно на элементарную и высшую. Ядром высшей математики является математический анализ. Это объемная и интересная наука! И ее изучение всегда начинается с главы «Введение в математический анализ». В этой короткой теме Вы познакомитесь с элементами введения в математический анализ. 

Понятие функции является центральным понятием математики и не только математического анализа. Вспомним школьное определение функции.

Если каждому элементу x множества D ставится в соответствие единственный элемент y множества E,  то говорят, что на множестве D задана функция .

  х – аргумент – независимая переменная; y – зависимая; она находится по закону: f.

Множество Dназывается областью определения функции, множество Eназывается множеством  значений функции.

Множество значений аргумента – Ваши личности, множество значений функции – Ваши фамилии. Вот так мы продемонстрировали понятие функции: каждому значению аргумента соответствует единственное значение функции, человек не может иметь две фамилии.

Но математика рассматривает числовые функции, т.е. множества D и Е – числовые множества, которые Вы изучали в теме 1. При этом можно дать и такое определение числовой функции: числовая функция – это множество пар (х,у), среди которых нет пар с одинаковым первым элементом. Вдумайтесь.

Как определяется, задается функция? Прежде всего формулой, по которой по заданному х находится у. Например: f(x) = x² +x +3. Подставим х = 2 получим у = 9

Функция может задаваться не одним аналитическим выражением, а несколькими, например:

Очень часто зависимость одной переменной величины от другой невозможно выразить аналитически, но такая зависимость существует о определяется она в виде таблицы.

 

x	-3	-1	0	3	5	6	8	11	13
y	45	22	12	2	-4	3	13	25	34

 

          В таком случае говорят о таблично заданной функции, общепринятая аббревиатура: ТЗФ Обратите внимание, что среди заданных пар чисел (х;у) нет пар с одинаковым первым элементом, в таком случае ТЗФ не являлись бы функцией.

       Запишите еще определение числовой функции: числовая функция – множество пар (х;у), среди которых нет пар с одинаковым первым элементом.

И, наконец, когда не удается найти аналитического выражения для , найти множество пар (х;у), то функцию можно задать графически, т.е. ее графиком. Вспомните свою кардиограмму, перо самописцев в самых различных приборах.

 

       Рассмотрим понятия, выражающие т.н. общие свойства функций.

Монотонность. Если для х₁, х₂, принадлежащих интервалу (a;b) и удовлетворяющих условию х₁, < х₂ следует f(х₁) < f(х₂), то, говорят, что на (a;b) эта функция возрастает. Или, как говорили в школе, если большему значению аргумента соответствует большее значение функции, то функция возрастает. Самостоятельно сформулируйте определение убывающей функции. Если функция только возрастает или только убывает в области определения, то о такой функции говорят, что она монотонна. Так линейная функция, степенная с нечетным показателем являются монотонными, а популярная у = х² монотонной не является, т.к. при x < 0 она убывает, а при x > 0 она возрастает.

 

Ограниченность. Пусть на D задана функция . Если существуют такие числа m и M, что для всех х  D, что m ≤  ≤ M, то говорят, что функция ограничена в области определения. Различают и такие понятия, как ограниченность снизу и ограниченность сверху. Так,  у = х³ – неограниченная функция, у = х² – ограничена снизу, т.к. она неотрицательна в области определения. у = Sinx и y = Cosx – ограниченные функции, т.к. они принимают значения только из отрезка [-1; 1] – это их множество значений

Четность и нечётность. Функция называется четной, если ее область определения симметрична относительно х = 0 и ;

Функция называется нечетной, если ее область определения симметрична относительно х = 0 и .

График чётной функции симметричен относительно оси ординат, а нечётной – относительно начала координат.

Яркие «представители» четных функций: у = х², y = Cosx, , нечетных у = х³,

у = Sinx, , . Для многих функций нет смысла говорить об их четности – нечетности. Так функция  не относится ни к четным, ни к нечетным, потому как ее область определения несимметрична относительно нуля. Такие функции называют функциями общего вида.

Какова методика определения четности – нечетности функции? Рассмотрим примеры.

Подставим в функцию вместо х -х, будем иметь:

 Получили определение нечетной функции, вывод: функция нечетная.

 Подставим в функцию вместо х -х, будем иметь:

Получили определение четной функции, вывод: функция четная.

 

Периодичность. Функция  называется периодической, если существует такое число Т, что для всех х из области определения выполняется равенство:

Очевидно, что если существует такое число Т, называемое периодом, то число nT, где n – целое число, также является периодом этой функции. Важнейшие представители периодических функций – тригонометрические функции, которые Вы будете изучать подробно в теме 4. В качестве дополнительного домашнего задания попробуйте построить график функции: дробная часть числа х: это разность между аргументом х и ближайшим к нему целым числом, стоящем на числовой прямой слева от него.

       Рассмотрим практические задачи на отыскание области определения некоторых функций. Заметим, что многочлен определен на всем множестве действительных чисел:       D = R. Так для функции у = х² + 6х – 7 D = R. Дробно – рациональная функция определена для всех х, при которых ее знаменатель отличен от нуля. Например:

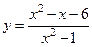 областью определения будет все множество действительных чисел, отличных от -1 и 1. На языке интервалов D = (-∞; -1) (-1; 1) (1; ∞)

Рассмотрим другие примеры. Найти область определения функций.

Очевидно, что функция существует только для тех значений х, которые удовлетворяют неравенству: 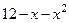 > 0

 

Ответ: D = (-4; 3). Воспользовались методом интервалов, изученным в прошлой теме.

Очевидно, что функция существует только для тех значений х, которые удовлетворяют системе неравенств

                                                                 x + 5 ≥ 0

                                                                 x – 1 ≠ 0 Откуда х ≥ -5 и x ≠ 1 Объединяя эти

 

неравенства, имеем ответ: D = [-5; 1) (1; ∞).

Самостоятельно выполните упражнения из сборника: с.24 № 1.8 – 1.13 

Понятие об обратной функции. Очень важное и глубокое понятие. Будьте внимательны.

Пусть дана функция у = х³Вспомним, что она монотонная: каждому значению аргумента соответствует единственное значение аргумента и наоборот: каждому значению функции соответствует единственное значение аргумента (только для монотонных функций!). Будем далее считать независимой переменной у, а х – его функцией, выразим х через у. 

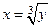 и заменим, как то принято обозначать аргумент и функцию, х на у и у на х, получим

. Вот эти две функции у = х³,  и называются взаимно обратными.

Построим графики этих функций и убедимся, что они симметричны относительно биссектрисы 1-3 координатных углов. Запомните это свойство графиков всех взаимно обратных функций. В дальнейшем Вы будете строить обратные функции по мере их изучения.

 

Но как быть, если функция, для которой надо построить обратную не является монотонной? Например, необходимо построить обратную для у = х², которая немонотонна. Для этого необходимо так задать область определения исходной функции, на которой она стала бы монотонной. Если для функции у = х² положить D = [0; ∞), то на этом луче она монотонно возрастает, а значит имеет обратную. Очевидно, это  Построим их графики и убедимся, что они симметричны относительно биссектрисы 1-3 координатных углов.

Поработайте самостоятельно.

Постройте обратную функцию для монотонной линейной функции у = 3х, постройте их графики.

Определив функцию  на

D = [0; ∞), постройте для нее обратную функцию.

 

 

И заключительный вопрос настоящего урока: приращение аргумента и приращение функции.

Пусть задана функция . При х = х₀ она принимает значение .

х₀  - на оси ОХ в точке А, у₀ – на оси ОУ в точке N. Дадим х приращение Δх = АВ, получим новое приращенное значение аргумента (в точке В) х = х₀ + Δх

Вычислим приращенное значение функции  на оси ОУ – точка М, т.е. длина отрезка ВЕ.

Естественно, что отрезок DE и будет являться приращением функции в точке х₀, если приращение аргумента равно Δх.

Т.е. Δf(x₀) = -

Итак, приращение функции есть разность между приращенным значением функции и первоначальным (отрезок DE).

Обратите внимание, что для возрастающей функции DE > 0, а для убывающей функции АС будет больше DE, поэтому разность DE – АС < 0 и Δf(x₀) < 0.

Сделайте самостоятельно схематический чертеж убывающей функции и укажите Δf(x₀).

Вычислим приращение функции f(x) = х² + 2х +5 при x₀ = 2 и Δx = 0,1 x₀ + Δx = 2,1

По формуле Δf(x₀) = -  = (будем иметь) = -  =

2,1² + 2*2,1 + 5 – (2² + 2*2 +5) = (применяем микрокалькулятор) = 0,61

Поставим задачу отыскать приращение функции не в конкретной точке x₀, а в произвольной х, т.е. выведем формулу приращения в общем виде:

Δf(x) = -  = (х + Δx)² +2(х + Δx) + 5 - х² - 2х -5 = х² + 2х Δx + (Δx)² +2х Δx +5 - х² - 2х -5 =  2х Δx + (Δx)² +2 Δx = 2х Δx + 2 Δx + (Δx)² = 2(х + 1)Δx + (Δx)² – это и есть приращение функции в общем виде: Δf(x) = 2(х + 1)Δx + (Δx)². Подставим х = 2, Δx = 0,1 получим Δf(x) = 0,61 – все верно.

Выполните задание №8 8.4-8.8.8

 

Контрольные вопросы

1) Дать определение функции. 2) Что такое область определения? 3) Что означает понятие «ограниченность функции»? 4) Какие функции называются монотон­ными? 5) Что можно сказать о симметричности гра­фиков чётных и нечётных функций? 6) Какова методика определения четности – нечетности функции? 7) Какие функции периодические и как это записать? 8) Раскрыть понятия приращения аргумента и приращения функции. 9) Для каких функций возможно построить обратную? 10) Сформулировать алгоритм построения обратной функции.

 

Домашнее задание. Сборник: тема 2 №№ 1.8, 8.1-8.3

 

Поделиться:

Воспользуйтесь поиском по сайту: