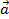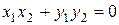|
Тема 2. Проекция вектора на ось. Координаты вектора. Действия над векторами с заданными координатами.
|
|
|
|
Раздел 1_2 - Аналитическая геометрия. Вектор
Тема 1.1 Вектор. Действия над векторами, заданными длиной и направлениями
Определение 1. Величины, которые полностью определяются своими численными значениями, называются скалярными.
Например: площадь, длина, объем, температура, работа, масса.
Определение 2. Некоторые величины определяются не только своими числовыми значениями, но и направлением. Такие величины называют векторными.
Например сила, скорость, ускорение. Векторная величина геометрически изображается с помощью вектора.
Определение 3. Вектор – это направленный отрезок. Вектор обозначается двумя способами.
|
|

 1) 2)
1) 2)
 | |||||||
| |||||||
| |||||||
| |||||||
Определение 4. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 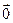 . Нулевой вектор направления не имеет.
. Нулевой вектор направления не имеет.
Действия над векторами

I. Сложение векторов
1. Правило треугольника
Возьмем произвольную точку О и построим вектор  . От точки А отложим вектор
. От точки А отложим вектор  . Вектор
. Вектор  , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов  и
и  :
: 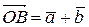



2
| |
|
 и
и  . Возьмем произвольную точку О и построим вектора
. Возьмем произвольную точку О и построим вектора  и
и  . Достроим до параллелограмма. Диагональ выходящая из точки О называется суммой векторов.
. Достроим до параллелограмма. Диагональ выходящая из точки О называется суммой векторов.
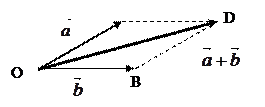 |
3. Правило многоугольника
Это правило используется для построения суммы более чем двух векторов. Все вектора откладываются друг за другом.
|
|
|
Построим сумму векторов  .
.
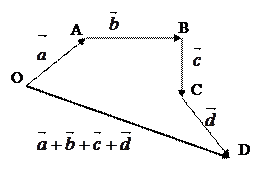 Возьмем произвольную точку О и построим вектор
Возьмем произвольную точку О и построим вектор  . От точки А отложим вектор
. От точки А отложим вектор 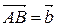 , далее
, далее  ,
, 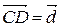 . Вектор
. Вектор  , соединяющий начало первого с концом последнего, называется суммой векторов, т.е.
, соединяющий начало первого с концом последнего, называется суммой векторов, т.е.  .
.
II. Разность векторов
Построим разность векторов  и
и  . Возьмем произвольную точку О и построим вектора
. Возьмем произвольную точку О и построим вектора  и
и  . Вектор
. Вектор  , соединяющий конец второго с концом первого вектора
, соединяющий конец второго с концом первого вектора  .
.
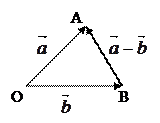

III. Умножение вектора на число
Умножение вектора 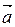 на число
на число  , есть вектор, длина которого равна
, есть вектор, длина которого равна  , а направление совпадает с направлением
, а направление совпадает с направлением  , если
, если  , и противоположно направлен, если
, и противоположно направлен, если  .
.
Построить  ,
,  ,
,  .
.
 |
Определение 5. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых и их направление либо совпадает, либо они противоположно направлены.
IV. Скалярное произведение векторов
Скалярное произведение двух ненулевых векторов  и
и 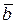 - это число, равное произведению длин этих векторов на косинус угла между ними.
- это число, равное произведению длин этих векторов на косинус угла между ними.
 |
 .
.
 .
.
 .
.
Задача №1
Дано:
 | |||||
 | |||||
 | |||||


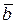
 ..
..
Построить
 .
.
 1.
1. 
|
 2.
2. 
Для проверки: 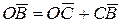
Задача №2
Дано:
 |

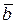
 .
.
Построить 
 |

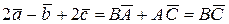
Упражнения
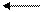

 №1. Дано:
№1. Дано: 
|
|
|
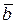
 .
.
построить 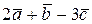
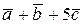
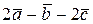


 №2. Дано:
№2. Дано: 
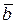
 .
.
построить 
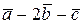



 №3. Дано:
№3. Дано: 
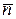
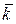
.
построить 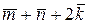


 №4. Дано:
№4. Дано:
 |  | ||||
 | |||||

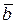


построить 

№5. Дано:




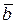



построить 


№6. Дано:






построить 

№7. Дано:




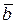

построить 


№8. Дано:





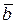


|
|
|
построить 

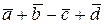

№9. Дано:  .
.
Найти  , если угол между векторами
, если угол между векторами  и
и 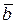 равен:
равен:
а) 450; б) 600; в) 1200; г) 1800.
№10. Дано: 
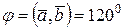 .
.
Найти:
а)  ; б)
; б)  ; в)
; в)  .
.
№11. Возьмите два произвольных вектора  и
и 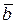 , построить
, построить
1)  ; б)
; б) 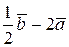 ; 3)
; 3)  ; 4)
; 4)  .
.
№12. В параллелограмме ABCD:
 ;
; 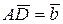 . О – точка пересечения диагоналей.
. О – точка пересечения диагоналей.
Выразите вектора 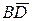 ,
,  ,
,  ,
, 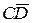 через
через  и
и 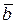 .
.
№13. Даны векторы  ,
, 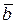 и
и  , причем
, причем  ,
,  ,
,  ,
,
 .
.
Найти:
1)  ;
;
2)  .
.
№14. Вычислите:
1)  ;
;
2)  .
.
Тема 2. Проекция вектора на ось. Координаты вектора. Действия над векторами с заданными координатами.
 Определение 1. Проекцией вектора
Определение 1. Проекцией вектора  на ось
на ось  называется число, равное величине отрезка
называется число, равное величине отрезка  , где точки
, где точки  .и
.и  являются проекциями точек
являются проекциями точек  и
и 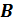 на ось
на ось  .
.
 В D
В D
А 
C 
А1 В1 D1 C1
Длина этого направленного отрезка берется со знаком «+», если направление отрезка и оси совпадают, и со знаком «–», если их направления противоположны


Определение 2. Проекция вектора  на ось
на ось  равна длине этого вектора, умноженной на косинус угла
равна длине этого вектора, умноженной на косинус угла  между осью и вектором,
между осью и вектором,  .
.
|
|






 Рассмотрим вектор
Рассмотрим вектор  , где
, где  . Спроецируем вектор
. Спроецируем вектор 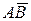 на ось координат.
на ось координат.
 У
У
у2 В
у1
А


 |
 х1 х2 Х
х1 х2 Х 
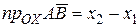

 .
.
Определение 3. Координаты вектора это проекции вектора на соответствующие оси координат. Если начало вектора совпадает с началом координат, то вектор называется радиус-вектором.
|
|
|
Определение 4. Базис плоскости – это два неколлинеарных вектора этой плоскости, взятые в определенном порядке. O, 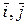 ;
;  ;
;  . Аналогично, базис пространства: O,
. Аналогично, базис пространства: O,  ;
;  ;
;  .
.

 – разложение вектора по базису
– разложение вектора по базису
| на плоскости | в пространстве |
 
|
 
|
|
1) Длина вектора | |

|

|
|
2) Скалярное произведение векторов | |

|

|
|
3) Угол между векторами | |

|

|
|
4 ) Сумма / разность векторов | |

| 
|
|
5 ) Умножение вектора на число | |
 , , 

|

|
|
6) Условие параллельности векторов | |
|
| |
| 7) Условие перпендикулярности векторов | |
|
| |
Проекция вектора  на вектор
на вектор 
 .
.
Для двух векторов с известными координатами:
 и
и  имеет место следующее равенство:
имеет место следующее равенство:

 .
.
Принимаем во внимание, что:  , поскольку это есть скалярные квадраты, например
, поскольку это есть скалярные квадраты, например  ,
,
 , т.к. это есть скалярные произведения перпендикулярных векторов.
, т.к. это есть скалярные произведения перпендикулярных векторов.
Замечание: скалярное произведение двух векторов равно сумме парных произведений одноименных координат векторов.
Условие перпендикулярности векторов: для того, чтобы два вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю, т.е. сумма парных произведений их одноименных проекций равнялась нулю.
Задача
Дано:  ;
;
 ;
; 
 .
.
Найти: 1) координаты вектора  ;
;
2) длину вектора 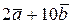 ;
;
3) скалярное произведение векторов 
 .
.
Решение
1) 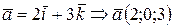



+

+

_______________________________________________________

 .
.
2) Чтобы найти длину вектора 
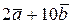 , нужно сначала найти координаты этого вектора:
, нужно сначала найти координаты этого вектора:



+

___________________

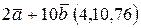
 .
.
3) Чтобы вычислить скалярное произведение векторов, нужно найти их координаты:
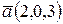
–


__________________

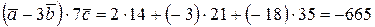 .
.
Задача №2
Дано:  ;
;
 ;
;
 ;
;
 .
.
Найти:
1) длину вектора  ;
;
2) угол между векторами  и
и  .
.
Решение
1)  ;
;
 .
.
2)  $
$
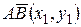
 $
$
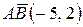 ;
;  4
4
 ;
;
 ;
;
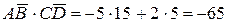 ;
;
 .
.
Задача № 3:
Дано: вектора  и
и 
Найти: проекцию вектора  на вектор
на вектор  .
.
Решение:
Найдем скалярное произведение этих векторов
|
|
|

Найдем модуль вектора 

Найдем проекцию вектора  на вектор
на вектор 

Ответ: 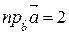 .
.
Упражнения
№1. Найти угол между векторами  и
и  .
.
№2. Доказать, что  с вершинами
с вершинами  ,
,  и
и  равнобедренный и прямоугольный.
равнобедренный и прямоугольный.
№3. Найти длину вектора  , если
, если  и
и  .
.
№4. При каких значениях 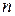 векторы
векторы  и
и  коллинеарны?
коллинеарны?
№5. Определить при каких значениях  вектора
вектора  и
и  взаимно перпендикулярны?
взаимно перпендикулярны?
№6. Даны вершины 
 ,
,  и
и  . Определить его внутренние углы.
. Определить его внутренние углы.
№7. Дано:  ;
;
 ;
;
 .
.
Найти:
1. координаты вектора  ;
; 
2. длину вектора 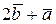 ;
;
3. скалярное произведение векторов  4
4
4. угол между векторами  и
и  .
.
№8. Дано:  ;
;
 ;
;
 .
.
Найти: 1. координаты вектора  ;
; 
2. длину вектора  ;
;
3. скалярное произведение векторов  и
и 
4. угол между векторами  и
и  .
.
№9. Дано:  ;
;
 .
.
Найти:
1. 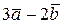 ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  .
.
№10. Найти скалярное произведение векторов  и
и  , и угол между ними:
, и угол между ними:
1)  ; 2)
; 2)  ;
;
2)  ; 2)
; 2)  .
.
№11. При каких значениях  вектора
вектора  и
и  взаимоперпендикулярны?
взаимоперпендикулярны?
№12. Найти координаты вектора  Б коллинеарного вектора
Б коллинеарного вектора  , если:
, если:
1)  ;
;  ;
;
2)  ;
;  .
.
№13. Дан треугольник с вершинами 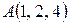 ,
,  и
и  .
.
Доказать, что угол  тупой.
тупой.
Зачетная работа
|
|
|