 |
Правило треугольника (правило Сарруса )
|
|
|
|
Лекция определители
Определители второго порядка
Выражение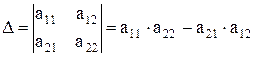 
(1) называется определителем 2-го порядка.
Числа 
– это элементы определителя. Определитель 2-го порядка имеет две строки и два столбца.
Индексы, стоящие внизу соответствующего элемента, означают номер строки и номер столбца определителя, на пересечении которых стоит указанный элемент. Таким образом, 
- элемент, стоящий на пересечении i – й строки и j – го столбца.
Например, элемент 
стоит в первой строке и втором столбце определителя.
В определителе рассматриваются две диагонали: главная, которая состоит из элементов 
и 
, и побочная, которая состоит из элементов 
и .
Пример 1: Вычислим определитель второго порядка
Свойства определителей
Формулируя свойства, мы не будем указывать порядок определителя, так как эти свойства справедливы для определителей любого порядка, но доказательства свойств проведём для определителей 2-го порядка.
1. Определитель не меняет своего значения при замене всех его строк соответствующими столбцами, то есть 
.
Действительно, разложим определитель, стоящий справа, по элементам первой строки: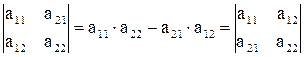 
.
Таким образом, получаем выражение, соответствующее исходному определителю, что и требовалось доказать.
Замечание: Определитель в правой части формулы называют транспонированным по отношению к определителю в левой части этой формулы.
2. Если переставить две строки (или столбца) определителя, то абсолютная его величина не изменится, а знак изменится на противоположный 
.
Действительно, разложим определитель, стоящий справа, по элементам первой строки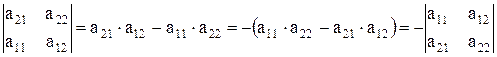 
, после вынесения общего множителя 
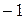в скобках получаем выражение, соответствующее исходному определителю, что и требовалось доказать.
|
|
|
Из свойства 2 вытекает следующее свойство.
3. Если две строки (столбца) определителя равны, то определитель равен нулю.
Действительно, рассмотрим определитель с равными строками 
, разложим его по элементам первой строки 
, что и требовалось доказать.
4. Общий множитель элементов какого-либо ряда (строки или столбца) определителя можно выносить за знак определителя.
Действительно, рассмотрим определитель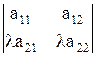 
. Разложим его по элементам первой строки 
. Что и требовалось доказать.
5. Если в какой-либо строке (или столбце) определителя все элементы равны нулю, то определитель равен нулю.
Действительно, рассмотрим определитель 
, что и требовалось доказать.
6. Если элементы какого-либо ряда определителя пропорциональны элементам параллельного ряда, то определитель равен нулю.
Пусть, например, элементы первой и второй строк определителя пропорциональны. Тогда имеем 
. Что и требовалось доказать.
7. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель можно представить в виде суммы двух определителей, у которых все ряды, кроме данного, совпадают, а в данном ряду в первом определителе стоят первые, а во втором – вторые слагаемые.
Допустим, что элементы первой строки определителя являются суммами двух слагаемых. Тогда имеем: 
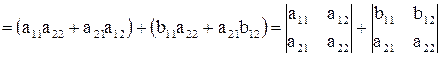. Что и требовалось доказать.
8. Величина определителя не изменится, если к элементам какого-либо ряда (строки или столбца) определителя прибавить или отнять элементы параллельного ряда, умноженные на одно и то же число (то есть составить линейную комбинацию строк или столбцов).
Для доказательства этого рассмотрим определитель 
, к элементам второй строки прибавим соответствующие элементы первой строки, умноженные на одно и тоже число.
|
|
|
. Что и требовалось доказать.
Определители 3-го порядка
Выражение 
(2) называется определителем 3-го порядка.
В таком определителе элементы 
составляют главную диагональ, а элементы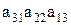 
- побочную диагональ.
Кроме вычисления определителя по приведенной формуле (2) возможно его вычисление согласно выражению:
Правило треугольника (правило Сарруса)
(3)
Пример 2. Вычислить определитель третьего порядка двумя способами
Способ 1:
Способ 2:
.
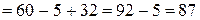Замечание: Если правило треугольника применить к определителю треугольного вида 
, то этот определитель будет равен произведению элементов главной диагонали 
.
С целью введения более эффективных способов представления определителей третьего и более высоких порядков, рассмотрим некоторые дополнительные определения.
Минором 
элемента определителя n-го порядка называется определитель n-1-го порядка, получающийся из данного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Например, минором элемента определителя третьего порядка будет являться выражение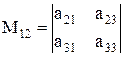 
.
Таким образом, разложение определителя третьего порядка по элементам первой строки можно представить как
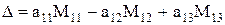
Алгебраическим дополнением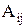 
элемента определителя n-го порядка называется минор этого элемента, взятый со знаком плюс, если элемент стоит на пересечении строки и столбца с четной суммой номеров, и со знаком минус, если элемент стоит на пересечении строки и столбца с нечетной суммой номеров.
Часто для определения знака алгебраического дополнения используется формула:
. (4)
Для определителя 3-го порядка знаки алгебраических дополнений можно определить по таблице:
Например, алгебраическим дополнением элемента 
определителя третьего порядка будет являться его минор, взятый со знаком минус 
.
Таким образом, разложение определителя третьего порядка по элементам первой строки можно представить как
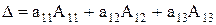
Теорема: (Теорема разложения) Определитель 3-го порядка равен сумме парных произведений элементов какого-либо ряда (строки или столбца) определителя на их алгебраические дополнения.
|
|
|
Таким образом, имеет место шесть разложений:
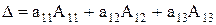
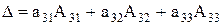(5)
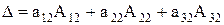
Теорема: (Теорема Лапласа) Определитель квадратной матрицы равен сумме произведений элементов любого ряда определителя на их алгебраические дополнения.
Замечание. сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения элементов параллельного ряда равна нулю.
Пример 3. Вычислить определитель третьего порядка путем разложения по элементам третьей строки
|
|
|
