 |
Физическая модель вязко – пластичноготела с последовательным соединением.
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФГБОУ ВО МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ
Имени К.Г.Разумовского (ПКУ)
Кафедра «Машины, аппараты и процессы пищевых производств»
Реферат по дисциплине
Физико – механические свойства пищевых продуктов
Тема: «Реология»
Выполнил студент: Медведев А.М.
Институт «Технологический менеджмент»
Направление подготовки: 15.03.02
Курс 3
Проверил: Калошин Ю. А.
Оценка ________________
Москва – 2017
Задание.
1. Дать описание идеальных реологических моделей. Указать их физические свойства, математические модели и «кривые» течения.
2. Определить объёмный расход Q при продавливании под давлением Р исследуемой жидкости через канал круглого сечения, длиной L и радиусом R.
L = 0.16м
R = 0,016
Р = 2,5*105
3. Привести схемы приборов для определения реологических характеристик. Дать краткое описание их работы, построение по кривым течения на основании исследований.
4. Выполнить задание: Определить объёмный расход Q под давление P – исследуемой не ньютоновской жидкости через канал круглого сечения. Канал имеет следующие характеристики L=0.16; R=0.016; Р=2.5*105;
Реология – занимается изучением деформации различных тел при течении по каналам различной формы.
Реология изучает основные свойства текучих тел, такие как: упругость, пластичность, вязкость.
Реологические модели.
1. Идеально упругое тело. Тело Гука.
Физическая модель идеально упругого тела.
Физической моделью идеально упругого тела может быть спиральная пружина имеющая следующие свойства: при придании нагрузки растягивается, а при снятии возврвщается в исходное положение.
|
|
|
Математическая модел.
Математическая модель, описывает поведение идеально упругого тела и записывается следующим образом

где 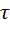 - Касательное напряжение
- Касательное напряжение
G – модуль сдвига
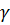 - угол сдвига (градиент смещения)
- угол сдвига (градиент смещения)
«Кривая» течения.
«Кривая» течения описывает деформацию идеально упругих тели имеет вид
 Y
Y 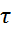
 |
 X
X 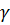
2. Идеальное пластическое тело. Тело Сен-Венана-Кулона.
Идеальной физической моделью пластического тела может служить тело движущиеся по плоскости, преодолевая силу трения, независимо от силы нормального давления действующего на него.





 N
N








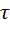
T=f * N, Н
где:
f - коэффициент трения
N – сила давления
 T
T


Математическая модель идеально пластического тела.
 =
=  т, Па где:
т, Па где:
 - напряжение сдвига приложенное к нему (телу)
- напряжение сдвига приложенное к нему (телу)
 т – Напряжение при котором тело начинает течь
т – Напряжение при котором тело начинает течь
Реологическая «кривая» идеально пластического тела.
Реологическая «кривая» идеально пластического тела описывает его диформацию и выглядит так:
 Y
Y 


X 
Идеально вязкая жидкость. Ньютоновская жидкость.

















 изической моделью идеально вязкой жидкости является перфорированный поршень, перемещающийся с цилиндре с жидкостью. Ньютоновская жидкость обладает постоянной вязкостью.
изической моделью идеально вязкой жидкости является перфорированный поршень, перемещающийся с цилиндре с жидкостью. Ньютоновская жидкость обладает постоянной вязкостью.


 | |
 |
Математическая модель.
Математическая модель для идеально вязкой жидкости записывается следующим образом
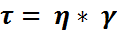 ; Па где:
; Па где:
 – напряжение сдвига
– напряжение сдвига
 – Коэффициент вязкости тела
– Коэффициент вязкости тела
 - ?
- ?
Реологическая кривая.


X 
 |



X 
Коэффициент вязкости в данном случае вычисляется по формуле:
tg  =
= 
Упруго - в
Вязкое тело. Тело Кельвина.
Физическая модель.
В моделе, упругое и вязкое тело соединяются параллельно.
Выглядит данная модель следующим образом.



























|
|
|
 |

Математическая модель тела Кельвина.

Где
G – напряжение сдвига упругого тела.
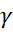 – скорость сдвига
– скорость сдвига
 - пластическая вязкость
- пластическая вязкость
Вязко – пластичное тело.
Вязко – пластичные тела (конфеты «Промене») бывают двух видов: с параллельным и последовательным соединением. Данные соединения проявляют различные свойства.
Физическая модель вязко – пластичного тела с параллельным соединением.

































 |

 «Кривая» течения.
«Кривая» течения.
y 
 |



 0
0
 x
x 
Математическая модель.
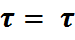 0 +
0 +  *
* 
Физическая модель вязко – пластичноготела с последовательным соединением.
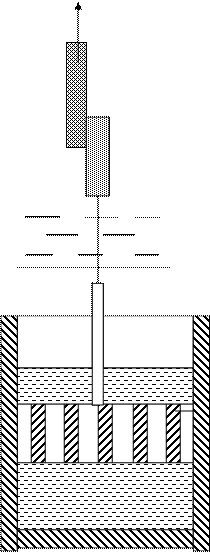 |

 Кривая течения.
Кривая течения.
y 





 0
0


x 
Математическая модель.

 *
*  при
при  <
<  0
0
 =
=  0 при
0 при  =
=  0
0
«Кривая» течения.


 y
y 
 |  |
 Q
Q
 1
1  2 x
2 x 
 1
1  2
2
Задача: Определить объёмный расход Q под давление P – исследуемой не ньютоновской жидкости через канал круглого сечения.
Канал имеет следующие габариты: длина L = 0,16м и радиус R = 0,016м

160мм
 | |||||
 | |||||
 |

Приборы для определения реологических характеристик пищевых масс.
Ротационный вискозиметр.
 | |||
 | |||






 исследуемая жидкость
исследуемая жидкость
 |
Работа вискозиметра.
Исследуемая жидкость помещается в зазоре между подвижным и не подвижным цилиндрами, за счёт тепловой рубашки она темперируется до заданной температуры, начинается вращение цилиндра с заданной угловой скоростью. При работе аппарата измеряется крутящий момент на вращающемся цилиндре и его угловая скорость. По заданным параметрам рассчитывается напряжение и скорость сдвига, при заданной температуре. Получаем точку на кривой течения.
Напряжение сдвига рассчитывается по следующей формуле.
 M/2
M/2  R3 где
R3 где
М – крутящий момент; Н*м
R – радиус в метрах
Скорость сдвига определяется формулой
 R/a где
R/a где
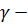 скорость сдвига
скорость сдвига
 – угловая скорость
– угловая скорость
а –расст. Между подвижным и неподвижным цилиндром
Реологическая кривая.
 |




 3
3




 2
2
 1
1

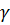
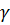 1
1 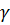 2
2 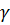 3
3
Капилярный вискозиметр.
 В таких вискозиметрах исследуемая жидкость продавливается через капилляр, соотношение между длиной и диаметром должно быть больше или равно 10.
В таких вискозиметрах исследуемая жидкость продавливается через капилляр, соотношение между длиной и диаметром должно быть больше или равно 10.
|
|
|
 е/d
е/d  P
P
 |

 исследуемый материал
исследуемый материал
 |  | ||||
 | |||||


 L d
L d
При исследование на капиллярном вискозиметре необходимо знать длину капилляра и его диаметр, расход исследуемой жидкости Q м3/сек
Напряжение рассчитывается по формуле
 P*R/2l
P*R/2l
Скорость определяют формулой
 4Q/
4Q/  R2
R2
Конический пластометр.
Данный прибор предназначен для определения напряжения сдвига у материалов имеющих высокую вязкость.
 Р,Н
Р,Н






 3
3


 4
4 
 |  | ||||
 | |||||





 h
h




 Исследуемый материал
Исследуемый материал



 2 1
2 1

1. Тепловая рубашка; 2. Ёмкость для исследуемого материала; 3. Шток; 4. Сменный конус;  - угол конуса
- угол конуса
Работа прибора.
Исследуемый материал загружается в ёмкость 2, темперируется при помощи тепло рубашки, после чего к штоку 3 прикладывают заданное усилие Р, которое позволяет штоку с конусом внедриться в исследуемый материал. После шток поднмается вверх и измеряется глубина внедрения конуса. Углы конуса  могут иметь значение: 30, 35, 45, 50, 60, 70, 90.
могут иметь значение: 30, 35, 45, 50, 60, 70, 90.
Предельное напряжение сдвига находят по формуле
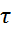 n=K*p/h2 где
n=K*p/h2 где
К – коэффициент учитывающий угол при внедрение конуса
Р – усилие внедрения штока в материал; h – высота внедрения штока в исследуемый материал в метрах
Индвидуальное задание.
Задача: Определить объёмный расход Q под давление P – исследуемой не ньютоновской жидкости через канал круглого сечения. Канал имеет следующие характеристики L=0.16; R=0.016; Р=2.5*105
Расчет производится по следующей формуле.
Q =  R3*n/3n+1*(R*P/2*K*L)
R3*n/3n+1*(R*P/2*K*L)
3,14*0.0163*0.5/3*0.5+1*(0.016*2.5*105/2*700*0.16) = 0.000046 м3/с
Переводим метры кубические в кубические милиметры, таким образом расход при заданных условиях будет равен 46000мм3/сек  460гр/с
460гр/с
Вывод: Пользуясь выше перечисленными моделями реальных тел, становится возможным рассчитывать мощностные характеристики различного оборудования применяемого как на пищевом производстве так и на различном другом производстве
|
|
|
|
|
|


