 |
Расчеты числовых характеристик времени безотказной работы элементов при экспоненциальном и нормальном законах распределения
|
|
|
|
Рассчитать и построить функции P(t), Q(t), λ(t), f(t) для нормального и экспоненциального законов распределения.
Нормальный закон распределения является предельным законом для случайных величин, которые имеют другие законы распределения и случайным образом воздействуют на объект. Нормальный закон в теории надежности используется для определения погрешностей. Для нормального закона задается функция плотности времени распределения безотказной работы равна
,
где s – среднеквадратичное отклонение;
Т ср – среднее время безотказной работы элемента
Вероятность отказа 
определяется с помощью таблиц Лапласа, показанной в таблице 2.
Таблица 2.
Значения приведенной функции Лапласа
| x | Ф *(х) |
| –3 | |
| –2 | 0,0228 |
| –1 | 0,1587 |
| 0,5 | |
| 0,8413 | |
| 0,9772 | |
Вероятность надежной работы P(t)=1-Q(t).
Интенсивность отказов
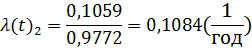
Результаты вычислений сводятся в таблицу 3.
Таблица 3.
| t | f (t),1/год | P (t) | Q (t) | λ (t),1/год | |
| Т –3 σ | 0,0003 | 0,0003 | |||
| Т –2 σ | 0,1059 | 0,9772 | 0,0228 | 0,1084 | |
| Т – σ | 0,4746 | 0,8413 | 0,1587 | 0,5641 | |
| Т | 0,7824 | 0,5 | 0,5 | 1,5649 | |
| Т +1 σ | 0,4746 | 0,1587 | 0,8413 | 2,9904 | |
| Т +2 σ | 0,1059 | 0,0228 | 0,9772 | 4,6444 | |
| Т +3 σ | 0,0087 | 
|
Зависимость числовых характеристик от времени при нормальном законе распределения представлена на рисунке 3.
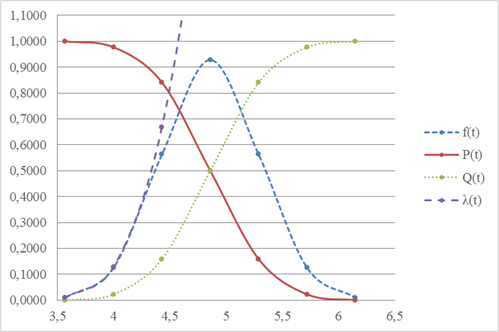
Рис.3
Для экспоненциального закона распределения принимается интенсивность отказов l(t) = l = const, тогда вероятность безотказной работы равна
P (t) =e-lt
Q (t) = 1 –P (t),
При расчетах интенсивность отказов λ берется как среднее значение, рассчитанное в задаче № 1, т.е.
, где k =10;
; 
; 
; 
; 
.
Зависимость числовых характеристик от времени при экспоненциальном законе распределения представлена на рис. 4.
|
|
|
Рис.4
Результаты расчетов параметров надежности при экспоненциальном законе распределения сводятся в таблицу 4.
Таблица 4.
| t | f (t),1/год | P (t) | Q (t) | |
| 0,3889 | ||||
| 0,5 Т | 0,1279 | 0,3288 | 0,6712 | |
| Т | 0,0421 | 0,1081 | 0,8919 | |
| 2 Т | 0,0045 | 0,0117 | 0,9883 | |
| 3 Т | 0,0005 | 0,0013 | 0,9987 |
5. Определение доверительных интервалов для числовых оценок параметров надежности P(t), Q(t), f(t), λ(t)
Для оценок параметров надежности P (t), Q (t), f (t), λ (t), рассчитанных в задании № 1 вычислить и построить доверительные интервалы для заданной доверительной вероятности.
Любое значение искомого параметра, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайности. Такое приближенное значение называется оценкой параметра.
– оценка (среднее значение) для параметра а; 
.
Чтобы дать представление о точности и надежности оценки пользуются доверительным интервалами и доверительными вероятностями.
Доверительная вероятность b – это вероятность того, что случайный интервал Iβ накроет параметр а.
1. Вычисляется оценка 
(среднее значение):
,
где k – число значений случайной величины λ, k =10.
2. Определяется несмещенная оценка 
(дисперсия, вычисленная по опытным данным):
.
3. Дисперсия выборочной средней величины
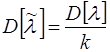
4. Определяется оценка σ (среднеквадратичное отклонение):
.
5. Значения доверительной вероятности 
=0,93
6. Определяется отклонение ε:
,
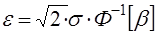где b – доверительная вероятность.
7. Определяются нижняя и верхняя доверительные границы доверительного интервала
.
Доверительный интервал:
Аналогично определяются доверительные интервалы для числовых оценок параметра P (t), Q (t), f (t).
Все данные сводятся в таблицу 5.
Таблица 5.
| λ (t) | Q (t) | P (t) | f (t) | |
| 0,3889 | 0,49278 | 0,50722 | 0,0933 |
| D[a] | 0,3404 | 0,06732 | 0,06732 | 0,00604 |
| 0,0378 | 0,06732 | 0,06732 | 0,0007 |
| 0,0615 | 0,08205 | 0,08205 | 0,00819 |
| 0,1131 | 0,15084 | 0,15084 | 0,01506 |
| 0,5019 | 0,6436 | 0,6581 | 0,1084 |
| 0,2758 | 0,3419 | 0,3564 | 0,0783 |
|
|
|
Данные интервалы наносятся на графики и показаны на рисунках 5 (а,б),6(а,б).
а)
б)
Рис 5 (а,б)
а)
б)
Рис.6 (а,б)
|
|
|
