 |
Измененный порядок уравнений.
|
|
|
|
Решение
Метод Зейделя - итерационный метод решения системы линейных алгебраических уравнений Ах=b.
Исходный порядок уравнений.
А:=  b:=
b:= 
Сначала проводится преобразование системы Ax=b к виду x=Bx+c, удобному для итераций. Это осуществляется с помощью функций:
x:=lsolve(A,b)
x= 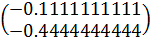
Сначала проводится преобразование системы Ax=b к виду x=Bx+c, удобному для итераций. Это осуществляется с помощью функций

| 
|
B:=PB(A,2) B= 
c:=Pc(A,b,2) c= 
Далее проводится проверка достаточного условия сходимости метода Зейделя. Для сходимости метода Зейделя достаточно, чтобы в каждой строке матрицы B сумма модулей всех элементов была меньше 1

| normB(B,2)=0.25 –условие сходимости выполнено |
Функция, осуществляющая решение системы методом Зейделя:
входные параметры:
B и c - матрица B и вектор правой части c
системы x=Bx+c;
n - порядок матрицы B;
e - точность;
x0 - вектор начального приближения
Решение системы по методу Зейделя находится как предел последовательности  вычисляемой по правилу
вычисляемой по правилу


Результат работы функции решение системы с точностью 0.001:
y:=zeid(B,c,2,0.001,x0)

Проведено 4 итераций для достижения заданной точности.
Графики уравнений СЛАУ с первыми четырьмя итерациями
x:=-0.37,-0.36..0.21

| 
|

Измененный порядок уравнений.
А:=  b:=
b:= 
x= 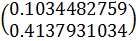
Проведем преобразование системы Ax=b к виду x=Bx+c, удобному для итераций.




normB(B,2)=7 –условие сходимости не выполнено
К такой системе метод Зейделя не применим. Тем не менее проведем несколько итераций, поставив ограничение – не больше 10 итераций.



Процесс расходится.
Графики уравнений СЛАУ с первыми тремя итерациями




1.2 Система четырех Линейных Алгебраических Уравнений (СЛАУ) с четырьмя неизвестными задана своей расширенной матрицей. Решите СЛАУ методом Зейделя с точностью до 0.001.
|
|
|

Решение:


Преобразование системы Ax=b к виду x=Bx+c, удобному для итераций



| 
|

| 
|

| 
|
Проверка достаточного условия сходимости метода Зейделя

 -условие сходимости выполнено
-условие сходимости выполнено
| Начальное приближение | 
|

Результат работы функции решение системы с точностью до 0.001


| Решение: | 
|
Погрешность:



ЗАДАНИЕ 2
Отделить корни уравнения f(x) = 0, используя графико-аналитический метод. Найти корни уравнения с заданной точностью методами бисекций, Ньютона или простых итераций. Выполнить проверку правильности найденных решений, вычислив невязки.
Решение:
1) x3+8x-6=0


Уравнение имеет один корень, заключенный на [0,1].
Корень один так как  при всех x, поэтому f(x) возрастает на R.
при всех x, поэтому f(x) возрастает на R.
Найдем корень уравнения методом бисекций (половинного деления).
Метод бисекции.




Корень уравнения 0.706
2) 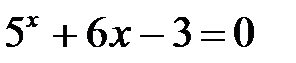
Построим график функции 

|

|

|
Уравнение имеет один корень, заключенный на [0,0.4].
Корень один так как  при всех x, поэтому f(x) возрастает на R.
при всех x, поэтому f(x) возрастает на R.
Найдем корень уравнения методом простых итераций. Уравнение надо привести к виду  :
:


Функция, возвращающая значение корня методом простых итераций:

|

|

|
Результаты работы функции:

|

|
| Корень уравнения |

|

|

|
Корень уравнения, найденный с точностью 0,001 составил 0,251. Для вычисления понадобилось 5 итераций.
Решение найдено правильно, невязка близка к 0.
ЗАДАНИЕ 3
3.1. Используя обобщённые формулы трапеций и Симпсона вычислить определённые интегралы с заданной точностью. Проверку достижения требуемой точности проводить по правилу Рунге.
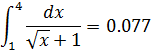
a:=1 b:=4
Формула трапеций для приближённого вычисления определённого интеграла имеет вид
 ,
,
где  ,
,  ,
,  .
.
Функция для вычисления интеграла по формуле трапеций:

Для достижения заданной точности по правилу Рунге будем удваивать n до тех пор, пока  , где
, где  - приближенное значение интеграла, вычисленное при заданном числе отрезков n. Функция, выполняющая эти действия:
- приближенное значение интеграла, вычисленное при заданном числе отрезков n. Функция, выполняющая эти действия:
|
|
|

Результат расчетов:
I:=Int(a,b,0.001)
I=1.5917
Погрешность по сравнению с точным решением составила 0,0001.
Формула Симпсона для приближённого вычисления определённого интеграла имеет вид
 ,
,
где n=2k, первая сумма по нечетным индексам, вторая - по четным.
Функция для расчета интеграла по формуле Симпсона:


Результат расчетов:
I:=Int(a,b,0.001)
I=1.5918
3.2. Используя обобщённую формулу Симпсона, составить таблицу значений функции, заданной в виде интеграла с переменным верхним пределом.
3.2. Используя обобщённую формулу Симпсона, составить таблицу значений функции, заданной в виде интеграла с переменным верхним пределом.

|

|
Решение
Функция для вычисления таблицы значений функции оформим как процедуру
| Вычисление таблицы значений функции |

|
[a,b] – отрезок на котором строится таблица, h – шаг, с которым надо вычислять значение функции,  - точность вычисления.
- точность вычисления.
Выполним вычисления

|

|

|

|
ЗАДАНИЕ 4
4.1. Найти приближённое решение задачи Коши  ,
,  методом Эйлера и методом Рунге-Кутта 4 порядка на заданном отрезке с шагом h = 0.1 (или h = 0,01).
методом Эйлера и методом Рунге-Кутта 4 порядка на заданном отрезке с шагом h = 0.1 (или h = 0,01).
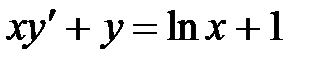 ,
,  ,
, 
Решение
Приведем уравнение к виду 

Для решения дифференциального уравнения методом Эйлера на [a,b] используются формулы:
 ,
,  ,
,  ,
, 
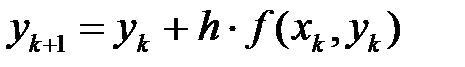 .
.
Функция, рассчитывающая решение дифференциального уравнения методом Эйлера.

Зададим начальные данные:

|

|

|

|

| Приближенное решение |

|

|

|

|

|
Для решения дифференциального уравнения методом Рунге-Кутта используются формулы:

Функция, рассчитывающая решение дифференциального уравнения методом Рунге-Кутта.

| Приближенное решение |

|

|

|

|

|
Получить решение методом Рунге-Кута можно также с помощью встроенной функции

|

|
4.2. Найти приближённое решение задачи Коши  ,
,  ,
,  методами Эйлера и Рунге- Кутта 4 порядка на отрезке [0;1] с шагом h = 0,1 (или h = 0,01).
методами Эйлера и Рунге- Кутта 4 порядка на отрезке [0;1] с шагом h = 0,1 (или h = 0,01).
 ,
,  ,
, 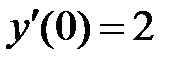
Решение
Для того, чтобы применить к уравнению численные методы Эйлера и Рунге-Кутта, следует свести это уравнение к системе 2-х дифференциальных уравнений 1-го порядка.
|
|
|


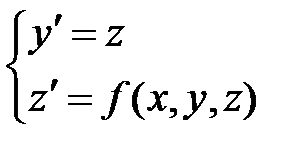 , где
, где 
К полученной системе применяем формулы Эйлера:
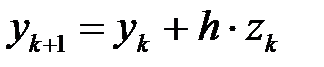 ,
,
 ,
, 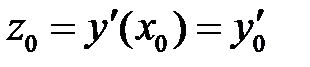
Функция, рассчитывающая решение системы дифференциальных уравнения методом Эйлера.

| Приближенное решение |

|

|

|

|

|

|
Формулы Рунге-Кута для системы уравнений

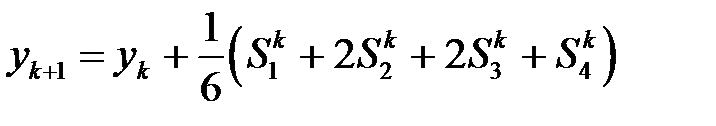

 ,
, 





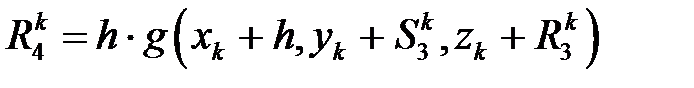
В нашем случае



|

|

|

| Приближенное решение |

|

|

|

|

|

|
Получить решение методом Рунге-Кута можно также с помощью встроенной функции

|

|

|

|

|
|
|
|


