 |
Равномерное движение по окружности.
|
|
|
|
Методическое пособие для подготовки к ЕГЭ по ФИЗИКЕ
Механика
Санкт Петербург, 2014
ПЕРЕЧЕНЬ НЕОБХОДИМЫХ ОПРЕДЕЛЕНИЙ, ФОРМУЛ И УМЕНИЙ ДЛЯ СДАЧИ ЕГЭ ПО ФИЗИКЕ
Кинематика.
Равномерное и равнопеременное движения.
Основные понятия: вектор перемещения, траектория, путь, координата, скорость, вектор скорости, мгновенная скорость, проекция вектора скорости, средняя (путевая) скорость, ускорение, вектор ускорения, мгновенное ускорение, проекция вектора ускорения, виды движения (прямолинейное, криволинейное, равномерное, ускоренное, замедленное, равнопеременное, поступательное, вращательное, плоскопараллельное).
Основные формулы кинематики:
;
;
; 
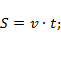
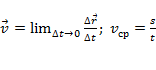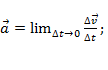
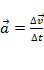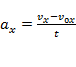(при равнопеременном движении);
.
.
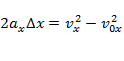Равнопеременное прямолинейное движение.
Формулы для вычисления пройденного пути:
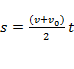(формула без ускорения);
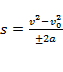(формула без времени);
.
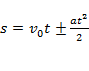Перемещение за n-ю секунду:
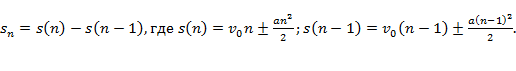
Связь координаты, скорости и ускорения: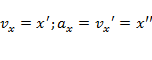 
.
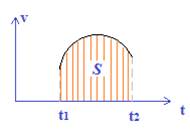Экзаменуемый должен уметь строить и анализировать графики зависимостей 
, уметь находить пройденный путь по графикам 
и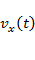 
, строить графики по таблицам. Путь, пройденный телом при любом движении, численно равен площади под графиком зависимости скорости от времени на заданном промежутке времени.
Свободное падение.
Основные понятия: ускорение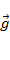 
(модуль и направление), независимость ускорения свободного падения от массы тела, основные формулы и графики при движении вверх и вниз.
Уравнения координаты и проекции скорости:
; 
; 
.
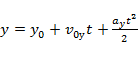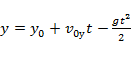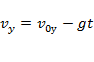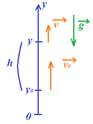Уравнения координаты и проекции скорости:
-при движении вверх (равнозамедленном):
; 
.
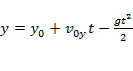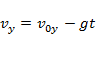- при движении вниз (равноускоренном):
; 
(
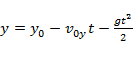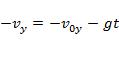Время свободного падения на землю без начальной скорости:
|
|
|
.
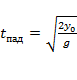Перемещение, высота:
; 
; 
.
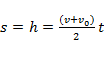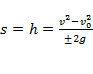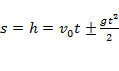Горизонтальный бросок: движение по 2 осям, формулы и графики, направление вектора скорости, разложение вектора скорости по 2 составляющим.
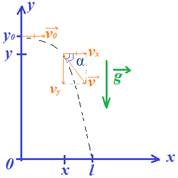Основные формулы:
; 
; 
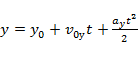проекции начальной скорости: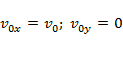 
проекции скорости в любой момент времени:
;
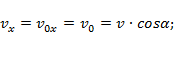
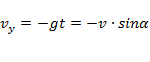модуль мгновенной скорости: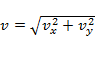 
;
угол наклона вектора скорости к горизонту: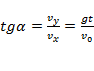 
;
горизонтальное смещение: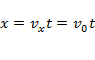 
;
время падения на землю: ;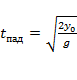
начальная высота: 
;
мгновенная высота: 
;
дальность полёта: 
уравнение траектории полёта: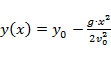 
.
Движение тела, брошенного под углом к горизонту: движение по 2 осям (в проекции на ось 0x – равномерное движение, в проекции на ось 0y – движение с постоянным ускорением), направление вектора скорости, разложение вектора скорости по 2 составляющим.
Основные формулы:
проекции начальной скорости:
;
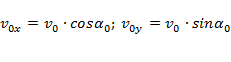проекции мгновенной скорости:
;
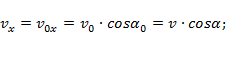
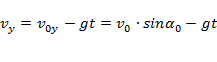модуль мгновенной скорости: ;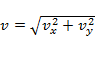
скорость в верхней точке траектории: 
;
угол наклона вектора скорости к горизонту:
;
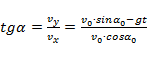горизонтальное смещение: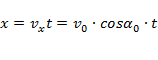 
;
уравнение координаты y (мгновенная высота): ;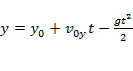
;
время подъёма (спуска):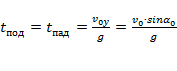 
;
время полёта: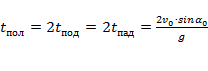 
;
наибольшая высота подъёма: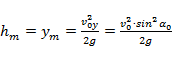 
;
дальность полёта: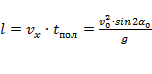 
;
уравнение траектории полёта: 
.
Отработать построение и анализ графиков зависимостей:
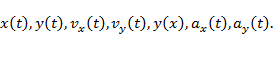
Равномерное движение по окружности.
Основные понятия: направление и модуль вектора линейной скорости, направление и модуль вектора центростремительного ускорения, угол поворота, длина дуги, угловая скорость, период и частота вращения, число оборотов.
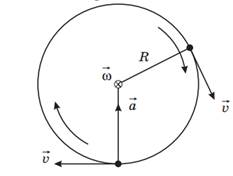
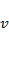– линейная скорость точки, 
;
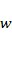– угловая скорость вращения, 
;
- угол поворота радиуса-вектора точки, движущейся по окружности,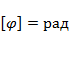 
;
R – радиус вращения,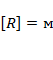 
;
T – период вращения,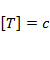 
;
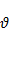– частота вращения, 
;
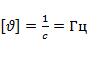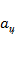- центростремительное (нормальное) ускорение, 
;
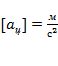S – путь, равный длине дуги окружности,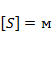 
;
N – число оборотов.
Основные формулы:
;
; 
; 
;
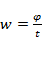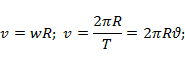
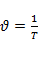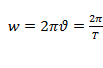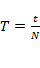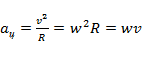
4. Относительность движения: система отсчёта (подвижная и неподвижная), абсолютная, относительная и переносная скорости, преобразования Галилея для скоростей и ускорений, принцип относительности Галилея.
|
|
|
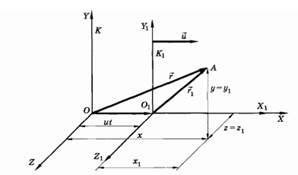Преобразования Галилея.
Система отсчёта K1 движется со скоростью 
относительно системы отсчёта K так, чтооси X,Y,Z и X1,Y1,Z1 остаются параллельными.
1) Преобразование координат: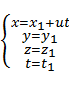 
2) Закон сложения скоростей:
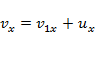или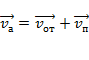 
– абсолютная скорость – скорость тела в неподвижной системе отсчёта;
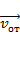– относительная скорость – скорость тела в подвижной системе отсчёта;
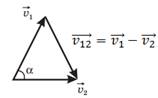
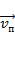– переносная скорость – скорость подвижной системы отсчёта относительно неподвижной.
Скорость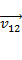 
первого тела, движущегося со скоростью 
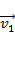, относительно второго тела, движущегося со скоростью 
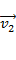, определяется формулой: 
.
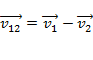3) Преобразование ускорений (система отсчёта K1 движется со ускорением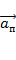 
относительно системы отсчёта K, не вращаясь, так, чтооси X,Y,Z и X1,Y1,Z1 остаются параллельными):
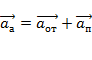
Если системы отсчёта K1 движется равномерно и прямолинейно относительно системы отсчёта K, то есть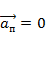 
, то ускорение одинаково, или абсолютно.
4) Принцип относительности Галилея: все механические явления в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
Динамика.
Основные понятия: 3 закона механики Ньютона, инерциальные и неинерциальные системы отсчёта (примеры), инерция, 4 типа фундаментальных взаимодействий, силы (сила тяжести, сила реакции опоры, сила упругости, сила натяжения нити, сила трения), вес тела, невесомость, масса тела (инертная и гравитационная), неподвижный и подвижный блоки, движение со связями, закон всемирного тяготения, гравитационная постоянная, первая и вторая космические скорости, зависимость ускорения свободного падения от высоты над планетой.
1. Первый закон Ньютона: существуют системы отсчёта, называемые инерциальными, в которых тела движутся равномерно и прямолинейно или покоятся, если на них не действуют другие тела.
Если относительно какой-либо системы отсчёта тело движется с ускорением, не вызванным действием на него других тел, то такую систему называют неинерциальной.
|
|
|
Любое тело, движущееся равномерно и прямолинейно или покоящееся, можно считать инерциальной системой отсчёта. Тело, движущееся равномерно по окружности, является неинерциальной системой отсчёта.
Любое тело, движущееся с ускорением в инерциальной системе отсчёта, является неинерциальной системой отсчёта.
Инерция – движение, при котором тело сохраняет свою скорость.
Масса тела.
Величину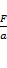 
, равную отношению модуля силы к модулю ускорения тела, называют инертной массой 
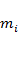тела.
Масса является мерой инертности тела. Инертностью называется свойство тела сохранять свою скорость неизменной (в инерциальной системе отсчёта), когда внешние воздействия отсутствуют или компенсируют друг друга. При наличии внешних воздействий инертность тела проявляется в том, что его скорость меняется не мгновенно, а постепенно, и тем медленнее, чем больше инертность тела, то есть его масса.
Массы тел также являются причиной их гравитационного притяжения друг к другу (об этом подробнее в теме “закон всемирного тяготения”).
Массу, определяющую способность тел притягиваться друг к другу, называют гравитационной массой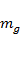 
.
Из многочисленных опытов механики следует, что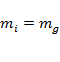 
.
Таким образом, масса тела – это количественная мера его инертных и гравитационных свойств.
Масса служит мерой содержащегося в теле вещества. Плотностью однородного тела называется отношение массы тела к его объёму:
, 
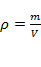3. Второй закон Ньютона: произведение массы тела на вектор ускорения есть равнодействующая всех сил, приложенных к телу:
,
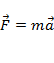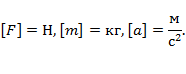
Справедливы следующие утверждения:
1. 
, где a — модуль ускорения, F — модуль равнодействующей силы.
2. Вектор ускорения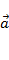 
сонаправлен с вектором равнодействующей силы 
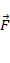, так как масса тела положительна.
Третий закон Ньютона: два тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Эти силы имеют одну и ту же физическую природу и направлены вдоль прямой, соединяющей их точки приложения.
.
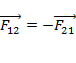Вес тела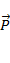 
и сила реакции опоры 
являются примерами сил действия и противодействия, связанных третьим законом Ньютона:
|
|
|
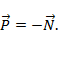
Силы. Виды сил.
Cила – количественная мера взаимодействия тел.
Фундаментальные взаимодействия определяют 4 вида сил в природе:
1) электромагнитные: сила трения, сила упругости, сила реакции опоры;
2) гравитационные: сила тяжести, сила тяготения;
3) ядерные силы (силы сильного взаимодействия);
4) силы слабого взаимодействия (удерживают элементарные частицы от распада).
Сила тяжести – сила, действующая на тело со стороны Земли. Эта сила приложена в центре тяжести тела.
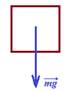
Сила реакции опоры, сила нормального давления, вес тела.
1) – сила реакции опоры – сила, с которой опора действует на тело.
2) 
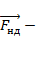сила нормального давления – сила, с которой тело давит на опору.
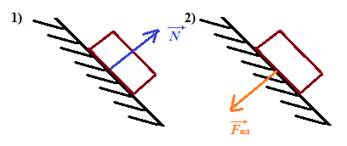
Обе силы перпендикулярны поверхности соприкосновения тел, равны по модули и противоположны по направлению: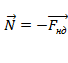 
, 
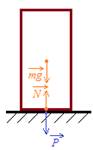3) Вес тела 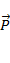- сила, с которой тело действует на опору или подвес. Из определения вес тела и сила нормального давления понятия равнозначные. Вес тела равен по модулю силе реакции опоры и противоположен ей по направлению: 
, 
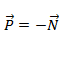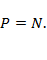На рисунке изображены силы тяжести, реакции опоры и вес тела. Силы тяжести и реакции опоры действуют на тело, сила реакции опоры действует на опору.
Состояние, при котором вес тела равен нулю, называется состоянием невесомости. В таком состоянии тело не давит на опору и не растягивает подвес. Свободное падение тела является примером невесомости.
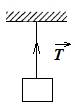
Сила натяжения нити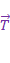 
– сила, с которой нить (подвес) действует на тело. Эта сила направлена по нити. Если тела связаны невесомой нитью, то натянутая нить действует с одинаковыми силами как на одно, так и на другое тело.
Сила трения – сила сопротивления, возникающая при относительном перемещении прижатых друг к другу тел. Эта сила направлена по касательной к поверхности соприкосновения тел и противоположно направлению перемещения данного тела.
1) Случай подвижного тела – возникает cила трения скольжения:
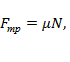
где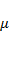 
– коэффициент трения скольжения (
).
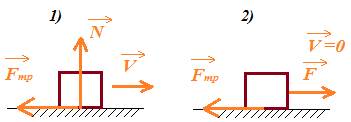
2) Случай неподвижного тела – возникает cила трения покоя:
.
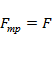Сила трения не зависит от площади соприкосновения поверхностей, а определяется коэффициентом трения поверхностей и модулем силы реакции опоры.
Сила упругости – это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:
1) действует между соседними слоями деформированного тела и приложена к каждому слою;
2) действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры).
|
|
|
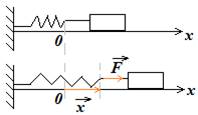
Закон Гука. Модуль силы упругости прямо пропорционален величине деформации. В частности, для пружины, сжатой или растянутой на величину x, сила упругости даётся формулой:
F = kx,
где k — коэффициент жёсткости пружины (жёсткость).
Коэффициент жёсткости k зависит не только от материала пружины, но также от её формы и размеров.
Закон Гука в векторной форме:
.
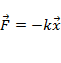Знак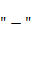 
показывает, что сила упругости направлена в противоположную сторону деформации.
Закон Гука справедлив только при малых деформациях.
Динамометр – прибор для измерения силы. Использование динамометра основано на том факте, что сила упругости пружины в определённых пределах прямо пропорциональна её деформации. По длине растянутой пружины можно судить о значении приложенной силы.
При параллельном соединении пружин жесткость системы равна: 
.
При последовательном соединении пружин жесткость системы равна: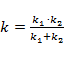 
.
Типовые задачи
1) Тело массой 100 г движется по шероховатой горизонтальной поверхности под действием силы F=2 Н, направленной под углом 300 к горизонтали. Определите ускорение тела. Коэффициент трения поверхности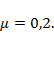 
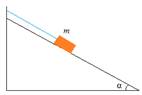
2) Тело массой m скользит без начальной скорости вниз по наклонной плоскости с углом наклона α. Определите ускорение тела в случае: а) трение о плоскость отсутствует; б) коэффициент трения тела о плоскость равен 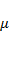. При каком коэффициенте трения ещё возможно скольжение?
3) Тело массой 1 кг лежит на горизонтальной поверхности. К нему в горизонтальном направлении прикладывают силу F. Коэффициент трения тела о плоскость равен 0,4. Определить ускорение тела и величину силы трения, если: а) F =5 Н; б) F =3 Н.
4) Верёвка удерживает тело массой m на гладкой наклонной плоскости с углом наклона α. Определите силу натяжения нити.
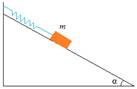
5) Пружина с жёсткостью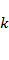 
удерживает тело массой m на гладкой наклонной плоскости с углом наклона α. На какую величину растянута пружина?
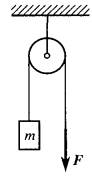6) К одному концу верёвки, перекинутой через блок, подвешен груз массы m =10 кг. С какой силой F нужно тянуть вниз за другой конец верёвки, чтобы груз поднимался с ускорением a =1 м/с2 ?
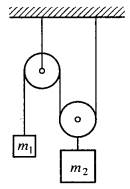7) Найти силу натяжения нити в устройстве, изображённом на рисунке, если массы тел 
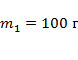и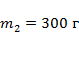 
.
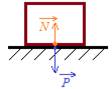
8) В покоящемся лифте лежит брусок массой m. Каким будет вес бруска при движении лифта:
а) вверх со скоростью v, вниз со скоростью v;
б) вверх ускоренно с ускорением a<g;
в) вниз ускоренно с ускорением a<g;
г) вверх замедленно с ускорением a<g;
д) вниз замедленно с ускорением a<g?
|
|
|
