Расчет ребристой предварительно напряженной плиты

РЕБРИСТЫЕ ПЛИТЫ

СБОРНЫХ ЖЕЛЕЗОБЕТОННЫХ ПЕРЕКРЫТИЙ

 

Методические указания к курсовому проекту по дисциплине

«Железобетонные и каменные конструкции»

для студентов всех форм обучения и МИППС направления

270800.62Строительство

 

 

Краснодар

Составители: канд. техн. наук, доц. М.А. Тамов

канд. пед. наук, доц. Е.Н. Карпанина

 

УДК 624.012.35:624.072.23.(07)

 

Ребристые плиты сборных железобетонных перекрытий: Методические указания к курсовому проекту по дисциплине «Железобетонные и каменные конструкции» для студентов всех форм обучения и МИППС направления 270800.62 Строительство/Сост.: М.А. Тамов, Е.Н. Карпанина; Кубан. гос. технол. ун-т. Каф. строительных конструкций. – Краснодар: Изд.КубГТУ, 2015.- 23с.

 

 

Изложены общие положения расчета и проектирования ребристой предварительно напряженной плиты по двум группам предельных состояний.

 

Ил. 12. Табл. 11. Библиогр.: 14 назв.

 

Печатается по решению методического совета ФГБОУ ВПО «Кубанский государственный технологический университет»

 

 

Рецензенты: канд. техн. наук, доц. кафедры СК КубГТУ

В.А. Гуминский;

начальник архитектурно-строительного отдела

ОАО «Кубаньводпроект» К.Ю. Деркач

 

©КубГТУ,2015

Общие указания по проектированию

 

Приступая к расчету плиты перекрытия, нужно иметь исходные данные для расчета, полученные в процессе работы над компоновкой конструктивной схемы перекрытия. Должны быть установлены размеры сетки колонн, расположение ригелей, назначен тип, ширина и длина плит, произведена раскладка плит с составлением соответствующей схемы.

Принятый тип плиты перекрытия и схема раскладки утверждается руководителем курсового проекта на стадии компоновки перекрытия.

Дополнительно к имеющимся данным, а также данным, указанным в задании, устанавливаются: высота сечения элемента, толщина полки плиты, размеры сечения ребер, расчетный пролет плиты; конструкция пола перекрытия; производится подсчет нагрузок.

Рассмотрим более подробно каждое из этих положений.

Высоту сечения предварительно напряженных ребристых плит можно предварительно назначить равной:

 

h = l₀ /20

 

В промышленных зданиях номинальная ширина плит перекрытий 1500, 3000 мм. Доборные элементы имеют 1000, 750 и 500 мм.

Расчетный пролет плиты принимается равным расстоянию между осями опор, его величина зависит от условий опирания плиты на ригели.

При опирании плиты на ригель по верху расчетный пролет (рис.1):

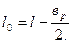(1)

при опирании плиты на боковые полки ригелей

 

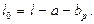
Рисунок 1

Тип и состав конструктивных элементов пола зависит от технологических требований производства, величины и характера временных нагрузок и других.

Подсчет нагрузок лучше выполнять в табличной форме (см. табл. 1) отдельно подсчитываются нормативные и расчетные нагрузки на 1 м² перекрытия.

 

Расчет ребристой предварительно напряженной плиты

2.1 Данные для расчета

 

Для примера расчета принята ребристая плита с номинальной шириной b = 1200 мм идлиной l = 6000 мм.

Материалы для плиты:

Бетон класса В25. Призменная прочность нормативная R_bn = R_b,ser = 18,5 МПа; расчетная R_b = 14,5 МПа; коэффициент условий работы бетона γ_b1 = 0,9; нормативное сопротивление при растяжении R_btn = R_bt,ser = 1,55 МПа; расчетное R_bt = 1,05 МПа; начальный модуль упругости бетона Е_b = 30000 МПа.

Напрягаемая арматура в продольных ребрах класса А800. Нормативное сопротивление R_sn = R_s,ser =800 МПа; расчетное сопротивление растяжению R_s = 695 МПа; модуль упругости E_s = 200000 МПа.

Ненапрягаемая арматура:

Класса В500 в полке плиты в виде сварных сеток. Нормативное сопротивление R_sn = R_s,ser =500 МПа; расчетное сопротивление растяжению R_s = 415 МПа; R_sw = 300 МПа

Класса А300 в продольных и поперечных ребрах в виде продольной рабочей арматуры в сварных каркасах. Нормативное сопротивление R_sn = R_s,ser =300 МПа; расчетное сопротивление растяжению R_s = 270 МПа;

Технология изготовления плиты - агрегатно-поточная с пропариванием.

Рассчитываемая плита будет работать в закрытом помещении при влажности воздуха окружающей среды выше 40%.

Требования к расчету по второй группе предельных состояний:

- из условия обеспечения сохранности арматуры и условия ограничения проницаемости конструкции допускается ограниченное по ширине непродолжительное a_crc = 0,3 мм и продолжительное a_crc = 0,2 мм раскрытие трещин;

- предельно допустимый прогиб плиты при ее пролете l = 6 м равен / f / = 2,0 см.

 

 

2.2 Расчетный пролет и нагрузки

Нормативные и расчетные нагрузи на 1 м² перекрытия приведены в табл. 1.

Для установления расчетного пролета плиты предварительно задаемся размерами сечения ригеля: 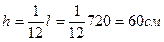/кратно 5 см при h ≤ 60 см; кратно 10 см при h ³ 60 см /, b = /0,35-0,4/ h = 0,4×60 = 25 см.

Расчетный пролет плиты при опирании на ригель поверху:

 

 

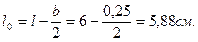
Т а б л и ц а1

№ п/п	Наименование нагрузки	Нормативная нагрузка, Па	Коэф. надёжности по нагрузке γf	Расчётная нагрузка, Па
	Постоянная Собственный вес ребристой плиты бетонный пол из плиток, δ=25 мм () Цементный раствор, δ=15 мм ()     ИТОГО:		1,1     1,1   1.3
	-
	Временная полезная (см. задание на КП) В том числе: Длительная кратковременная		1,2   1,2 1,2
	Полная нагрузка В том числе: Постоянная и длительная кратковременная		-   -   -

Расчетная нагрузка на 1 м длины при ширине плиты 1,2 м с учетом коэффициента надежности по назначению здания / g_n = 0,95/:

 

постоянная g = 3667×1,2×0,95 = 4180 Н/м;

 

полная g+p = /3667+7200/×1,2×0,95 = 13040 H/м.

 

Нормативная нагрузка на 1 м длины:

 

постоянная g = 3290×1,2×0,95 = 3750 H/м

 

полная g + V = /3290+6000/×1,2×0,95 = 10590 H/м,

 

в том числе постоянная и длительная полезная:

 

/3290+4500/×1,2×0,95 = 8880 H/м.

 

2.3 Усилия от расчетных и нормативных нагрузок

 

От полной расчетной нагрузки: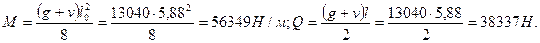

От полной нормативной нагрузки:

;

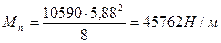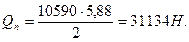
От нормативной постоянной и длительной:

;

 

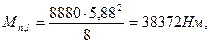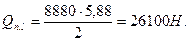
2.4 Компоновка поперечного сечения плиты

 

Принимаем плиту со следующими параметрами (рис. 2): высота сечения предварительно-напряженной плиты h = l₀ /20 = 588/20 = 30 cм, рабочая высота сечения h₀ = h-a = 30-3 = 27 см, ширина плиты по низу b_g = b_n -1 = 120- 1 = 119 cм, ширина плиты по верху b'_f = b_n - 2×2,5 = 120-5 = 115 см, толщина полки h_f = 5 см, ширина продольных ребер по низу – 7 см.

Приведенное поперечное сечение (рис. 2б) плиты имеет тавровую форму со следующими параметрами: b'_f = 115 cм, при условии h'₁/h = 5/30 = 0,167 > 0,1 в расчет вводится вся ширина полки b_f = 115 см, расчетная ширина ребра принимается как среднее арифметическое ширины верха и низа ребра: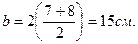

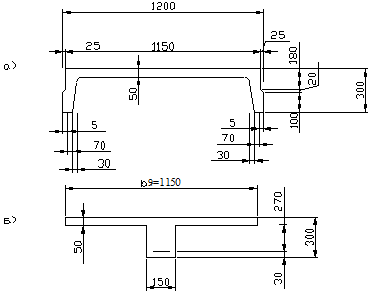
Рисунок 2 - Ребристая плита:

а - проектное сечение; б - приведенное сечение

 

2.5 Расчет полки на местный изгиб

 

В отсутствие поперечных промежуточных ребер полка плиты рассматривается как балочная плита, опертая на два продольных ребра плиты.

Расчетный пролет при ширине ребер вверху 8 см составит

l₀ = 115-2×8 = = 99 см,

где 8 см – ширина продольного ребра вверху.

 

Расчетная нагрузка на 1 м² полки:

q = g + g₁ + v = (917 + 1375 + 7200)×0,95 = 9017 Н/м², где g и v принимаются по табл. 1.;

g₁ = h'_f×1×1×g×g_f = 0,05×1×1×25000×1,1 = 1375 Н/м² – нагрузка от собственной массы полки.

Изгибающий момент для полосы шириной 1 м определяется с учетом пластичной заделки в ребрах

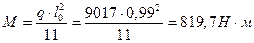
Рабочая высота сечения

h₀ = 5-1,5 = 3,5 см.

Арматура & 3 В500 с R_s = 415 МПа.

Рассчитываем площадь сечения рабочей арматуры

А_s = 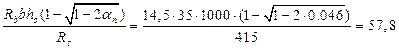мм²

где a_n=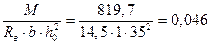

Принимаем сетку с поперечной рабочей арматурой Ø3 В500 с шагом 100 мм и общей площадью А_s=63,6 мм² на рассчитанную полосу шириной 1 м.

2.6 Расчет прочности сечений, нормальных к продольной оси плиты

Расчетныйизгибающий момент от полной нагрузки М = 5634900 Нсм. Расчетное сечение тавровое, поэтому необходима проверка положения нейтральной линии. Если условие 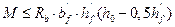выполняется, то нейтральная линия проходит в полке

 

 

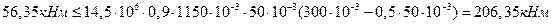
Условие выполняется, поэтому расчет производим как для прямоугольного сечения с шириной b=1150 мм.

 

 

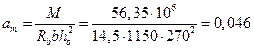
По табл. 3.1(2) при классе арматуры А800 и σ_sp/R_s = 0,6 находим ξ_R = 0,41.

Тогда a_R = ξ_R(1- ξ_R/2) = 0,41(1-0,41/2) = 0,326 > а_m= 0,046, т.е. сжатой арматуры не требуется.

Определяем

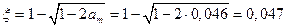
и коэффициент γ_s3 согласно п.3.9(2).

Так как ξ/ξ_R = 0,047/0,41=0,115 < 0,6 принимаем γ_s3=1,1.

Тогда при A_s = 0

 

 

Принимаем 2Æ14 А800 с А_sp = 308 мм².

 

2.7 Определение усилий предварительного обжатия

 

Геометрические характеристики сечения:

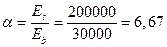
Площадь бетона A=1150·50+150·250= 95000 мм²;

Приведенная площадь A_red = A + aA_sp= 95000 + 6,67·308 = 97054,36 мм²;

Статический момент сечения бетона относительно нижней грани:

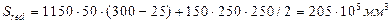
Расстояние от нижней грани до центра тяжести всего сечения:

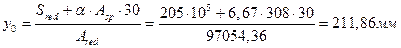
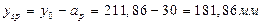
Момент инерции приведенного сечения:

 

 

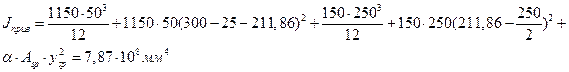
Принимаем σ_sp в пределах:

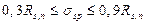
Максимально допустимое значение σ_sp без учета потерь равно

 

σ_sp = 0,9 R_s,_n = 0,9·800 = 720 МПа.

Первые потери:

Потери от релаксации напряжений в арматуре равны

 

 

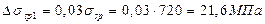
По агрегатно-поточной технологии изделие при пропаривании нагревается вместе с формой и упорами, поэтому температурный перепад между ними равен нулю и, следовательно, Δσ_sp2 = 0.

Потери от деформации формы Δσ_sp3 и анкеров Δσ_sp4 при электротермическом натяжении арматуры равны нулю.

Таким образом, сумма первых потерь равна

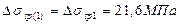
Усилие обжатия с учетом первых потерь

 

P ₍₁₎ = A_sp (σ_sp - Δ σ_{sp (1)})=308(720-21,6)=215,1кН

 

В связи с отсутствием в верхней зоне напрягаемой арматуры (т.е. при A'_sp = 0) имеем

 

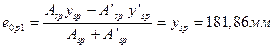
Предварительные напряжения в бетоне σ_bp при передаче усилия предварительного обжатия P₍₁₎ не должны превышать0,9R_bp, если напряжения уменьшаются или не изменяются при действии внешних нагрузок.

Принимаем, что момент от собственного веса равен нулю

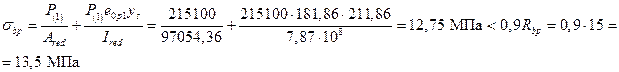
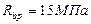(см. п.2.3 [2])

 

Определяем вторые потери напряжений согласно пп.2.31и 2.32[2].

 

Потери от усадки равны Δσ_sp5 = ε_b,shE_s= 0,0002·2·10⁵ = 40 МПа.

 

Потери от ползучести определяем, принимая значения φ_b,сr и Е_b по классу бетона В25 (согласно табл.2.6[2] φ_b,сr = 2,5)

коэффициент армирования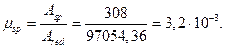

Определяем нагрузку от массы плиты

 

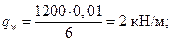
и момент от этой нагрузки в середине пролета

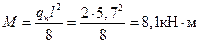
(здесь l = 5,7 м – расстояние между прокладками при хранении плиты);

Тогда определим напряжение бетона на уровне арматуры S при y_sp =181,86мм:

 

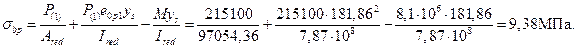
Потери от ползучести:

 

 

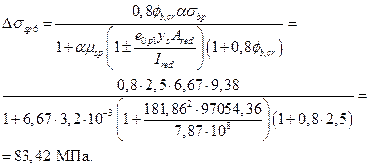
Вторые потери для арматуры равны

Δσ_sp(2) = Δσ_sp5 + Δσ_sp6 = 40 + 83,42 = 123,42 МПа.

 

Суммарная величина потерь напряжения

Δσ_sp(1) + Δσ_sp(2) = 21,6 + 123,42 = 145,02 МПа > 100 МПа,

 

следовательно, требование п.2.36[2] выполнено и потери не увеличиваем.

 

Напряжение σ_sp2 с учетом всех потерь равно

 

σ_sp2 = 720 -145,02 = 574,98 МПа.

 

Определяем усилие обжатия с учетом всех потерь напряжений Р.

 

Р= σ_sp2A_sp - σ_sA_s = 574,98·308 = 177093 Н=177,09кН;

 

Эксцентриситет усилия Р равен

 

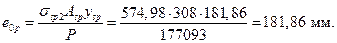
2.8 Расчет прочности по наклонным сечениям

 

Расчет на действие поперечных сил

Прочность бетонной полосы проверяем из условия ,

где Q – поперечная сила в нормальном сечении, принимаемом на расстоянии от опоры не менее

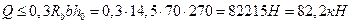
Так как 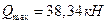, то условие выполнено.

Определяем необходимость постановки поперечной арматуры по выполнению условия 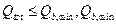. Для этого находим 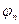по формуле:

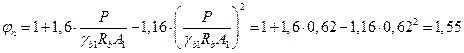
Здесь

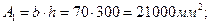
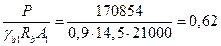
Таким образом,

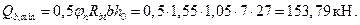
Так как 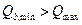, то постановка поперечной арматуры не требуется.

Принимаем четыре каркаса с арматурой ∅4В500 и шагом поперечных стержней 100 мм 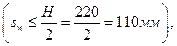тогда

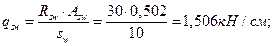
По формуле поперечная сила, воспринимаемая хомутами,

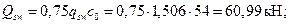
где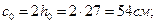

Поперечную силу, воспринимаемую бетоном, находим по формуле:

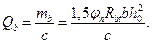
Для этого невыгоднейшее значение с при равномерной нагрузке рассчитаем по следующей формуле

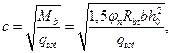
где ;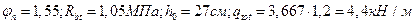

Отсюда

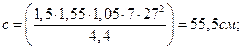
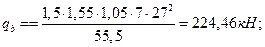
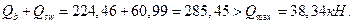
Условие прочности наклонного сечения по поперечной силе выполнено.

Расчет на действие изгибающего момента

Длина зоны передачи напряжений определяется по формуле:

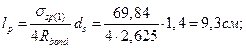
где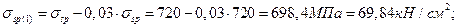

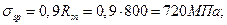
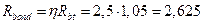(η=2,5 для горячекатаной и термически упрочненной арматуры класса А);

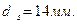
Расстояние от торца панели до начала зоны передачи напряжений

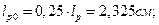
Проверяем выполнение условия прочности

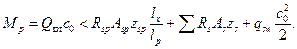
Момент 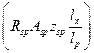, воспринимаемый напрягаемой арматурой, учитывается, так как

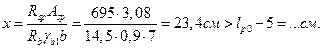
Рассчитываем этот момент

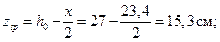
Длина площадки опирания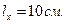

Отсюда

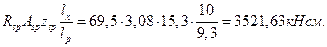
Определяем момент 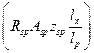, воспринимаемой продольными нижними проволоками каркасов 4∅4В500, (A_s = 0,502 см²) ;

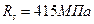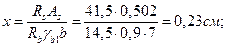
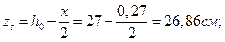
Отсюда

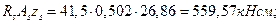
Вычисляем момент 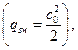воспринимаемой поперечной арматурой:

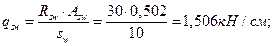
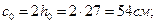
Отсюда

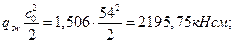
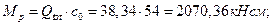
Таким образом,

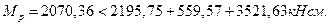
Следовательно, несущая способность обеспеченна.

 

2.9 Расчет предварительно напряженной плиты по предельным состояниям 2-й группы.

 

2.9.1 Расчет по раскрытию трещин

 

Момент образования трещин предварительно напряженных изгибаемых элементов в стадии эксплуатации:

 

 

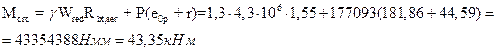
М_tot=М_n= 45,76 кНм, 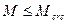, т.е. трещины в растянутой зоне образуются. Требуется расчёт по раскрытию трещин.

 

Расчет по раскрытию трещин производят из условия

a_crc ≤ a_crc,ult

Предельно допустимая ширина раскрытия трещин при продолжительном раскрытии трещин а_crc,ult=0,2мм. Предельно допустимая ширина раскрытия трещин при непродолжительном раскрытии трещин а_crc,ult=0,3мм.

Ширина раскрытия нормальных трещин определяется по формуле (п.4.8 [2]):

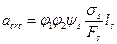
φ₁ - коэффициент, учитывающий продолжительность действия нагрузки и принимаемый равным:

1,0 - при непродолжительном действии нагрузки;

1,4 - при продолжительном действии нагрузки;

φ₂ - коэффициент, учитывающий профиль арматуры и принимаемый равным:

0,5 - для арматуры периодического профиля и канатной;

0,8 - для гладкой арматуры (класса А240);

ψ_s - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами; допускается принимать ψ_s = 1; если при этом условие a_crc ≤ a_crc,ult не удовлетворяется, значение ψ_s следует определять по формуле

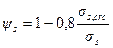
где σ_s,crc - приращение напряжений в растянутой арматуре в сечении с трещиной сразу после образования нормальных трещин, т.е. при М = M_crc.

Приращение напряжений в растянутой арматуре при действии постоянных и длительных нагрузок

 

 

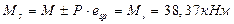
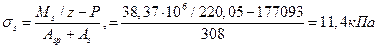
Плечо внутренней пары сил 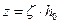, где 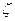зависит от:

1)

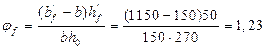
2)

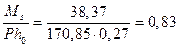
3) a_{s 1} = 300/ R_b,ser (для канатной арматуры - a_{s 1}= 270/ R_bser)

 

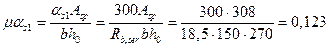
Определяем 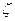по табл. 4.2 [2].

,

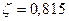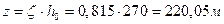
При действии всех нагрузок

 

 

,

 

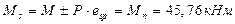
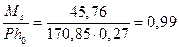
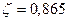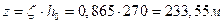
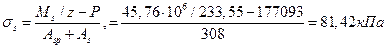
Базовое расстояние между трещинами ():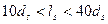

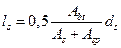
А_bt - площадь сечения растянутого бетона.

 

Высота растянутой зоны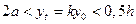

к - поправочный коэффициент, учитывающий неупругие деформации растянутого бетона и равный: для прямоугольных сечении и тавровых с полкой в сжатой зоне - 0,9; для двутавровых (коробчатых) сечений и тавровых с полкой в растянутой зоне - 0,95.

 

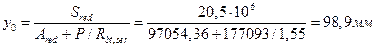
Тогда получим:

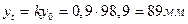, т.к. ,

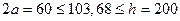то

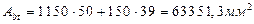
Отсюда

,

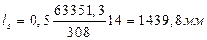т.к.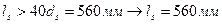

a_crc1 - ширина раскрытия трещин, определяемая при φ₁ = 1,4 и при действии постоянных и длительных нагрузок (т. е. при М = M_l);

a_crc2 - то же, при φ₁ = 1,0 и действии всех нагрузок (т.е. при М = M_n);

a_crc3 - то же, при φ₁ = 1,0 и действии постоянных и длительных нагрузок (т.е. при М = M_l)

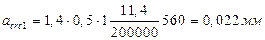
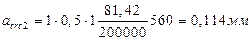
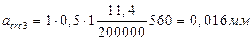
Продолжительное раскрытие трещин: a_crc = a_{crc 1}=0,022<0,2 мм

Непродолжительное раскрытие:

→ трещины раскрываются в пределах допустимого.

 

2.9.2 Расчет плиты по деформациям/определение прогиба

 

Расчет производят из условия: f ≤ f_ult, f_ult =l/250

Для элементов постоянного сечения прогиб допускается определять по формуле

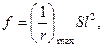
S=5/48 - коэффициент, принимаемый по табл.4.3 [2]

Для участков с трещинами прогиб определяют по формуле:

Найдем кривизну от непродолжительного действия всех нагрузок:

при непродолжительном действии всех нагрузок

при продолжительном действии всех нагрузок

Определяем вспомогательные значения для нахождения

,

По таблице 4.5 [2] находим

Отсюда

Найдем - кривизна от непродолжительного действия постоянных и длительных нагрузок:

,

По таблице 4.5 находим

Отсюда

Найдем кривизна от продолжительного действия постоянных и длительных нагрузок:

,

По таблице 4.5 находим

Отсюда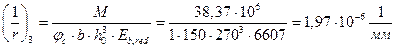

Тогда

Вычисляем прогиб плиты

< мм→ прогиб не превышает предельно допустимый.

 

2.10 Расчет плиты на усилия, возникающие при изготовлении,

транспортировании и монтаже

 

За расчетное сечение принимаем сечение, расположенное на расстоянии 0,8 м от торца плиты.

 

Рисунок 3 - К расчету плиты в стадии изготовления, транспортирования и монтажа

 

Расчет ведем на совместное действие внецентренного сжатия N_tot и изгибающего момента от собственной массы:

q_с.в. = 0,14×0,25 + 1,16×0,05 ´ 25000×1,1 = 2325 Н/м;

 

тогда М_с.в. = q_с.в.l²/2 = 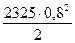= 744 Нм.

Определяем А₀

 

 

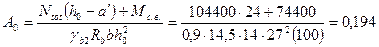
По табл. 111.1(2) находим h = 0,89, тогда

 

 

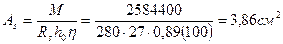
Следовательно, в верхней зоне должно быть не менее 2Æ16 A300 с A_s = 4,02 см².

 

 

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: