 |
Методика поэтапного расчёта поршневого шламового насоса
|
|
|
|
Приведённая методика расчёта поршневого шламового насоса является адаптацией под отечественные нормы и стандарты методики выбора насосов, предлагаемой фирмой Flygt. [4]
Этап 1. Необходимо определить плотность, удельную плотность шлама и удельную плотность твёрдых частиц.
Удельная масса – это плотность определённых материалов, нормированных плотностью воды.
Объемы шлама V (м3) при различной плотности определяются по следующей зависимости
, (2.1)
где Q – количество твердого в единице объема, т/м3; R – отношение массы жидкого к массе твердого, %; ρтв – плотность твердого, т/м3.
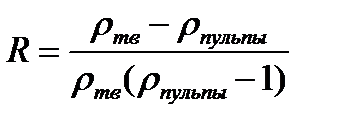, (2.2)
где ρпульпы – плотность пульпы, т/м3 (в данном за значение плотности пульпы применяем значение плотности шлама).
Этап 2. Требуется рассчитать критическую скорость.
В настоящее время одним из основных и наиболее разработанных вопросов гидравлического расчёта является определение критических скоростей.
Критерием для установления скорости потока служит критическая скорость vкр, т.е. наименьшая скорость, при которой шлам не скапливается в шламопроводе.
При определении скорости, напора или давления несущей среды первостепенное значение имеют крупность частиц и плотность перемещаемой гидросмеси. Размер частиц твердой фазы определяет условия их гидродинамического взаимодействия с потоком несущей жидкости. По преимущественному содержанию определенного класса частиц выделяют следующие виды гидросмесей [5]:
- коллоидные, содержащие частицы размерами до 1 мкм;
- структурные (гидрозоли), содержащие твердые частицы размерами от 1 до 50 мкм, получаемые диспергированием (для частиц структурных жидкостей гидродинамическое взаимодействие определяется в основном силами вязкости — законом Стокса);
|
|
|
- тонкодисперсные — с частицами размерами от 50 до 150 мкм, получаемые чаще всего измельчением (для тонкодисперсных гидросмесей — суспензий — взаимодействие частиц и жидкости определяется зависимостью гидравлического сопротивления от вязкости жидкости; это сопротивление тем больше, чем мельче частицы);
- грубодисперсные— с частицами размерами от 0,1—0,15 мм до 1,5—2 мм;
- неоднородные грубодисперсные — с частицами размерами более 1,5—2 мм (взаимодействие потока с частницами лежит в области квадратичных сопротивлений);
- полидисперсные — с частицами различной крупности.
Гранулометрический состав твёрдой фазы гидросмесей можно приближённо охарактеризовать среднеарифметической (средневзвешанной) крупностью частиц [6]:
, (2.3)
где 
– средняя крупность частиц из i – го интервала, 
– массовое процентное содержание частиц i – го интервала,
С позиций гидродинамики в структурных гидросмесях при насыщении жидкости твердыми веществами более 35 % вследствие малых размеров частиц и большой их концентрации основную роль в движении смеси играет твердая фаза.
В то же время в различных гидросмесях при концентрации до 25—35 % по объему основная роль в переносе твердого компонента принадлежит жидкости. Процессы в них носят гидродинамический характер, обусловленный скоростями и давлениями внутри жидкости и на границах соприкосновения жидкости с поверхностью трубопроводов.
Для определения критических скоростей движения шлама в шламопроводе предложено свыше десятка формул. В некоторых формулах критическая скорость vкр зависит от плотности пульпы, которая выражена в весовой консистенции по отношению веса воды или в объёмной консистенции, в других формулах вместо плотности пульпы употребляется удельный вес гидросмеси. Так же, в формулы входит весовая консистенция от веса гидромассы употребляется объёмная консистенция от объёма воды.
|
|
|
Аналитическая проверка, проведённая учёными, показывает большое расхождение в значениях критических скоростей и гидравлических уклонов по формулам, предложенным разными авторами.
Опыт гидравлического транспортирования шламов показывает, что наибольшая степень сходимости результатов расчёта критических скоростей с данными эксплуатации получается по формулам Всесоюзного научно-исследовательского института гидротехники им. Веденеева (ВНИИГ). [7,8]
Данные формулы определены для различных диапазонов средневзвешанного размера твёрдых частиц d ср, выраженного в миллиметрах.
1) для d ср ≤ 0,07 мм
, (2.4)
где 
– весовое содержание твёрдого в шламе, выраженное в процентах по отношению к весу воды; D – диаметр пульпопровода.
2) для 0,07 мм < d ср ≤ 0,15 мм
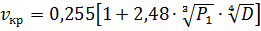, (2.5)
3) для 0,15 мм < d ср ≤ 0,4 мм
, (2.6)
4) для 0,4 мм < d ср ≤ 1,5 мм
, (2.7)
где d – средневзвешенный размер твёрдых частиц, выраженный в миллиметрах.
5) для d ср > 1,5 мм
. (2.8)
Для расчётов и построения графиков зависимостей между средневзвешенным размером твёрдых частиц, весовым содержанием твёрдого в шламе и диаметром трубопровода принимаем следующие наиболее распространённые на горно-добывающих предприятиях Южного Урала значения:
– диаметр трубопровода – согласно ГОСТ 9940-81 «Трубы бесшовные горячедеформированные из коррозионно-стойкой стали» принимаем диаметры трубопроводов: 76, 83, 89; 95; 102; 114; 121; 127; 133; 140; 146; 152; 159; 168; 180; 194; 219; 245; 273 и 325 метра. [9]
– средневзвешенный размер твёрдых частиц – от 0,02 до 2 мм;
– весовое содержание твёрдого в шламе – 60 %;
Как видно из формулы, для шлама с d ср ≤ 0,07 мм само значение d ср не влияет на значение критической скорости 
. Проведённый в среде MS Excel расчёт показал, что на значение влияют диаметр трубопровода D и весовое содержание твёрдого в шламе P1, но т.к. мы принимаем для расчёта весовое содержание твёрдого в шламе – 95%, то получили зависимость критической скорости от диаметра трубопровода D. Полученные расчётные данные приведены в таблице 2.1. Полученный график зависимости критической скорости от диаметра трубопровода D при d ср ≤ 0,07 мм показан на рисунке 11.
Таблица 2.1 – Расчётные данные для определения зависимости критической скорости при d ср ≤ 0,07 мм
|
|
|
| Значение P1, % | Значение D, м | Значение d, мм | Критическая скорость vкр, м/с |
| 0,076 | 0,02–0,07 | 1,521 | |
| 0,083 | 0,02–0,07 | 1,543 | |
| 0,089 | 0,02–0,07 | 1,561 | |
| 0,095 | 0,02–0,07 | 1,577 | |
| 0,102 | 0,02–0,07 | 1,596 | |
| 0,114 | 0,02–0,07 | 1,625 | |
| 0,121 | 0,02–0,07 | 1,641 | |
| 0,127 | 0,02–0,07 | 1,655 | |
| 0,133 | 0,02–0,07 | 1,667 | |
| 0,14 | 0,02–0,07 | 1,681 | |
| 0,146 | 0,02–0,07 | 1,693 | |
| 0,152 | 0,02–0,07 | 1,704 | |
| 0,159 | 0,02–0,07 | 1,717 | |
| 0,168 | 0,02–0,07 | 1,733 | |
| 0,18 | 0,02–0,07 | 1,753 | |
| 0,194 | 0,02–0,07 | 1,775 | |
| 0,219 | 0,02–0,07 | 1,811 | |
| 0,245 | 0,02–0,07 | 1,845 | |
| 0,273 | 0,02–0,07 | 1,879 | |
| 0,325 | 0,02–0,07 | 1,935 |
Рисунок 11– График зависимости критической скорости от диаметра трубопровода D при d ср ≤ 0,07 мм
Аналогичная ситуация наблюдается для шламов со значениями 0,07 мм < d ср ≤ 0,15 мм. Расчётные данные приведены в таблице 2.2. График зависимости критической скорости от диаметра трубопровода D при 0,07 мм < d ср ≤ 0,15 мм. показан на рисунке 12.
Таблица 2.2 – Расчётные данные для определения зависимости критической скорости при 0,07 мм < d ср ≤ 0,15 мм
| Значение P1, % | Значение D, м | Значение d, мм | Критическая скорость vкр, м/с |
| 0,076 | 0,083–0,15 | 1,770 | |
| 0,083 | 0,083–0,15 | 1,804 | |
| 0,089 | 0,083–0,15 | 1,831 | |
| 0,095 | 0,083–0,15 | 1,857 | |
| 0,102 | 0,083–0,15 | 1,886 | |
| 0,114 | 0,083–0,15 | 1,932 | |
| 0,121 | 0,083–0,15 | 1,957 | |
| 0,127 | 0,083–0,15 | 1,978 | |
| 0,133 | 0,083–0,15 | 1,998 | |
| 0,14 | 0,083–0,15 | 2,020 | |
| 0,146 | 0,083–0,15 | 2,039 | |
| 0,152 | 0,083–0,15 | 2,057 | |
| 0,159 | 0,083–0,15 | 2,077 | |
| 0,168 | 0,083–0,15 | 2,102 | |
| 0,18 | 0,083–0,15 | 2,135 | |
| 0,194 | 0,083–0,15 | 2,170 | |
| 0,219 | 0,083–0,15 | 2,229 | |
| 0,245 | 0,083–0,15 | 2,285 | |
| 0,273 | 0,083–0,15 | 2,341 | |
| 0,325 | 0,083–0,15 | 2,434 |
Рисунок 12 – График зависимости критической скорости от диаметра трубопровода D для 0,07 мм < d ср ≤ 0,15 мм
На данном графике видно, что изменяется форма кривой зависимости и увеличились значения критической скорости при стандартных значениях диаметра трубопровода D.
В формуле критической скорости для шламов со значениями 0,15 мм < d ср ≤ 0,4 мм наблюдается такое же отсутствие зависимости от величины d ср как и в двух предыдущих случаях. Расчётные данные приведены в таблице 2.3. График зависимости критической скорости от диаметра трубопровода D при 0,15 мм < d ср ≤ 0,4 мм. показан на рисунке 13.
|
|
|
Таблица 2.3 – Расчётные данные для определения зависимости критической скорости при 0,15 мм < d ср ≤ 0,4 мм
| Значение P1, % | Значение D, м | Значение d, мм | Критическая скорость vкр, м/с |
| 0,076 | 0,19–0,4 | 3,730 | |
| 0,083 | 0,19–0,4 | 3,781 | |
| 0,089 | 0,19–0,4 | 3,822 | |
| 0,095 | 0,19–0,4 | 3,861 | |
| 0,102 | 0,19–0,4 | 3,903 | |
| 0,114 | 0,19–0,4 | 3,970 | |
| 0,121 | 0,19–0,4 | 4,007 | |
| 0,127 | 0,19–0,4 | 4,037 | |
| 0,133 | 0,19–0,4 | 4,066 | |
| 0,14 | 0,19–0,4 | 4,098 | |
| 0,146 | 0,19–0,4 | 4,125 | |
| 0,152 | 0,19–0,4 | 4,151 | |
| 0,159 | 0,19–0,4 | 4,180 | |
| 0,168 | 0,19–0,4 | 4,216 | |
| 0,18 | 0,19–0,4 | 4,261 | |
| 0,194 | 0,19–0,4 | 4,311 | |
| 0,219 | 0,19–0,4 | 4,393 | |
| 0,245 | 0,19–0,4 | 4,470 | |
| 0,273 | 0,19–0,4 | 4,546 | |
| 0,325 | 0,19–0,4 | 4,671 |
Рисунок 13 – График зависимости критической скорости от диаметра трубопровода D при 0,15 мм < d ср ≤ 0,4 мм
В формуле для определения критической скорости появляется множитель, учитывающий средневзвешенный размер твёрдых частиц d ср. Вследствие этого, на графике зависимости критической скорости от диаметра трубопровода D для 0,4 мм < d ср ≤ 0,5 мм получается не одна кривая, указывающая значения критической скорости , а несколько, в зависимости от того, сколько значений из диапазона от 0,15 до 0,4 приняты для расчётов. В нашем случае принято 6 значений d ср: 0,58; 0,76; 0,94; 1,12; 1,3; 1,5, соответственно на графике получили 6 кривых значений критической скорости . Данный график представлен на рисунке 14, кривые критической скорости выделены красным цветом.
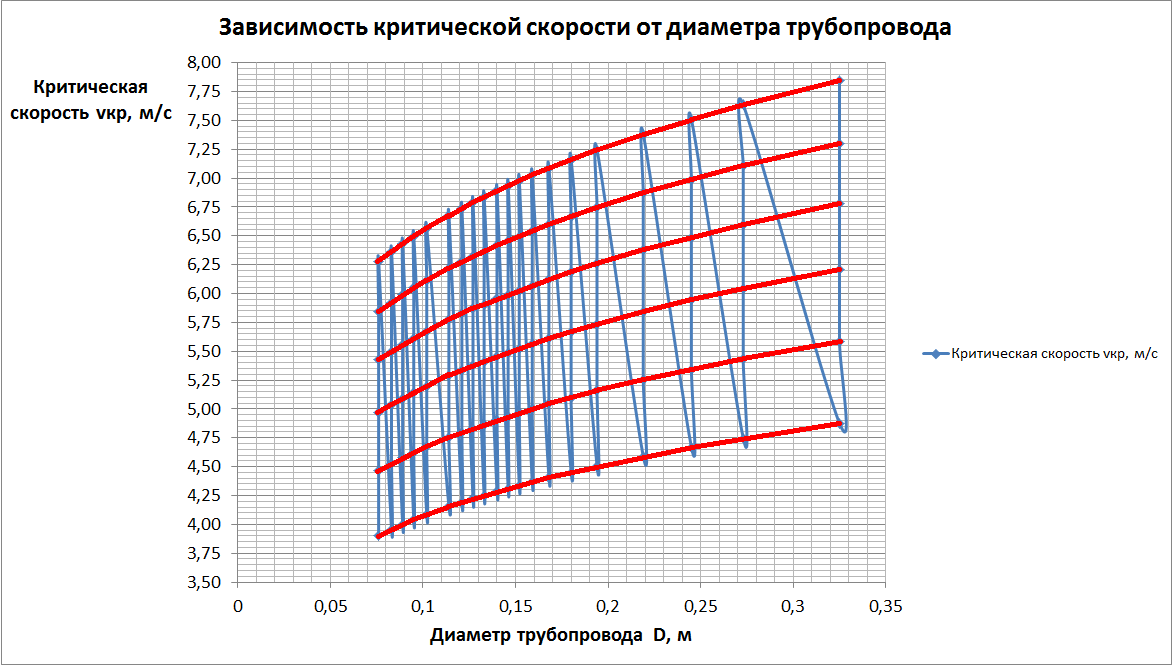
Рисунок 14 – График зависимости критической скорости от диаметра трубопровода D для 0,4 мм < d ср ≤ 0,15 мм
Аналогично формуле для определения критической скорости при значениях 0,4 мм < d ср ≤ 0,15 мм в формуле для определения критической скорости при значениях d ср > 1,5 мм появляется множитель, учитывающий значения средневзвешенный размер твёрдых частиц d ср. В этом случае на графике зависимости критической скорости от диаметра трубопровода D для d ср > 1,5 мм также появляются несколько кривых значений критической скорости .Для расчёта принято 6 значений d ср: 1,55; 1,6; 1,7; 1,8; 1,9; 2,0 мм. График представлен на рисунке 15, кривые критической скорости выделены красным цветом.
При расчёте критических скоростей 
и рассмотрении графиков было определено, что при средневзвешенном размере твёрдых частиц d ср от 0,02 мм до 1,5 мм критическая скорость достигла максимального значения 7,84 м/с, а при d ср> 1,5 мм всего 6,05 м/с. Таким образом, нельзя с уверенностью утверждать, что с увеличением средневзвешенного размера твёрдых частиц d ср критическая скорость будет увеличиваться или же наоборот уменьшаться. Это подтверждает вышеприведённое утверждение о том, что в различных методиках расчётов имеются расхождения в значениях критических скоростей.
|
|
|
Можно предполагать, что приведённые формулы справедливы для определенного, возможно какого-то узкого диапазона значений d ср, D, P 1, но не для широкого интервала основных параметров гидротранспорта.
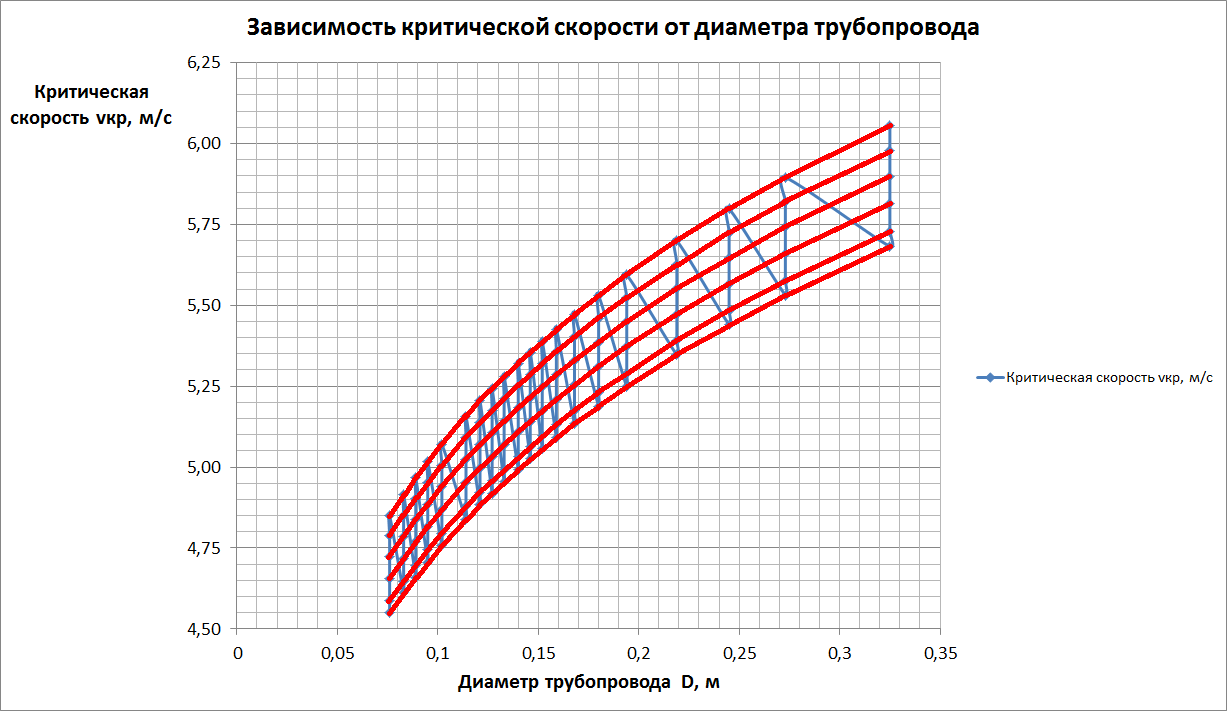
Рисунок 15 – График зависимости критической скорости от диаметра трубопровода D для d ср >1,5 мм
Но в тоже время, благодаря построенным графикам можно рассчитать необходимый диаметр трубопровода, зная средневзвешенный размер твёрдых частиц d ср.
Рассчитывать диаметр трубопроводов требуется так, чтобы скорость воды в трубе была выше критической скорости в 1,05–1,1 раз для тонкодиспресных гидросмесей, в 1,1–1,15 для грубодисперсных гидросмесей и в 1,15–1,2 раза для полидисперсных гидросмесей. Уменьшение скоростей приводит к резкому увеличению сопротивлений, потерь, а также появляется риск закупоривания насоса. Это объясняется тем, что распределение концентрации частиц по высоте весьма неравномерно.
В то же время, при скоростях движения гидросмеси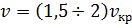 
большая часть твёрдых частиц движется в нижней трети сечения трубы. Вследствие этого происходит более интенсивный гидроабразивный износ нижней трети сечения трубы.
Гидроабразивный износ является результатом процесса постепенного изменения размеров, формы или состояния поверхности, происходящей в результате воздействия твёрдых абразивных частиц, взвешенных в жидкости и перемещающихся вместе с ней относительно изнашиваемой поверхности.
А.О. Спиваковским приведено минимальное значение критической скорости =1,6 м/с. [10] Б.Ф. Лямаев приводит максимальные значения скоростей для труб диаметром 0,2–1,0 в пределах 2,5–6 м/с. [11]
Для уменьшения удельных затрат энергоресурсов транспортирование шахтного шлама необходимо стремиться производить при скоростях близких к и высоких концентрациях твёрдого вещества в гидросмеси.
В настоящее время, для расчёта внутреннего диаметра нагнетательного шламопровода для размера частиц от 1 до 70 мм согласно «Пособию по проектированию гидравлического транспорта (к СНиП 2.05.07-85)» не приведено чётких и определяющих формул. Однако, в научно-технической литературе встречается следующая формула [12]:
(2.9)
где Q – производительность поршневого насоса, м3/ч; v кр - критическая скорость движения пульпы.
Одним из множителей делителя подкоренного выражения в данной формуле является критическая скорость . Данная формула не учитывает размер самих частиц. В данной работе было установлено, что значение критическая скорость в определённых диапазонах средневзвешенного размера твёрдых частиц d ср как зависят, так и не зависят непосредственно от значения d ср. Исходя из этого, можно предположить, что приведённая формула для расчёта внутреннего диаметра нагнетательного шламопровода не является корректной и учитывающей факторы и показатели, необходимых для проведения гидравлических расчётов гидротранспорта.
Полученные данные указывают нам на необходимость проведения дальнейших экспериментальных исследований в области гидравлического транспортирования шахтного шлама для выяснения и уточнения закономерности влияния размера частиц, диаметра трубопровода, консистенции шлама и удельного веса твёрдой составляющей на величину критических скоростей.
В данной работе не рассмотрена зависимость между подачей поршневого насоса и критической скорость . Необходимость исследования данной зависимости обусловлена определением оптимальных энергоэффективных режимов работы поршневого насоса и достижением минимального износа рабочих элементов насоса.
Выбор оптимальной критической скорости может предостеречь от выбора трубопровода большего диаметра, чем необходим для перекачки шахтного шлама с определённым средневзвешенным размером твёрдых частиц d ср и способствовать уменьшению гидроабразивного износа.
Вследствие осуществления и реализации результатов исследований ожидается увеличение экономической эффективности применения поршневых насосов для перекачки шахтного шлама и гидротранспортирования шахтного шлама.
Этап 3. Рассчитать общий напор, являющийся суммой статического напора, потерь в трубопроводной сети и дополнительного давления в трубопроводе.
Потери в трубопроводной сети состоят из потерь напора натрение потока и потерь, полученных в результате прохождения потока через фасонные части типа колен трубопровода, запорной арматуры и т.д.
Основой для расчёта потерь в трубопроводной сети в настоящее время служат полуэмперические и эмперические зависимости, полученные различными авторами [5].
В настоящее время требуемый расчетный напор насоса определяется по формуле:
(2.10)
где ΔНтр - потери напора по длине трубопровода, м; Нг – разность отметок оси насоса и отметки сливного отверстия трубопровода; ΔНм – местные потери напора (в арматуре), ΔНм=0,2 ΔНтр.
Потери напора при течении шахтного шлама по трубопроводу:
, (2.11)
где к – эмпирический коэффициент для породы к =1,4 [11]; ψ -коэффициент сопротивления при свободном падении в среде твердой частицы.
Для практических расчетов, ψ рассчитывается по формуле:
(2.12)
- коэффициент местных гидравлических сопротивлений при движении по трубопроводу, для отшлифованных грунтом труб.
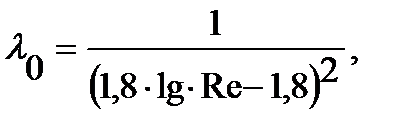(2.13)
Число Re:
, (2.14)
С -коэффициент, учитывающий весовое содержание R, % мелких классов, мельче 2 мм.
(2.15)
По статистическим данным горно-добывающих предприятий Южного Урала, число R принимается равным 95%;
(2.16)
νв =0,01007 см2/сек =1,007 10-6 м/с - кинематическая вязкость воды;
При малых значениях коэффициента С<0,3 значение Vкр следует увеличить на 15-20%, следовательно Vкр=1,16·1,15=1,334 м/с.
Фактическая скорость гидросмеси, м/с:
(2.17)
где Qп – производительность поршневого насоса, м3/ч.
Для предотвращения заиливания, необходимо учитывать и соблюдать условие Vгф ≥ Vкр.
Исходя из вышеизложенного условия, становится возможным учитывать минимальное значение производительности поршневого насоса Qп для последующего выбора непосредственно требуемого поршневого насоса.
Для откачивания шлама, следует подобрать трубопроводные отводы большего радиуса и запорную арматуру прямого прохода. Таким образом, можно пренебречь потерями на фасонных частях при расчётах общих потерь.
Теперь можно подобрать насос на основании значений расхода и напора.
Мощность привода для поршневого насоса (кВт) определяется по формуле [13]:
, (2.18)
где 
– коэффициент запаса, принимаемый 1,1-1,3 в зависимости от мощности привода; g – ускорение свободного падения; Q – подача (производительность) насоса, м³/с; H – расчетная высота подъёма, м; 
– плотность перекачиваемого шахтного шлама, кг/м³;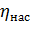 
– КПД поршневого насоса (0,9); 
- КПД передачи, равный 0,9-0,95;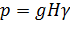 
- давление, развиваемое насосом, Па.
Также следует принять во внимание метод установки. Все эксплуатационные расходы, включая износ деталей, техническое обслуживание, энергопотребление, являются важными пунктами, которые следует учитывать для определения эффективности работы поршневого насоса.
Кривые мощности насосов основаны на данных для работы в чистой воде. Для определения мощности шламового насоса кривые мощности необходимо умножить на удельную массу шлама, для получения соответствующего значения мощности. Как правило, при эксплуатации насоса могут возникать ситуации, когда значения показателей шлама окажутся больше расчётных. Это может повлечь за собой выход насоса из строя. Для предотвращения данной ситуации необходимо выбирать привод насоса с запасом мощности. В настоящее время, производители рекомендуются выбирать 20% запас мощности.
|
|
|
