Обработка данных опроса с помощью метода наименьших квадратов

ДОМАШНЕЕ ЗАДАНИЕ

 

По дисциплине

«Организационно-экономическое моделирование»

 

Тема: «Функция спроса и метод наименьших квадратов»

 

Вариант №

 

(18)

 

 

Студент _______________________ ________Чуйко И.А.________

(Подпись) (ФИО студента)

 

Группа _____ИБМ2-72_______

(номер группы)

 

Преподаватель ________________ _________ Куликова С.Ю.__________

(Подпись) (ФИО преподавателя)

 

Москва

 

Цель домашнего задания:

На основе данных, полученных в процессе опроса потребителей, о максимально возможной цене, которую потребитель готов заплатить за пылесос, научиться строить выборочную функцию спроса и оценивать ее, искать цены, максимизирующие прибыль, и обрабатывать данные опроса с помощью метода наименьших квадратов.

 

Задачи домашнего задания:

1. Собрать информацию о максимально возможной цене (в руб.), которую потребители готовы заплатить за пылесос, опросив 50 человек;

2. На основе данных опроса построить выборочную функцию спроса;

3. Найти розничные цены, максимизирующие прибыль, для пяти различных значений оптовой цены;

4. Методом наименьших квадратов восстановить теоретическую функцию спроса, используя линейную аппроксимацию;

5. Рассчитать доверительные границы;

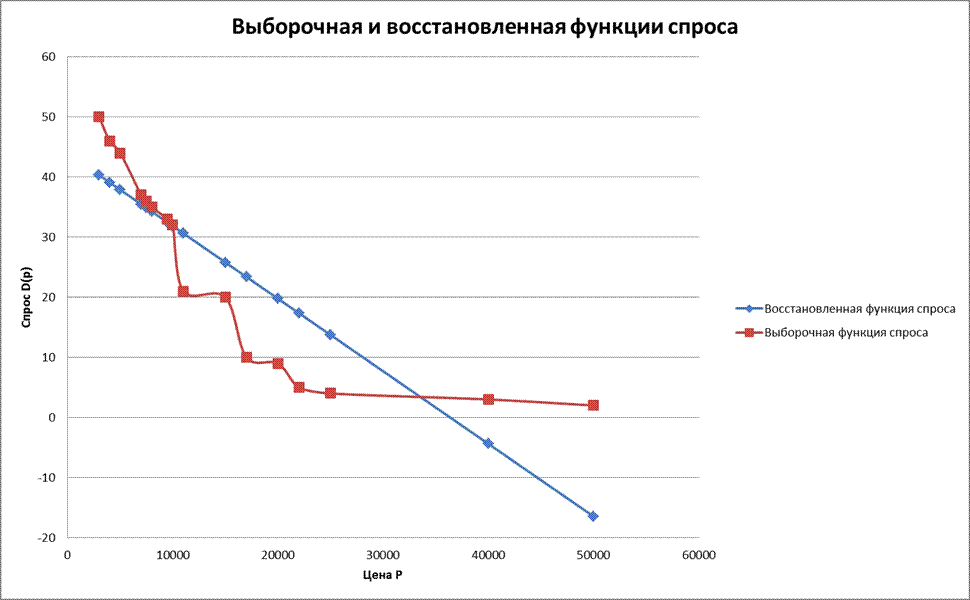
6. Построить на одном графике восстановленную и выборочную функции спроса;

7. На основе восстановленных зависимостей найти розничные цены, максимизирующие прибыль, для пяти различных значений оптовой цены, и сопоставить с результатами оптимизации на основе выборочной функции спроса;

8. Проделать аналогичные расчеты, используя степенную аппроксимацию.

 

 

Функция спроса

При маркетинговых исследованиях полезно проводить опрос потребителей, например, при вводе товара на рынок. Полезно знать, сколько денег потребители готовы заплатить за тот или иной товар, чтобы установить оптимальную цену. Затем необходимо обработать эти данные. Обработка данных проводится с помощью оценивания функции спроса. Это можно сделать, построив выборочную функцию спроса графически, в виде таблицы или обработав данные с помощью метода наименьших квадратов.

Рассмотрим первый метод (табличный).

В результате опроса 50 человек мы получили 50 ответов в ответ на вопрос, какую максимальную цену потребитель готов заплатить за пылесос. Цена колеблется от 3000 руб. до 50000 руб. Сначала соберем все цены:

8000, 15000, 5000, 50000, 15000, 15000, 5000, 5000, 3000, 3000, 10000, 10000, 10000, 10000, 5000, 25000, 20000, 20000, 5000, 5000, 5000, 10000, 3000, 15000, 50000, 8000, 15000, 15000, 10000, 20000, 10000, 7500, 10000, 10000, 3000, 40000, 20000, 7000, 15000, 4000, 4000, 10000, 15000, 15000, 11000, 10000, 9500, 22000, 17000, 15000

 

Теперь перейдем к анализу данных опроса. Для начала необходимо составить таблицу исходных данных – пар чисел (p, D (p)), где

p – независимая переменная (цена);

D (p) – зависимая от p величина (спрос).

Упорядочиваем все значения в порядке возрастания. Затем строим табл.1. В первом столбце – номера различных значений цены в порядке возрастания (i). Во втором столбце приведены сами значения цены (p_i).В третьем столбце указано, сколько раз названо то или иное значение (f_i). В четвертом столбце указан спрос D (p_i) на товар при его цене (p_i).

 

 

Таблица 1.

Оценивание функции спроса.

i	Цена (pi)	Ni	Спрос D (pi)

 

Таким образом, 50 опрошенных потребителей назвали 16 конкретных значений цены (максимально для них допустимых значений). Каждое из значений, как видно из третьего столбца табл.1, названо от 1-го до 7 раз.

Теперь легко построить выборочную функцию спроса в зависимости от цены. Она представлена в четвертом столбце, который заполняется снизу вверх на основе следующих рассуждений.

Если мы будем предлагать товар по ценам свыше 300000 руб., то его не купит никто. При цене 300000 руб. появляется 1 покупатель. Если цену понизить до 150000 руб., тогда товар купят двое – тот один, для кого максимальная цена 150000 руб., и тот один, кто был согласен на большую цену 300000 руб. Таким образом, четвертый столбец заполняется по правилу: значение в клетке 4-го столбца равно сумме значений в находящейся слева клетке 3-го столбца и в лежащей снизу клетке 4-го столбца.

З ависимость спроса от цены - это зависимость 4-го столбца D (p_i) от 2-го p_i. Зависимость можно представить на графике, в координатах "спрос- цена". Ордината - это спрос D (p_i), а абсцисса - цена p_i (рис.1).

Зависимость спроса от цены представим на графике: «спрос-цена», где абсцисса – спрос D(p_i), а ордината – цена p_i:

 

Рис 1. Функция спроса

Посчитаем прибыль при различных значениях издержек p ₀. Издержки – это либо оптовая цена, если товар закупается, либо - себестоимость единицы продукции, если товар производим сами. В нашем случае p ₀ – оптовая цена.

Найдем для каждого значения оптовой цены p ₀ оптимальную розничную цену (см. табл.2 на следующей странице). Предполагаемые оптовые цены:2500,4000,8000,15000,25000 (руб.). Для каждого i в табл.2 приведены произведения (p_i - p _0.) D (p_i), где p ₀ - это оптовая цена.

 

 

 

 

Таблица 2.

Расчет оптимальной цены.

 

i	Цена Pi	Ni	Спрос D (pi)	Прибыль (pi -2500) D (pi)	Прибыль (pi - 4000) D (pi)	Прибыль (pi - 8000) D (pi)	Прибыль (pi - 15000) D (pi)	Прибыль (pi - 25000) D (pi)
					-50000	-250000	-600000	-1100000
						-135000	-450000	-900000
							-287000	-697000
							-170000	-510000
								-280000
								-125000

Из этого графика видно, что чем выше становится цена, тем сильнее уменьшается количество желающих приобрести продукцию.

Найдем для каждого значения издержек p0 оптимальную цену:
• В случае издержек 2500 руб. оптимальной ценой будет 80000 руб.
• В случае издержек 4000 руб. оптимальной ценой будет 80000 руб.
• В случае издержек 8000 руб. оптимальной ценой будет 80000 руб.
• В случае издержек 15000 руб. оптимальной ценой будет 80000 руб.
• В случае издержек 25000 руб. оптимальной ценой будет 80000 или 90000 руб.

 

Обработка данных опроса с помощью метода наименьших квадратов

Рассмотренная ранее функция спроса построена на использовании тех значений цены, которые были названы при опросе. Пока мы не знаем, какой будет спрос при других значениях цены. Может быть, и оптимальная цена будет находиться вне названных при опросе значений.

Поэтому целесообразно восстановить функцию спроса при всех возможных значениях цены, а затем использовать эту восстановленную зависимость для расчета оптимальной цены при различных значениях издержек.

Восстановить зависимость можно с помощью метода наименьших квадратов.

 

Метод наименьших квадратов относится к важному разделу организационно-экономического моделирования и прикладной статистики - многомерному статистическому анализу. В многомерном статистическом анализе исходные данные - это как минимум пара чисел (t_i, X_i) (а не одно число).

Предполагается, что переменная X линейно зависит от переменной t, т.е.

X (t) = a (t – t _ср.) + b

Это - теоретическая модель, а практически известны исходные данные – набор пар чисел (t_i, X_i), i = 1, 2, 3, …, n, где:

t_i – независимая переменная (например, время, а в случае определения выборочной функции спроса - цена p_i),

X_i – зависимая переменная (например, индекс инфляции, курс доллара, а в случае определения выборочной функции спроса это будет спрос D (p_i)).

Предполагается, что переменные связаны линейной зависимостью:

X_i = a (t_i – t _ср.) + b + e_i , i = 1, 2, 3, …, n.

Это - реальная зависимость, учитывающая погрешности (e_i), искажающие зависимость, параметры a и b нам неизвестны и подлежат оцениванию, а

t _ср. = .

Обычно параметры a и b оценивают методом наименьших квадратов.

Согласно этому методу для расчета наилучшей функции, приближающей линейным образом зависимость X от t, следует рассмотреть функцию двух переменных:

f (a,b) = - a (t_i – t _ср) – b ]².

Фактически – это есть сумма квадратов разностей между реальными значениями функции и теоретически определенными значениями функции от независимой переменной.

Оценки метода наименьших квадратов – это такие значения a и b, при которых функция f (a,b) достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции f (a,b) по аргументам a и b, т.е. и , и приравнять их к 0.

Из полученных уравнений путем внутриматематических преобразований получим оценки:

,

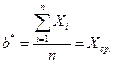
Следовательно, восстановленная функция, с помощью которой можно прогнозировать, имеет вид:

.

Это - теоретическая функция, в которой вместо параметров подставлены их оценки, что позволяет проводить прогнозирование на какой-то интервал независимой переменной t вперед, а также интерполировать эти данные на моменты между наблюдениями.

Если взять другие обозначения, то линейная зависимость может выглядеть так:

i = 1, 2, 3, …., n. (1)

Сравнивая выражения:

X_i = a (t_i – t _ср.) + b +e_i = at_i – at _ср. + b +e_i

и (1), легко перейти от одного к другому:

c =a, d = b – at _ср.

Аналогичные соотношения справедливы и для оценок:

c^* = a^*, d^* = b^* -a^*t _ср,

X_i^* = c^*t_i + d^*.

Оценкой погрешности (невязки) e_i является кажущаяся невязка

X_i - X_i^*.

Возникает вопрос, насколько точно оценивается зависимость. Чтобы ответить на него, надо ввести модель порождения данных:

,

где e _1, e ₂…… e_n - независимые, одинаково распределенные случайные величины с математическим ожиданием 0 и дисперсией .

Таким образом, модель описывается тремя параметрами: c, d и . Параметры c и d мы умеем оценивать, а для оценки ² используется следующая формула:

= ,

где SS - так называемая остаточная сумма квадратов, - оценка дисперсии.

Доверительные интервалы для прогностической функции записываются следующим образом (см. п.3.1 главы 3 настоящего учебника):

,

где ,

U () –квантиль стандартного нормального распределения порядка .

При доверительной вероятности = 0,95 находим из таблиц U () = 1,96, при = 0,99 имеем U () = 2,58, и U () = 1,64 при = 0,9.

Теперь перейдем к обработке данных опроса с помощью метода наименьших квадратов. Для начала необходимо составить таблицу исходных данных – пар чисел (p, D(p)) также в порядке возрастания значений параметра p (см. табл. 3 на следующей странице). Далее рассчитаем прогностическую функцию и оптимальную цену при различных уровнях оптовой цены.

 

 

i	Цена pi	Ni	piNi	Спрос D(pi)	D(pi)Ni	(pi^2)Ni	D(pi)PiNi	D*(pi)	Ni[D(pi)-D*(pi)]
								27,65
								27.59
								27,49
								27,43
								27,27
								27.11
								26,95
								26,79
								26,66
								26,41
								26,15
								25,19
								24,87
								24.55
								22,95
								18.15
Сумма
Сумма/n					27,14

 

 

Таблица 3.

ценивание функции спроса методом наименьших квадратов.

участников опроса.

	Ni[D(pi)-D*(pi)]^2	pi^2
Сумма	2137,48
Сумма/n	SS

 

 

Теоретическая функция спроса:

D ^*(p_i) = a (p - p _ср.) + b;

Перейдем к расчету восстановленной функции спроса:

D ^*(p_i) = a *(p - p _ср.) + b *.

Необходимо найти оценки параметров a* и b*:

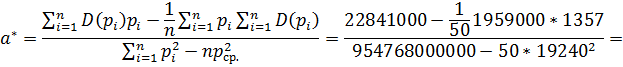
-0.000032

b * = 27,14; d * = b * - a * p _ср.= 27,14– (- 0,000032)*19240 = 27.75

Таким образом, восстановленная функция спроса имеет вид:

D *(p) = (-0,000032) p + 27.75

 

Из табл.2 видно, что остаточная сумма квадратов SS = 2137,48. Исходя из этого, найдем оценку среднего квадратического отклонения:

 

= = 6,53.

 

Затем найдем доверительные границы для функции спроса:

 

D ^*(p)_{верхн.\нижн.} = a^* p + d^* 1,96

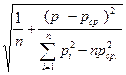
D ^*(p)_{верхн.\нижн.} = (-0,009) p + 62,1 1,96 =

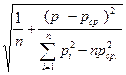= (-0,009)p_i +62,1 .

 

 

Из табл.3 видно, что остаточная сумма квадратов SS = 2795,81. Исходя из этого, найдем оценку среднего квадратического отклонения:

 

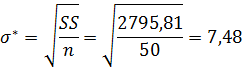
Затем найдем доверительные границы для функции спроса:

 

 

 

 

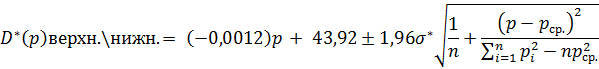
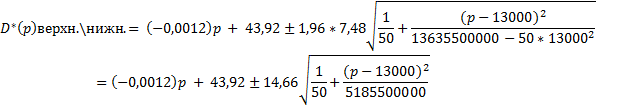
Например, при p = 8000

D ^*(8000) _верхн. = 34,32 + 2,31 = 36,63,

D^*(8000)_нижн. = 34,32 – 2,31 = 32,01.

Таким образом, при цене 8000 руб. товар купят 33-37 человек.

Рис.2. Выборочная и восстановленная функции спроса

Теперь перейдем к расчету оптимальной цены при различных уровнях издержек p ₀. Для этого мы должны максимизировать прибыль:

(p - p _0.) D ^*(p) = (p _. – p _0.)(a * p + d *).

Продифференцируем это выражение по p и приравняем 0 производную:

,

2 a * p _опт. – а * р ₀ + d * = 0,

p _опт. = .

Поскольку a * = -0,0012, a d * = 43,92,то

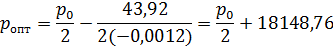
Как видно из последней формулы, при возрастании издержек оптимальная розничная цена также возрастает, но вдвое медленнее.

 

Сравним (табл.4) оптимальные цены, найденные с помощью метода наименьших квадратов (p _опт.2) и рассчитанные ранее с помощью первого метода (p _опт.1).

 

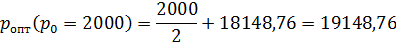
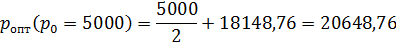
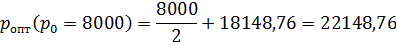
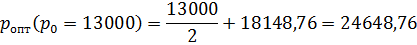
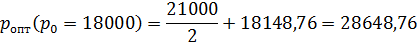
Таблица 4.

Сравнение методов расчета оптимальной цены.

p 0	p опт.2	p опт.1
	19148,76
	20648,76
	22148,76
	24648,76
	28648,76

 

 

Проанализируем результаты, представленные в табл. 3 и 4.

Согласно табл.3, при расчете восстановленной функции D *(p) при p = 40000 получаем отрицательную величину (-4,38), что не имеет смысла, т.к. спрос не может быть отрицательным. Рассмотри ситуацию подробнее. Функция спроса убывает, коэффициент a * отрицателен, поэтому рано или поздно прямая уйдет в отрицательную область. Это значит, что приближение функции спроса линейной зависимостью может быть корректно лишь на некотором отрезке, а не на всей прямой. Выясним, при какой цене спрос достигает 0:

D *(p) = (-0,0012) p +43,92 = 0,

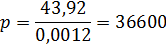
Т.е. корректное приближение функции спроса линейной зависимостью может быть при цене p меньшей, чем 36600 рублей.

Общепринятых простых методов, позволяющих избежать отрицательных оценок функции спроса, нет. Если получаем отрицательные величины, то должны указать область, в которой линейная зависимость дает корректную оценку, что и сделали выше, когда D *(p) приравняли к 0.

Рассмотрим теперь табл.4. Здесь видим разницу между расчетной оптимальной ценой p _опт.2, полученной с помощью метода наименьших квадратов, и расчетной ценой p _опт.1, найденной исходя только из данных опроса. Это связано с тем, что потребитель всегда склонен к круглым числам (например, большинство назовет 19000 руб., а не 19148 руб. 76 коп.). Мы же при применении метода наименьших квадратов ищем максимум не только среди названных опрощенными значений, а по более обширному множеству.

 

 

Нелинейные зависимости

Как проводить анализ данных, если функция спроса не является линейной? Есть два подхода – параметрический и непараметрический.

В первом случае подбираем подходящее семейство функций и по результатам измерения (опроса) оцениваем параметры. Степенное семейство:

D^** (p) = cp^{α .}

При этом полезно преобразование переменных, приводящее задачу к линейному виду. В случае степенного семейства необходимо прологарифмировать обе части последнего равенства. Тогда получим:

ln D^** (p) = ln c + ln p.

Затем обозначим:

у = ln D^** (p), x = ln p, d =ln c.

Исходя из введенных обозначений, имеем линейное уравнение:

у = x + d.

Задача оценивания параметров степенной зависимости сведена к ранее рассмотренной задаче оценивания параметров линейной функции.

Теперь перейдем к обработке данных опроса с помощью метода наименьших квадратов. Для начала необходимо составить таблицу исходных данных – пар чисел (x = ln p, у = ln D (p)) также в порядке возрастания значений параметра x (см. табл. 5 на следующей странице). Далее рассчитаем прогностическую степенную функцию.

 

Таблица 5.

Оценивание функции спроса методом наименьших квадратов.

 

i	Цена Pi	Спрос D(pi)	xi =ln(pi)	yi =ln D(pi)	fi	xi fi	yi fi	yi2fi	xi yi fi
			8,006368	3,912023		32,02547	15,64809202	256,4076865	125,2843765
			8,29405	3,828641		16,5881	7,657282793	137,5825189	63,50988359
			8,517193	3,78419		59,62035	26,48932744	507,798059	225,6147193
			8,853665	3,610918		8,853665	3,610917913	78,38739151	31,96985909
			8,922658	3,583519		8,922658	3,583518938	79,61383113	31,974515
			8,987197	3,555348		17,97439	7,110696123	161,5394134	63,90522559
			9,159047	3,496508		9,159047	3,496507561	83,88814337	32,02467736
			9,21034	3,465736		101,3137	38,12309493	933,1340674	351,1266803
			9,305651	3,044522		9,305651	3,044522438	86,59513219	28,3312619
			9,615805	2,995732		96,15805	29,95732274	924,6371503	288,0637881
			9,740969	2,302585		9,740969	2,302585093	94,88646972	22,42940914
			9,903488	2,197225		39,61395	8,788898309	392,3162628	87,04074501
			9,998798	1,609438		9,998798	1,609437912	99,97595609	16,09244415
			10,12663	1,386294		10,12663	1,386294361	102,5486575	14,0384916
			10,59663	1,098612		10,59663	1,098612289	112,2886677	11,64159314
			10,81978	0,693147		21,63956	1,386294361	234,1352042	14,99939762
∑						461,6377	155,2934052	4285,734612	1408,047067
∑/n						9,232753	3,105868104

 

Найдем оценки параметров α и b:

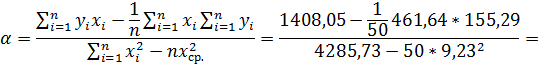
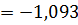
b = 3,106; d * = b - ax _ср.= 3,106 – (- 1,093)*9,23 = 13,198.

 

Получили выражение:

у = - 1,093 x + 13,198

α = - 1,093;

ln c = 13,198 – значит, c = e^13,198 = 539094,27.

Степенная функция имеет вид:

 

D^** (p) = 539094,27 p ^{- 1,093}

 

Графики степенной и выборочной функций спроса можно увидеть на рис.3. на следующей странице.

 

Рис.3. Выборочная и степенная функции спроса

Определим оптимальную розничную цену p _{опт .3} при различных значениях оптовой цены:

(p-p₀) D**(p) → max

Для случая степенной зависимости:

(p-p₀) cp^α → max

Точка, в которой достигается максимум, не меняется при умножении максимизирующей функции на константу. Поэтому задача принимает следующий вид:

(p-p₀) p^α = h(p) → max

Для нахождения максимума функции продифференцируем ее и приравняем производную к нулю:

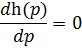
h’(p) = αp^α-1 (p-p₀)+ p^α = p^α-1 [ α (p-p₀)+ p ]

(1+ α) p = αp₀

Получаем формулу для расчета оптимального значения розничной цены, максимизирующего прибыль:

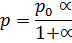
Сравним (табл.6) оптимальные цены, найденные с помощью метода степенной аппроксимации (p _опт.3) и рассчитанные ранее с помощью первого метода (p _опт.1).

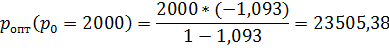
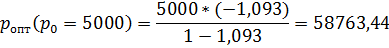
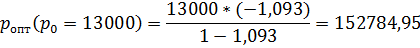
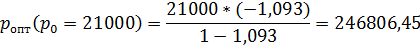
Таблица 6.

Сравнение методов расчета оптимальной цены.

p 0	p опт.3	p опт.1
	23505,38
	58763,44
	94021,51
	152784,95
	246806,45

Как можно заметить из табл.6, значения оптимальных цен p _опт.3, найденные с помощью метода степенной аппроксимации, сильно отличаются от значений p _опт.1 и при увеличении значения оптовой цены p ₀ резко возрастают. Это связано с тем, что функция, полученная при методе степенной аппроксимации, имеет вид гиперболы и, посмотрев на рис.3, можно заметить, что при увеличении цены график степенной функции не уходит в зону отрицательного спроса (как в случае с восстановленной линейной зависимостью), а бесконечно стремиться к асимптоте – оси абсцисс. Поэтому, если бесконечно увеличивать значение оптовой цены и рассчитывать для него оптимальную розничную цену, то полученные значения оптимальных цен тоже будут бесконечно возрастать и не входить в интервал цен от 3000 до 50000, полученный в результате опроса. Можно сделать вывод о том, что расчет оптимальных цен в методе линейной аппроксимации более точен, чем расчет оптимальных цен в методе степенной аппроксимации.

Поделиться:

Воспользуйтесь поиском по сайту: