 |
Вращение твердого тела (корабельного на волнении или сухопутного носителя)вокруг неподвижной точки
|
|
|
|
Пример выполнения расчетной работы № К3
(РЕГУЛЯРНАЯ ПРЕЦЕССИЯ)
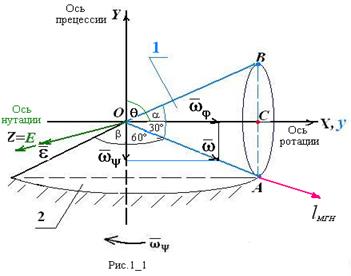
Дано. Конус 1 с углом 2a = 60° при вершине (рис. 1_1) катится по неподвижному конусу 2 с углом 2b=120° при вершине без скольжения, обегая последний 120 раз в минуту, приэтом вершина О конуса 1 остается неподвижной, а центр С его основания движется по окружности, расположенной в горизонтальной плоскости. Высота конуса 1 ОС= 10 см.
Определить. 1. Угол нутации q, угловые скорости нутации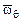 
, прецессии 
, ротации 
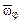и мгновенную угловую скорость 
.
2. Угловое ускорение конуса 
. 3. Скорости точек А, В, СÞ 
, 
, 
.
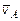4. Ускорения точек А, В, С Þ 
(найти осестремительное Þ 
и вращательное Þ 
ускорения точки С).
Решение. Введем неподвижную систему координат OXYZ с началом в точке О конуса 1. Поскольку конус 1 катится по неподвижному конусу 2 без скольжения, то скорости всех его точек, лежащих на образующей ОА, равны в данный момент времени нулю. Следовательно, мгновенная ось 
вращения конуса 1 совпадает с образующей ОА.
1. Угол нутации 
, поскольку с конца оси нутации ОЕ поворот от оси прецессии OY к оси ротации Oy кажется по часовой стрелке; 
.
2. Величина угловой скорости прецессии 
.
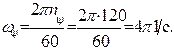
Направление вектора определим в зависимости от задания движения конуса 1, в данном случае вращение конуса 1 вокруг оси прецессии происходит по часовой стрелке, поэтому ¯ 
(оси прецессии).
3. Векторное равенство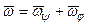 
, в котором линии действия всех его составляющих известны, позволяет определить как направление векторов всех составляющих угловых скоростей, так и их величины а именно: линией действия вектора является мгновенная ось вращения ; линией действия вектора ¯ - ось прецессии OY, линией действия вектора 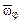- ось ротации Оy (рис. 1_1). Таким образом, величина мгновенной угловой скорости 
, а величина угловой скорости ротации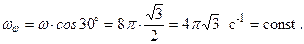 
.
|
|
|
4. Угловое ускорение в случае регулярной прецессии определяется векторным произведением 
, т.е. вектор 
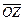, так какс конца оси OZ=ОЕ поворот от вектора к вектору кажется против хода часовой стрелки.
Величина углового ускорения 
рад/с2
5. Скорости точек конуса 1
* точки АÞ 
, так как в данный момент времени эта точка принадлежит мгновенной оси вращения конуса 1;
* точки В Þ 
, где 
, 
и вектор В 
.
* точки С Þ Т раекторией точки С,,с одной стороны, является окружность, плоскость которой перпендикулярна мгновенной оси вращения и центр которой лежит на , с другой стороны, – окружность, плоскость которой перпендикулярна оси прецессии ОY и центр которой лежит на этой оси. Поэтому
, (1)
где 
– кратчайшее расстояние от точки С до мгновенной оси ; 
= 
. Вектор 
, так как направление вектора совпадает с направлением мгновенной оси = ОА ивектор направлен таким образом, чтобы с конца этой оси = вращение конуса 1 казалось против хода часовой стрелки (рис.1_2.
С другой стороны, поскольку центр С основания конуса 1 движется по окружности, расположенной в горизонтальной плоскости, то
, (2)
где 
– кратчайшее расстояние от точки С до оси ОY,равное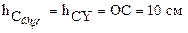 
. 
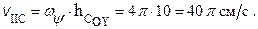
6. Ускорение какой-либо точки конуса 1 определим как геометрическую сумму осестремительного и вращательного ускорений.
ÞДля точки А: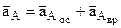 
; 
; так как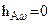 
где; 
см.
Вектор 
направлен перпендикулярно плоскости, в которой лежат векторы и 
, т.е. перпендикулярно ОА в сторону .
Таким образом, 
; 
.
ÞДля точки В: 
; 
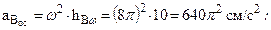
Вектор 
направлен от точки B к мгновенной оси вращения конуса 1 (рис.1_2).
, где 
см.
Вектор 
перпендикулярен плоскости, в которой лежат векторы и 
, принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОB в сторону . Величины этих векторов:;
Полное ускорение точки B найдем как диагональ прямоугольника, построенного на векторах 
:
|
|
|
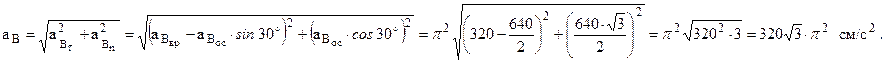
ÞДля точки С: а) 
; 
; 
.
Вектор 
направлен от точки С к мгновенной оси вращения кoнуса 1. Вектор 
перпендикулярен плоскости, в которой лежат векторы и 
, принадлежит плоскости ОXY, т.е. направлен перпендикулярно ОС в сторону (рис. 1_3);
б) 
; 
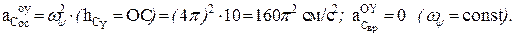
Ответ. 1). q =- p/2; ; 
1/с; 
1/с; 
1/с.
2) 
1/с2. 3). 
с м/с.
4) 
см/c2; 
см/с2; 
с м/с2.
|
|
|
