Динамическое программирование

Динамическое программирование(ДП)- это вычислительный метод, использующий аппарат рекуррентных соотношений. Разработан Р.Беллманом(США).

В ДП рассматриваются многоэтапные процессы принятия решений. При постановке и решении любой задачи в ДП формируется целевая функция и критерий, подлежащий оптимизации, и на каждом шаге принимается такое решение, чтобы досталась поставленная цель.

Метод ДП основан на принципе оптимальности:

Оптимальная стратегия обладает таким свойством, что каково бы ни было начальное состояние и начальные решения, последующие решения должны приниматься, исходя из оптимальной стратегии с учетом состояния, достигнутого путем предыдущих решений. Другими словами, планируя многошаговую операцию, необходимо выбирать решение на каждом шаге с учетом его будущих последствий на еще предстоящих шагах.

Основное преимущество метода ДП. Рассмотрим процесс с последовательным принятием решений, состоящий из n этапов, на каждом из которых принимается одно из k возможных решений. Тогда для определения оптимального решения методом полного перебора необходимо перебрать kⁿ что крайне велико (при n=10 и k=3 kⁿ≈ 59000). Метод ДП исключает необходимость полного перебора всех kⁿ возможных решений.

Рассмотрим применение ДП на примере задачи определения кратчайшего пути в графе.

 

7 Шаги процесса принятия решений определим

1 3 как последовательный выбор ребер графа,

6 5 приводящих в каждую вершину.

2 Выведем функциональное уравнение

Метода ДП. Пусть кратчайшее расстояние от вершины j

8 4 3 до конечной n=6 равно W_j, j=n-1,n-2,…,1. Рассмотрим

6 7 2 любую вершину k, k=1,2,…,n-1. Кратчайшее расстояние от

4 от k-й вершины до последней (n-й) будет равно

6 2 W_k=min_j(W_j+w_kj), где w_kj- длина ребра k→j.

(минимум берется по всем вершинам j, в которые можно

0 попасть из k-й).

 

Это и есть функциональное уравнение (k=n,n-1,…,1)

 

 

W₆=0 → для удобства сразу обозначаем на графе около соответствующей вершины.

W₅=0+2=2

 

W₄= min 4+2 =6 Кратчайший путь имеет длину 7 и соответствует дугам 1→2→5→6.

 

W₃=min 3+7 =5

7+6

2 5

4+2

W₂=min 8+6 =6

2+5

1 2

W₁=min 1+6 =7

3+5

 

Остовные деревья графа

Остовным деревом для связного неориентированного графа G=(V,E) с n вершинами называется неориентированное дерево, содержащее все n вершин и (n - 1) ребер графа. Таким образом, остовное дерево связывает все вершины графа и из каждой вер­шины графа можно попасть в любую другую. В полном графе с n вершинами имеется n ^n-2 остовных деревьев. Для одного и того же графа можно построить несколько остовных деревьев.

 

 

а б в   Рис. Граф (а) и его остовные деревья (б) и (в)

 

Пусть G=(V,E) — связный неориентированный граф и T = (V,F) — остовное дерево для него. Тогда:

а) для любых двух вершин vi и vj путь между ними единствен;

б) если к остовному дереву Т добавить ребро из (E-F), т.е. из оставшихся, не включенных в дерево ребер графа, то возникнет ровно один цикл и Т перестанет быть деревом.

Под остовным деревом ориентированного графа понимают такое дерево, в котором одна из вершин графа связана со всеми остальными.

Основными задачами нахождения остовных деревьев графа являются:

• нахождение остовного дерева;

• нахождение минимального и максимального остовного дерева.

 

Обходы графов.

Поиск в глубину и поиск в ширину

 

При решении многих задач, связанных с графами, необходим систематический обход вершин и ребер графа. Широкое применение получили два метода обхода:

• поиск в глубину;

• поиск в ширину.

При поиске в глубину осуществляется регулярный обход графа по следующим правилам.

1. Находясь в вершине v, нужно двигаться в любую другую w, ранее не пройденную вершину (если таковая найдется), одновре­менно запоминая дугу z, по которой мы впервые попали в вер­шину v.

2. Если из вершины v мы не можем попасть в ранее не прой­денную вершину или таковой вообще нет, то мы возвращаемся в вершину дуги z, из которой впервые попали в вершину v, и про­должим поиск в глубину из этой вершины.

При выполнении обхода по этим правилам мы стремимся про­никнуть вглубь графа как можно дальше, затем отступаем на шаг и снова стремимся пройти вперед и т.д.

При поиске в глубину в ориентированном графе мы можем попасть в вершину w из вершины v только в том случае, есливорграфе есть дуга (v,w), то есть двигаемся вперед только в направ­лении ориентации дуг, а возвращаемся против ориентации. В неориентированном графе таких ограничений нет. В неориентирован­ном графе обход можно начинать с любой вершины. Топология полученного остовного дерева зависит от начальной вершины.

Рассмотрим особенности поиска в глубину в орграфе. Те дуги, которые ведут к новым вершинам, называются дугами дерева, или древесными дугами. Они формируют для данного графа либо остовное дерево (дерево поиска в глубину), либо остовный лес (глу- бинное остовное дерево, глубинный остовный лес). Для того чтобы после завершения обхода в глубину все вершины оказались прой­денными и образовалось остовное дерево, (а не лес), необходимо и доста­точно, чтобы обход начинался во входе графа (вершине, имею­щей только исходящие дуги) и этот вход был единственным. В противном случае при обходе в глубину образуется глубинный остовный лес. Если при поиске в глубину вершины графа нумеру­ются в порядке их посещения, то такая нумерация называется глубинной нумерацией графа или М-нумерацией вершин графа [14].

После завершения поиска в глубину все дуги орграфа разби­ваются на 4 класса:

1) класс Т (Tree) древесных дуг, порождающих дерево поиска в глубину либо глубинный остовный лес. Для каждой дуги (x,y) Т имеем М(х) < М(у), М[i] — номер вершины i;

2) класс F (Forward) прямых дуг, к которому относятся дуги (x,y) такие, что М(х) < М(у) и вершина х соединена с y альтернативным путём, состоящим из древесных дуг. Другими словами, прямые дуги идут от предков к непосредственным потомкам, но не являются дре­весными дугами, а дублируют путь из древесных дуг;

3) класс В (Back) обратных дуг, представляющих дуги (х,у), такие, что М(х) > М(у) и вершина у соединена с х путем, состоя­щим из древесных дуг. По-другому обратные дуги идут от по­томков к предкам;

4) класс С (Cross) поперечных дуг, представляющих собой дуги (х,у), такие, что М(х) > М(у) и вершины х и у не соединены путем, состоящим из древесных дуг, т.е. поперечные дуги соединяют вер­шины, не являющиеся ни потомками, ни предками друг друга.

Рассмотрим пример:

Древесные дуги: (а, Ь), (Ь, е), (е, h), (h, j), (е, d), (а, с), (с,f), (f, i), (i,g).

Прямые дуги: (b, d), (с, g).

Обратные дуги: (g, i), (d, b).

Поперечные дуги: (f, h), (i, h):

 

Если начать с “C”

a

b

c

e

g

i

j

h

f

d

j

h

a

b

e

d

c

f

g

i

Рис. Обход дерева в глубину

 

 

j

h

a

b

e

c

f

g

i

d

Глубинное остовное дерево

 

Если начать обход в глубину этого же графа, начиная с другой вершины, то образуется глубинный остовный лес. Например, обход, начиная с вершины с, приведет к образованию леса с двумя остовными деревьями. Первое дерево включает ребра (с, f), ( f, h), (h, j), (f, i), (i,g).

Второе дерево с началом обхода в вершине а состоит из ребер (a, b), (Ь, e), (e, d). Для упражнения определите прямые, обратные и поперечные дуги графа, полученные в результате такого обхода.

При поиске в глубину в связном неориентированном графе образуется одно единственное глубинное дерево. В нем различа­ют только два класса ребер: древесные и обратные.

Сложность алгоритма поиска в глубину равна 0(m), где m — число дуг (ребер) графа.

При поиске в ширину последовательно просматриваются, начиная с заданной вершины, все вершины дерева на уровне k=1, 2,….

На рисунке представлены граф и остовные деревья полученные поиском в глубину и ширину. Начало поиска идёт с вершины 3.

 

а б в Граф и его остовные деревья: а) исходный граф; б) поиск в глубину; в) поиск в ширину

Если начать поиск с вершины 1, то получим:

 

При поиске в глубину; При поиске в ширину

Остовное дерево наименьшей стоимости (минимального веса)

Пусть G = (V, Е) — связный взвешенный неориентирован­ный граф, для которого задана матрица смежности, отобража­ющая веса ребер в числа (вещественные или целые). Стоимость (вес) остовного дерева определяется как сумма стоимостей (весов) его рёбер. Цель — найти для графа G остовное дерево наимень­шей стоимости (минимального веса).

Применение остовных деревьев минимальной стоимости можно найти при разработке коммуникационных сетей. Здесь вершины графа представляют города, рёбра – возможные коммуникационные линии между городами, а стоимость рёбер соответствует стоимости коммуникационных линий. В этом случае остовное дерево минимальной стоимости представляет коммуникационную сеть, объединяющую все города коммуникационными линиями минимальной стоимости.

Полный граф с n верши­нами содержит n ^n-2 остовных деревьев. Поиск каждого остовно­го дерева занимает 0(m) времени. В полном дереве m=n*(n-1)/2 (количество рёбер).

Тогда решение задачи прямым поиском имело бы сложность 0(n^n-2 n(n - 1)/2)=0(nⁿ).

 

Построение остовного дерева минимальной стоимости.

1. Алгоритм Прима

 

Наиболее простым алгоритмом поиска остовного дерева ми­нимального веса является алгоритм Прима, похо­жий на алгоритм Дейкстры поиска кратчайшего пути.

Алгоритм Прима заключается в следующем.

1. Вначале выбираем некоторую вершину V и включаем её в множество 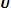выбранных величин, остальные (n-1) вершины графа отмечаются как невыбранные.

2. Определяются веса между всеми выбранными вершинами из 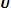и остальными невыбранными вершинами.

3. Выбираем вершину w с наименьшим весом до нее, фиксируем выбранные ребро и его вес.

4. Выбранную вершину w исключаем из множества невыбранных, включаем её в множество 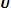, число невыбранных вершин уменьшаем на 1.

5. Пункты 2— 4 повторяем до тех пор, пока не будут выбра­ны все вершины, т.е. (n- 1) раз.

Процесс поиска остовного дерева наименьшего веса по алго­ритму Прима можно проследить на примере графа, приведенно­го на рисунке.

 

 

Номер итерации	w	Множество U выбранных вершин	Невыбранные вершины VU и веса дуг до них	Выбранная дуга и её вес
	–		2 3 4 5 6 7 8 9 7 10 - - - - - - -	1→2:7
		1,2	3 4 5 6 7 8 9 10 9 27 - - - - - -	2→4:9
		1,2,4	3 5 6 7 8 9 10 (1→3) 27 11 - - 8 (4→3)	4→3:8
		1,2,4,3	5 6 7 8 9 27 11 - - 31	4→6:11
		1,2,4,3,6	5 7 8 9 27 15 17 31	6→7:15
		1,2,4,3,6,7	5 8 9 27 17 31 15 (7→5 ) 21(7→8)	7→5:15
		1,2,4,3,6,7,5	8 9 (6→8) 17 31 (7→8)21	6→8:17
		1,2,4,3,6,7,5,8	31 (3→9) 32(8→9)	3→9:31
		1,2,4,3,6,7,5,8,9	–	–

 

Временная сложность алгоритма Прима равна O(). При большом значении n его использовании нерационально.

 

2. Алгоритм Крускала

 

Пусть имеется связный взвешенный граф G(V,E) с n вершинами. Построение остовного дерева минимального веса начинается с графа T(V,Ф), имеющего только данные n вершин без рёбер, т.е. состоящего из n связных компонент.

Построение дерева сводится к формированию набора связных компонент, постепенным объединением которых и формируется остовное дерево.

Алгоритм Крускала заключается в следующем.

1. Примем номер итерации i=1, упорядочим рёбра множества E по возрастанию их веса.

2. Выберем из множества E ребро с наименьшим весом.

3. Проверим выполнения условия: если ребро 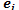связывает две вершины из разных компонент, то оно добавляется в граф T, в противном случае это ребро отбрасывается (т.к. его добавление в графу приведёт к образованию цикла).

4. Ребро исключается из множества E;

Осуществляется переход к новой итерации i=i+1, и шаги 2-4 повторяются до тех пор, пока все вершины не будут принадлежать одной компоненте.

Продемонстрируем работу алгоритма Крускала на примере графа, рассмотренного в предыдущем разделе.

 

 

Вес	Вершины	Признак выборки
			+
			+
			+
			-
			+
			+
			+
			+
			-
			-
			+
			Конец выборки

Упорядоченная таблица весов рёбер графа

 

 

Временная сложность алгоритма Крускала O(), где m – количество рёбер в графе. При m алгоритм Крускала предпочтительнее алгоритма Прима, но если m близко к , то рекомендуется применять алгоритм Прима.

 

Упорядочение ориентированного графа (топологическая сортировка)

Часто встречаются ситуации, когда необходимо решать задачу сортировки элементов множества, для которых определен частичный порядок, т.е. упорядочение задано не на всех, а только на некоторых парах элементов. Вот два примера:

1. В учебных программах вузов одни предметы опираются на материал других. Топологическая сортировка означает чтение курсов в таком порядке, чтобы ни один курс не читался раньше того курса, на материале которого он основан.

2. Сетевые методы планирования и управления предполагают, что любая работа может быть выполнена только после того, как будут выполнены опорные работы.

Пусть имеется ориентированный граф G=(V,E) с произвольно занумерованными вершинами v_i­, i_­­= 1,2,…,n. Граф является упорядоченным, если в отношении каждой его дуги (v_i­, v_j) справедливо неравенство v_i­<v_j. Для этого необходимо выполнить перенумерацию вершин в соответствии с их рангами. Будем считать, что единственная вершина v_i­, не имеющая входов, имеет нулевой ранг. Для любой другой вершины v_j ее ранг равен максимальной длине пути (максимальному числу дуг) от вершины нулевого ранга v_i­ до вершины v_j.

Рассмотрим граф, представленный на рисунке. Из рисунка видно, что вершина 3 имеет ранг R=0, вершина 1 имеет ранг R=1, вершины 5 и 7 имеют ранг R=2, вершина 4 имеет ранг R=3, вершина 2 имеет ранг R=4 и вершина 6 имеет ранг R=6.

 

 

 

а)Неупорядоченный граф б) Упорядоченный граф

Алгоритм упорядочения графа состоит из двух этапов. На первом этапе определяются ранги вершин, на втором этапе осуществляется перенумерация их в соответствии с рангами. Единственной вершине v_j, не имеющей входов, присваивается номер 0, а затем нумерация вершин одного ранга безразлична. Упорядоченный граф имеет вершины v_j с номерами 0,1,2,…,n – 1.

Рассмотренный выше граф после упорядочения будет иметь нумерация вершин, как показано на рисунке.

Таким образом, исходным номерами вершин 1,2,3,4,5,6,7 после упорядочения соответствуют новые номера 1,5,0,4,2,6,3.

 

Поделиться:

Воспользуйтесь поиском по сайту: