Матричные представления графов

ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Теория графов — это раздел математики, включающий в себя систему терминов и обозначений, которые позволяют сравнительно просто опи­сывать сложные процессы и явления. Началом возникновения теории графов явилась задача о кенигсбергских мостах, которую решил Л. Эйлер. Задача заключалась в том, чтобы пройти по семи мостам только один раз и вернуться в исходную часть города.

Само название «граф» предполагает графическую интерпретацию изучаемого явления.

Графом G = (X,U) называется совокупность двух множеств: непусто­го множества X (вершин) и множества U (ребер), т.е.

Обычно граф изображают диаграммой: вершины — точками или кружочками, а ребра — линиями.

Если ребра графа ориентированы, т.е. показаны стрелкой от вершины к вершине, то они называются дугами, а такой граф называется ориенти­рованным или орграфом (рис. 10.1). Если ребра не имеют ориентации, то граф называется неориентированным или неографом (рис. 10.2).

Каждая дуга соединяет две вершины графа, одна из которых являет­ся начальной, другая конечной и направлена от первой вершины ко вто­рой. Обозначают дуги: U₁ = (x_vx₂), U₁ или (x_v x₂).

Рис. 10.1. Орграф

Рис. 10.2. Неограф

Для орграфа на рис. 10.1 соответствие Т(х_]) = {х₂,х₃,х₄}, т.е. вершины х₂, х_г, х₄ являются конечными вершинами дуг, у которых начальной вер­шиной будет x_v

Примеры.

Г(х₂) = { х₁,х₃} (рис 10.1);

Г (х₅) = — пустое множество;

Г(х₃) = { х₄,х₃ }

В случае неографа, предполагается, что соответствие Г задает такой ориентированный граф, который получается из исходного графа заменой:

каждого ребра двумя противоположно направленными дугами, соеди­няющими те же вершины. Например, для неографа, приведенного на рис. 10.2, Г(х₃) = { х₁, х_2, х₃ } и т.д.

Так как Г(х_i) представляет множество вершин х_к ξ X, для которых в G существует дуга (х_к, х_i), то через Г^-1 (х_i) обозначают множество вершин х_к для которых в графе существует дуга (х_к, х_i), и называют обратным со­ответствием. Например, для орграфа G, рис. 10.3

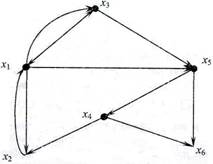
Рис. 10.3

Если отображение Г(х_i) распространяется не на одну вершину, а на мно­жество вершин Х_m = {x₁, х₂,..., х_m}, то под Г(х_m) понимают объединение

Г(х₁) U Г(х₂) U... U Г(х_m)

Например, для орграфа рис. 10.3 соответствиями будут

Г({х₂, х₃}) = {x₁ х₅}, Г({х₁, х₄}) = {х₂, х₃, х₅, х₆}.

Отображение Г(Г(х_i)) записывают Г²(х_i).

Тройное отображение Г(Г(Г(х_i))) записывают Г³(х_i) и т.д.

Для орграфа, рис. 10.3 запишем

С каждой вершиной графа связаны два множества (соответствия Г⁺(х_i) и Г^-(х_i)). Г⁺(х) — множество тех смежных с х_i - вершин, в которые заходят дуги из х_i. Г^-(х_i) — множество таких вершин смежных с х_i, из которых выходят дуги, заканчивающиеся в х_i.

Вершины x_i и х_к называются смежными, если существует дуга (ребро) U(х_i,х_к) соединяющая их. Например, (x₁,x₂), (x₁, х₃), (x₁, x₄), вершины х₂ и х₃ не являются смежными, рис. 10.1.

Если вершины х_i и х_к являются концами дуги U (х_i,х_к), то говорят, что эти вершины инцидентны дуге U (или дуга U инцидентна верши­нам х_i,х_к).

Степенью или валентностью вершины графа называется количест­во инцидентных ей дуг (ребер) и обозначается d(x_i) = Г(x_i). Например, d(x₁) = 4, d(x₂) = 2 (рис. 10.1).

Вершина, степень которой равна нулю, называется изолированной d(x₅) = 0 (рис. 10.1).

Число дуг орграфа, которые имеют вершину х_i своей начальной вер­шиной называется полустепенью исхода и обозначается d⁺(x_i).

Аналогично, количество дуг орграфа, которые имеют вершину х_к конечной вершиной, называется полустепенью захода и обозначается d^-(x_i).

Например, d⁺(x₁) = 3, d⁺(x₂) = 1, d^-(x₁) = 1, d^-(x₄) =.2.. (рис. 10.1).

Теорема Эйлера. Сумма степеней вершин графа равна удвоенному количеству дуг (ребер):

где n — число вершин графа, m — число дуг.

Следствие 1. Число вершин нечетной степени всегда четно.

Следствие 2. Сумма полустепеней вершин орграфа равна удвоенному числу дуг:

Путем (или ориентированным маршрутом) орграфа называется по­следовательность дуг, в которой конечная вершина любой дуги, отличной от последней, является начальной вершиной следующей. Например, пути из вершины х₁ в вершину х₄ орграфа рис. 10.1.

Ориентированной цепью (орцепью) или простым путем называет­ся такой путь, в котором каждая дуга используется не более одного раза.

Простой орцепью (элементарным путем) называется путь, в кото­ром каждая вершина графа применяется не более одного раза.

Маршрут — это неориентированный «двойник» пути, и это понятие рассматривается в тех случаях, когда можно пренебречь направленно­стью дуг в орграфе. Маршрутом называется последовательность ребер u₁, u₂,...,u_n, в которой каждое ребро u_i, за исключением, возможно, пер­вого и последнего ребер, связано с ребрами u_i-1 и u_i+1 своими двумя кон­цевыми вершинами.

Последовательность дуг

(10.1)

(10.2)

(10.3)

 

в орграфе, рис. 10.4, являются маршрутами. Черта над дугой указывает исключение ориентации дуг, т.е. дуги рассматриваются как ребра. Мар­шруты различают простые и цепи (ребро в таком маршруте использует­ся только один раз) и элементарные или простые цепи, в которых верши­на встречается только один раз. Например, маршрут М₁ (10.1) — простой маршрут (цепь) и элементарный маршрут М₂ (10.2) является простым маршрутом (цепью), М₃ (10.3) не является ни цепью, не простой цепью.

Петлей называется дуга графа, у которой начальная и конечные вер­шины совпадают и₆(х₃,х₂) (рис. 10.1).

Путь и_1, и₂,, и ₃,...., и_n называется замкнутым, если внем конечная вершина дуги и_п совпадает с начальной вершиной дуги u₁

Замкнутые пути в орграфах называются контурами.

Замкнутые маршруты (цепи) в неографах называются циклами.

Если дугам орграфа G ставится в соответствие какое-либо число, то говорят, что дуга имеет пропускную способность, величина которой — расстояние между вершинами или время прохождения точки, илиобъем

 

Рис. 10.4

перевозимого и т.д. Если дуга u = (x_i,x_k), приписывается число c_ik, назы­ваемое пропускной способностью дуги, а граф G называется графом со взвешанными дугами.

10.2. Разновидности графов

1. Подграфы или суграфы

Пусть дан граф G = (X,U) (рис. 10.5). Остовным подграфом G_p графа G называется граф, для которого X = X, т.е. остовный граф имеет

то же самое множество вершин, но множество дуг подграфа G_p является подмножеством множества дуг исходного графа (рис. 10.6).

Порожденным подграфом G_t, называется граф G_t = (Х_t, Г_t), для кото­рого 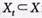и для каждой вершины т.е. порожден­ный подограф состоит из подмножества вершин Х_t множества вершин исходного графа и всех таких дуг графа G, у которых конечные и началь­ные вершины принадлежат подмножеству X_t (рис. 10.7).

Подграфом G_n = (Х_n, U_n) или частичным подграфом G = (X,U) явля­ется граф, для которого выполняется условие (рис. 10.8).

2.Граф G = (X,U) называется полным, если для любой пары вершин существует дуга (ребро). Примером такого графа является любой много­угольник с проведенными в нем всеми диагоналями, а каждая вершина имеет петлю (рис. 10.10).

3.Граф G = (X,U) называется симметричным (рис. 10.9), если в мно­жестве дуг U для любой дуги (x_i,x_k) существует также противоположно направленная дуга (х_к, х_i). В противоположном случае граф называется ассиметричным (рис. 10.8).

 

Рис. 10.5

 

Рис. 10.6

Рис. 10.7

Рис.10.8

 

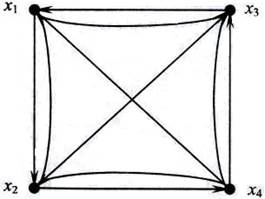
Рис. 10.9

 

Рис. 10.10

4. Двудольным графом (биграфом или четным) G = (Х,U) называ­ется такой граф, у которого множество X вершин разделено на два непе­ресекающихся множества Х₁ и Х₂, т.е.

причем всякое ребро (дуга) из U соединяет вершину из Х₁ с вершиной из Х₂. Мно­жества Х₁ и Х₂ называются долями такого графа (рис. 10.11).

Рис. 10.11

5. Мультиграфом называется граф, у которого две смежные вершины х_i и х_к соединены более чем одной дугой (ребром) в одном и том же на­правлении (рис. 10.12).

 

Рис. 10.12

Наибольшее число дуг (ребер) графа определяет его кратность.

6. Изоморфные графы

Термин «изоморфный» означает в переводе с латинского (иос — рав­ный, одинаковый и морфи — форма, вид), т.е. одинаковый по форме. Гра­фы на плоскости можно представить различными диаграммами. Два графа G₁ и G₂ называются изоморфными, если они имеют одно и то же число вершин и две любые вершины х_i и х_к одного графа соединены реб­ром (дугой), то и соответствующие им вершины другого графа тоже со­единены ребром (рис. 10.13). Обозначаются G₁ ~ G₂.

На рис. 10.13 указаны три изоморфных графа G₁, G₂, G₃.

 

Рис. 10.13

7. Древовидные графы являются простейшим классом графов и самым распространенным видом графов, применяемых в программи­ровании.

Древовидным графом (деревом) называется неориентированный связный граф с числом вершин не менее двух, не содержащий петель и циклов (рис. 10.14).

Рис. 10.14

Вершины, инцидентные только одному ребру дерева, называются ви­сячими (х₃ х₄, х₅, х₆ и х₇).

Ориентированным называется древовидный граф без циклов, в ко­тором полустепень захода каждой вершины, за исключением одной, например, вершины х_о, равна единице, а полустепень захода вершины х₀ равна нулю. Вершина х₀ называется корнем дерева (рис. 10.15).

Рис. 10.15

ОПЕРАЦИИ НАД ГРАФАМИ

1.Удаление вершин или ребер — это операция, с помощью которой можно из заданного графа G = (X,U) получить граф с меньшим числом элементов (вершин и ребер).

2.Добавление ребра — это операции по соединению несмежных вер­шин графа.

3.Объединение графов. Граф G₃ является наложением графов G₁ и G₂ (рис. 10.16).

 

Рис. 10.16

4. Произведение двух графов G_l и G₂ есть граф G, для которого x_1• x₂= G (рис. 10.17).

Рис. 10.17

5. Стягивание ребра означает отождествление смежных вершин (рис. 10.18).

Рис. 10.18

6. Расщепление вершин — это операция двойственная стягиванию ребра (рис. 10.19)

Рис. 10.19

МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ

Графы можно задавать с помощью матриц. Построим некоторые из них.

Матрицей смежности вершин графа называется квадратная матрица А = { a_ik } размером п х п,у которой строки и столбцы соответствуют вер­шинам, а элементы a_ik определяют из условий:

Для орграфа (рис. 10.20) построить матрицу смежности A(G).

Рис. 10.20

Матрицей инциденций B(G) = {b_ik] орграфа G = (X,U) называется прямоугольная матрица размерности п х т (п — число вершин графа, m — количество дуг), элементы которой удовлетворяют условиям:

В матрице инциденций для неографа при ее построении элементы -1 следует заменить на 1.

Построим матрицу B(G) инциденций для орграфа G (рис. 10.20).

 

Матрицей пропускных способностей дуг C(G) = {c_ik} графа G назы­вается квадратная матрица размерности n х n, элементы которой опреде­ляют из условий:

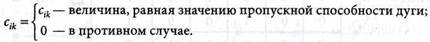
Матрицу пропускных способностей дуг С = (G) можно построить на основании матрицы смежности А = (G), в которой 1 заменяются значе­нием c_ik пропускной способности соответствующей дуги графа.

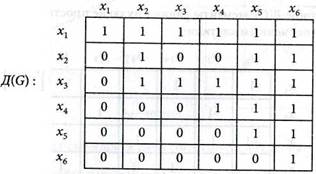
Матрицей достижимостей D(G) = {d_jk} графа G называется квадрат­ная матрица размерности п х п (п — число вершин орграфа), элементы которой удовлетворяют условиям:

Пример 10.1.

Для заданного графа G = (X,U) диаграммой записать в аналитической форме, составить матрицы: A(G) - смежности, B(G) — инциденций, C(G) — пропускных способностей дуг и D(G) — достижимостей.

Определить экстремальные пути и маршруты из х₁ в х₂.

Решение

1. Запишем граф G = (X,U) аналитически согласно определению

X = { x₁,x₂,x₃,x₄,x₅,x₆ }

где X — множество вершин; и — множество дуг орграфа (рис. 10.21).

 

Рис. 10.21

 

Строим матрицу смежности A(G) согласно определению:

Справа и снизу матрицы смежности А указаны полустепени исхода и захода вершин соответственно. Нули в матрице A^-(G) не указаны.

3. Строим матрицу инциденций B(G) на основании условий:

В матрице B(G) элементы равные нулю не проставлены и соответст­вуют незаполненным клеткам:

 

В матрице B(G) сумма элементов (1 и -1) равна нулю, что может быть проверкой построения матрицы.

 

4. Составляем матрицу пропускных способностей дуг C(G) = {c_jk} наосновании матрицы смежности A(G), заменяя элементы, равные 1 соот­ветствующими значениями пропускных способностей дуг, указанными на орграфе (рис.10.21). Нулевые значения пропускных способностей в матрице C(G) не записаны.

5. Строим матрицу достижимостей D(G) графа согласно определению:

6. Определяем значения путей из вершины x₁ в вершину x₆ способом перебора без учета петли U₉

7. Находим значения элементарных маршрутов из х_х в х₆, не учитывая ориентации дуг и исключая рассмотренные пути.

 

 

12	Поделиться:

Воспользуйтесь поиском по сайту: