Получение инверсной заселённости, состав активной среды, температурный режим, регенератор

Введение

       Из всех существующих лазеров (“Light Amplification by Stimulated Emission of Radiation”) длительного действия наиболее мощными, продвинутыми в практическом отношении и приспособленными для резки материалов, сварки металлов, термического упрочнения поверхностей деталей и ряда других операций являются электроразрядные СО₂-лазеры. Большой интерес к СО₂-лазерам объясняется также и тем, что у этого лазера эффективность преобразования электрической энергии в энергию лазерного излучения в сочетании с максимально достижимой мощностью или энергии импульса значительно превосходит аналогичные параметры других типов лазеров. С помощью их излучения производят необычные химические реакции, разделяют изотопы. Имеются проекты передачи энергии с помощью СО₂-лазеров с Земли в космос или из космоса на Землю, обсуждаются вопросы создания реактивного двигателя, использующего излучение лазера. За 33 года, прошедших со времени создания первого образца (С. Пател, 1964г.) их мощность в непрерывном режиме возросла от милливатта до многих киловатт. Сейчас выпускаются СО₂-лазеры с мощностью до 10 кВт, в том числе более 50 типов СО₂-лазеров с ВЧ-накачкой в диапазоне мощностей от 3 Вт до 5 кВт. При этом газовые лазеры с ВЧ-возбуждением обладают целым рядом преимуществ по сравнению с лазерами, в которых для накачки рабочей среды применяется самостоятельный тлеющий разряд постоянного тока. В частности, их конструкция и технология изготовления проще, а надёжность, ресурс работы, удельные характеристики существенно выше чем у лазеров с накачкой постоянным током. Это позволяет уменьшить габариты и массу технологических СО₂-лазеров мощностью ~1 кВт настолько, что становится возможным размещение такого лазера на подвижном манипуляторе промышленного робота.

       Сегодня известно большое количество различных конструкций газовых лазеров с ВЧ-возбуждением. Но в основе всего многообразия конструктивных решений лежит специфика пространственной структуры ВЧЕР, которая в большинстве случаев удачно совпадает с требованиями, предъявляемыми к активной среде лазера.

 

Квантовое описание лазера

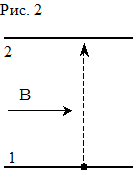
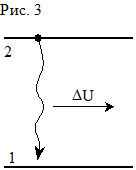
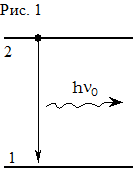       Возбуждённая частица может перейти в менее энергетическое состояние самопроизвольно в результате спонтанного излучения, или, как его ещё называют, радиационного распада (рис. 1). Спонтанное излучение имеет чисто квантовую природу. Согласно квантовой механике атом или молекула не могут находиться в возбуждённом состоянии бесконечно долго. 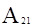Возбуждённое состояние распадается с конечной скоростью, определяемой вероятностью этого перехода в единицу времени , испуская при этом квант света с энергией hn₀=e₂-e₁   А(2)®А(1)+ hn₀  (  - коэффициент Эйнштейна для спонтанных переходов). Изменение концентрации частиц N₂ на верхнем уровне в результате спонтанных переходов описывается выражением 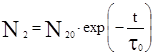. Кванты света, родившиеся в результате спонтанных переходов обладают одинаковой энергией но никоим образом не связаны между собой. Направления распространения этих квантов в пространстве равновероятны. Так как рождение кванта может с равной вероятностью произойти в любой момент времени, электромагнитные волны, соответствующие этим квантам, не связаны между собой по фазе и имеют произвольную поляризацию.

    В отличие от спонтанных переходов, способных происходить в изолированной частице, безизлучательные переходы возможны только при наличии взаимодействия частицы А с другой частицей или системой частиц В. В результате такого взаимодействия частица переходит из состояния 1 в состояние 2 или наоборот без излучения кванта света и без его участия. Процесс столкновительного возбуждения (рис.2) требует затраты кинетической энергии 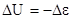 и протекает по схеме А(1)+В®А(2)+В. Процесс столкновительной релаксации на (рис.3) наоборот сопровождается переходом энергии  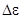в поступательную энергию взаимодействующих частиц либо тратится на возбуждение частицы В. Этот переход происходит по схеме A(2)+B®A(1)+B+ . Индуцированные, или, как их иногда называют, вынужденные переходы в соответствии с гипотезой А. Эйнштейна могут происходить только при взаимодействии частицы А с резонансными квантами, удовлетворяющими условию hn₀=e₂-e₁ т.е вероятность индуцированных переходов отлична от нуля лишь во внешнем электромагнитном поле с резонансной частотой n₀. А. Эйнштейн предположил, что при наличии поля резонансной частоты помимо переходов 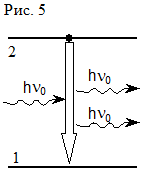квантовой системы из состояния 1 в состояние 2, что соответствует резонансному поглощению квантов, протекающему по схеме А(1)+hn₀®A(2) (рис.4) возможны переходы по схеме А(2)+hn₀®А(1)+2hn₀ (рис.5). Данный процесс индуцирования или вынужденного излучения и служит основой квантовой электроники.

Однако энергия возбуждённых состояний не является фиксированной величиной даже в случае изолированной частицы. Согласно принципу неопределённости Гейзенберга неточность в определении энергии системы и времени её существования должна удовлетворять соотношению: . Поскольку 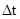~t₀ то неопределённость энергии возбуждённого состояния составляет 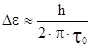. Такое энергетическое размытие уровней приводит к неопределённости частоты излучаемого кванта . Данное уширение частоты излучения называется естественная ширина линии и является минимально возможной. Естественная ширина линии резко растёт с ростом n (~n³) и становится заметной в коротковолновой части спектра. Для основного перехода молекулы СО₂ лазера t₀»5 сек и ширина n₀»3*10^-2 Гц. Однако обычно ширина линии излучения определяется не спонтанным излучением а релаксационными безизлучательными переходами, происходящими при взаимодействии возбуждённой частицы с другими частицами. Любой релаксационный процесс приводит к сокращению времени жизни частицы в возбуждённом состоянии, а следовательно, к уширению соответствующей этому состоянию линии излучения. Релаксационное уширение происходит за счёт безизлучательных процессом при столкновении частиц и этот процесс называют столкновительное уширение. По аналогии с естественный шириной линии, принимая t_cт - время жизни частицы в возбуждённом состоянии столкновительное уширенение определяется как 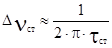. Время жизни частицы определяется через сечение этих процессов t_ст  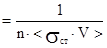Как правило возбуждённая частица взаимодействует с различными частицами и в общем случае t_{ст 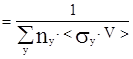,} где суммирование проводится по всем видам взаимодействующих частиц. Столкновительное и естественное уширение вызвано одной той же причиной – конечным временем жизни частицы в возбуждённом состоянии. Форма линии уширения в обоих случаях определяется особенностью вероятностных процессов и поэтому одинакова. Она имеет так называемый лоренцев контур, описываемый форм-фактором . Выражение нормировано на единицу: . Уширение линии, связанное с конечностью времени жизни возбуждённого состояния, принято называть однородным. В случае однородного уширения каждая возбуждённая частица при переходе излучает линию с полной шириной , спектральной формой 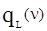 и поглощает кванты с частотой, лежащей в пределах контура 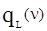. При однородном уширении форма линии описывает спектральные характеристики каждой частицы и всех частиц в целом. Но конечное время жизни частиц не является единственной причиной уширения линий. Излучающие частицы находятся, как правило, в тепловом движении. В соответствии с эффектом Доплера частота, испускаемая движущимся источником колебаний, претерпевает смещение, пропорциональное скорости движения излучателя V. Смещение частоты зависит также от угла j между направлением движения и линией, соединяющей излучатель с приёмником и составляет 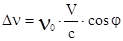. Так как излучающие частицы движутся с различными скоростями и в различных направлениях, то частотные сдвиги излучаемых ими линий различны. Поэтому даже в случае отсутствия столкновений неподвижный спектральный прибор будет регистрировать множество естественно уширенных линий, различно смещённых относительно частоты n₀. Суперпозиция этих смещённых линий и даёт наблюдаемый профиль уширённой линии. Это так называемое доплеровское уширение линии является неоднородным. Каждая частица в описанной ситуации может излучать линию лишь в узком, определяемом естественным уширением, спектральном диапазоне, сдвинутом относительно n₀ на конкретную величину, однозначно связанную со скоростью и направлением движения этой частицы. Естественно, что и поглощать излучение с фиксированной частотой смогут только те частицы, доплеровский сдвиг которых соответствует этой частоте. При максвелловском распределении излучающих частиц по скоростям  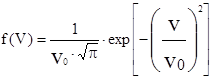где  - средняя тепловая скорость; m - масса частицы. При этом линия излучения имеет гауссов профиль, описываемый форм-фактором 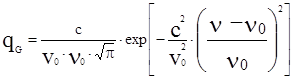  . Аналогично с  выражение нормировано на единицу .

В общем случае полная ширина линии излучения определяется всеми механизмами уширения. Однако в реальной ситуации чаще всего преобладающим является один. Это вызвано различным характером зависимост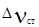и  и 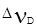 от внешних условий. Так, например, в случае газовой излучающей среды  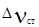линейно растёт с концентрацией частиц, а  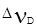зависит только от температуры. Поэтому при малых давлениях уширение будет определяться доплеровским эффектом, а при больших - столкновениями. Спектральное распределение излучаемой линии имеет вид симметричной резонансной кривой (рис.6) с максимумом на частоте n=n₀, спадающей до уровня половины максимальной интенсивности при частотах

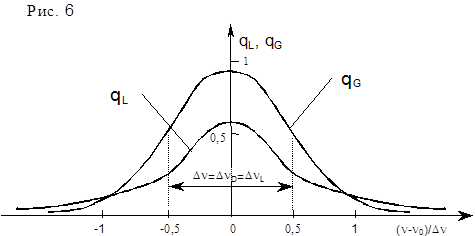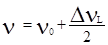. Наличие уширения энергетических уровней и излучаемых линий, не влияя на интегральную частоту вынужденных переходов, приводит к уменьшению вероятности переходов с конкретной длиной волны. Т.к. линия излучения имеет спектральную форму q(n), то вероятность спонтанного излучения с заданной частотой будет определяться полной вероятностью соответствующих переходов А₁₂ и видом форм-фактора q(n) т.е. W_сп(n)=А₂₁*q(n) где W_сп(n)- вероятность спонтанного излучения. Вероятности спонтанного и вынужденных переходов связаны между собой, поэтому вероятность индуцированных излучения с заданной частотой W₂₁(n) также зависит от n: W₂₁(n)=B₂₁*q(n)*s_V, B₂₁ – коэффициент Эйнштейна для индуцированного излучения,  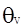– спектральная объёмная плотность излучения. Интегральная вероятность индуцированного излучения W₂₁ при этом удовлетворяет условию 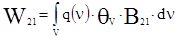. Для лоренцева вида линии форм-фактора такое интегрирование даёт , для гауссова 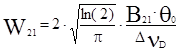, , 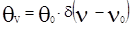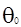- объёмная плотность излучения, d - дельта-функция. Сечение вынужденного фотоперехода для столкновительного уширения имеет вид: 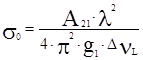, для доплеровской формы линии , g₁ – статистический вес уровня. Сечение вынужденного излучения s₂₁=s₀*g₁, вынужденного поглощения s₁₂=s₀*g₂. Процессы индуцированного излучения сопровождаются усилением электромагнитных волн. Пусть через среду, в которой частицы могут находиться в состояниях 1 и 2 с энергиями возбуждения e₁ и e₂ проходит поток монохроматического излучения удовлетворяющего соотношению hn₀=e₂-e₁. Пусть плотность частиц в этих состояниях N₁ и N₂. Уравнение баланса плотности фотонов в пучке имеет вид: 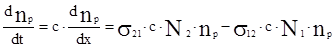 где n_p – объёмная концентрация фотонов. 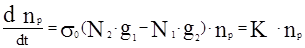. Величину  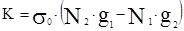называют коэффициентом активной среды. Интенсивность света будет усиливается по мере прохождения через среду с К>0. В противном случае при К<0 будет иметь место ослабление интенсивности изучения. Знак К определяется знаком выражения (N₂*g₁-N₁*g₂), называемого инверсией среды. Усиление среды положительно только лишь при (N₂*g₁-N₁*g₂)>0. В среде с термическим равновесием, где N₁ и N₂ подчиняются распределению Больцмана и где N₂ всегда меньше N₁, усиление света невозможно. Таким образом, усиление света может иметь место лишь при отсутствии термодинамического равновесия между уровнями 2 и 2, т.е. в неравновесной среде. Среду с N₂*g₁-N₁*g₂>0 называют средой с инверсной населённостью. Наилучшие условия резонансного излучения получаются при больших скоростях заселения и временах жизни верхнего уровня активных частиц и малых значениях этих величин для нижнего уровня.

Получение инверсной заселённости, состав активной среды, температурный режим, регенератор

В лазере на основе СО₂ используется четырёхуровневая система получения инверсной населённости между колебательными уровнями молекул. Молекула СО₂ состоит из атома углерода и двух симметрично расположенных атомов кислорода, т.е. имеет линейную структуру О-С-О. Как видно из схемы на рис. 7 атомы кислорода могут совершать симметричные (мода n₁ОО) и несимметричные (асимметричные) (мода n₃ОО), а также  поперечные этому направлению так называемые деформационные колебания (мода n₂^LOO) - из-за наличия двух взаимно перпендикулярных направлений этот тип колебаний является дважды вырожденным. Употребляемые для описания состояния колебательно-возбуждённой молекулы квантовые числа n₁, n₂^L и n₃ характеризуют число квантов, соответствующих колебанию данного типа, _L указывает поляризацию деформированного колебания. Лазерный квант излучается при переходе из состояния 001 в 100 (цифры обозначают колебательные квантовые числа в модах n₁, n₂^L и n₃ соответственно). Возможен также переход 001®020 с длиной волны l=9.4 мкм, но он обычно гораздо слабее. Для получения оптимальных условий в рабочую смесь СО₂-лазера помимо углекислого газа добавляют азот и гелий.

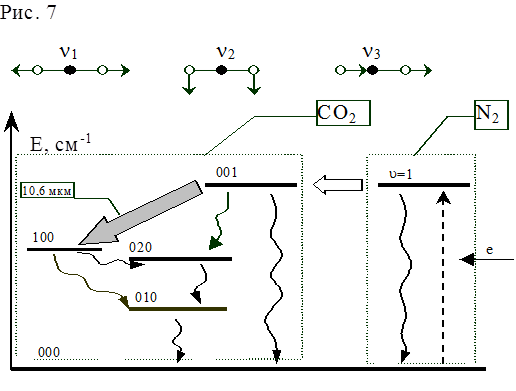Время жизни верхнего лазерного уровня СО₂ относительно спонтанных переходов составляет ~0.2 с (А₂₁»5.1 с^-1). Поэтому более интенсивно верхние и нижние лазерные уровни расселяются (релаксируют) в результате безизлучательных переходов при столкновениях возбуждённой молекулы с невозбуждёнными компонентами лазерной среды по схеме на рис. 3. Однако высокая эффективность получения инверсной заселённости в газоразрядных СО₂-лазерах обусловлена рядом причин. В электрическом разряде с высокой эффективностью образуются колебательно-возбуждённые молекулы N₂, составляющие до 50% их общего числа. Поскольку молекула N₂ состоит из двух одинаковых ядер, её дипольное излучение запрещено и она может дезактивироваться только при столкновении со стенкой или с другими молекулами. При наличии СО₂ колебательная энергия N₂ может быть легко передана молекулам СО₂ поскольку существует близкий резонанс между колебаниями N₂ и модой n₃ колебаний СО₂. Уровень 001 только на 18 см^-1 лежит выше первого колебательного уровня азота и необходимый недостаток энергии молекулы СО₂ могут получать от кинетической энергии азота. В результате энергия, затрачиваемая на возбуждение верхнего лазерного уровня и характеризуемая КПД разряда h_к, для смесей СО₂-N₂-He может превышать 80%. При наличии азота в смеси время релаксации, запасённой верхним уровнем энергии t_э увеличивается и становится равным . При средней плотности выделяемой в положительном столбе разряда мощности <jE>  заселённость верхнего лазерного уровня в отсутствии генерации будет . Создание инверсии требует малой населённости нижнего лазерного уровня. В условиях отсутствия генерации нижние уровни СО₂ находятся в тепловом равновесии с основным, их относительная заселённость ~ . Для поддержания стационарной генерации нижние уровни СО₂ необходимо расселять. Этот процесс обеспечивается добавлением в лазерную смесь расселяющих компонент, из которых наиболее эффективен гелий. Также помимо эффективного расселения уровня 100 гелий обеспечивает хороший теплоотвод от рабочей среды за счёт теплопроводности и оказывает стабилизирующее действие на заряд, поэтому в подавляющем большинстве существующих технологических лазеров предпочтение отдаётся ему. Таким образом, эффективная работа СО₂-ляазера требует трёхкомпонентной лазерной смеси. Определение состава рабочей среды лазера является сложной оптимизационной задачей, решение которой необходимо проводить в каждом конкретном случае. Для диффузионного СО₂-лазера часто используется смесь СО₂:N₂:He  в соотношении 1:1:3.

       Частотный спектр генерации СО₂-лазера имеет достаточно сложный вид. Причиной этого является наличие тонкой структуры колебательных уровней, обусловленной существованием ещё одной степени свободы молекулы СО₂ – вращения. Из-за вращения молекулы каждый изображённый на рис. 7 колебательный уровень распадается на большое количество вращательных подуровней, характеризуемых квантовым числом j и отстоящих друг от друга на величину энергии D e _вр, e ₀₀₁, e ₁₀₀, kT_r. В результате интенсивного обмена энергий между вращательной и поступательной степенями свободы устанавливается больцмановское распределение частиц по вращательным состояниям, описываемое уравнением 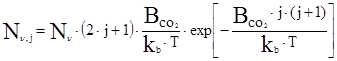, где N_n, N_n,j – концентрации возбужденных частиц на колебательном уровне n и на его вращательных подуровнях j; = 0,38 см^-1 – вращательная константа. Согласно правилам отбора в молекуле СО₂ переходы между двумя различными колебательными уровнями возможны при изменении вращательного квантового числа на 1 т.е. Dj=±1. Таким образом, линия усиления рабочей среды состоит из большого числа линий, каждая из которых уширена за счёт эффекта Доплера на величину  и за счёт столкновений на величину  и для СО₂-лазера вычисляются: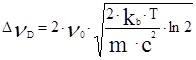  

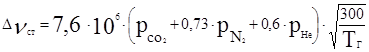, где р_i – парциальные давления компонент смеси.

       Коэффициент усиления активной среды СО₂-лазера существенно зависит от температуры рабочей смеси Т_г. Процессы накачки лазерной смеси и генерации неизменно сопровождается нагревом газа. Температура лазерной смеси Т_г в установившемся состоянии пропорциональна мощности энерговыделения в разряде, т.е. Т_г~jE. В отсутствие генерации заселенность верхнего лазерного уровня также пропорциональна jE. Поэтому если время столкновительной релаксации 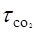 не зависит от температуры газа и N₀₀₁~Т_г, учёт возрастания  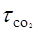с ростом Т_г лишь ослабит зависимость N₀₀₁(Т_г) (пунктирная линия). Заселённость нижнего лазерного уровня находится в равновесии с основным и описывается законом Больцмана N₁₀₀~ . В связи с этим при достижении некоторой критической температуры Т_max инверсная заселённость лазерной смеси исчезает. Максимальная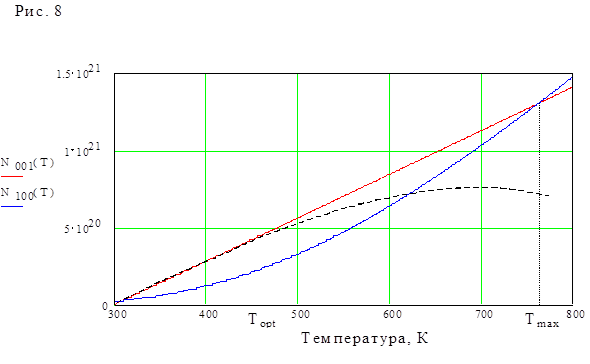
инверсия достигается при оптимальных температурах смеси Т_орt. Для смеси с c_г»1,5*10^-1 Вт/(м*К), Т_стенки»300К зависимость населённости лазерных уровней от температуры показана на рис. 8. Типичные значения Т_opt~400...500К, Т_мах~700...800К.

       Под действием электронных ударов и в результате столкновений возбуждённых молекул в тлеющем разряде в СО₂-лазерах происходит частичная диссоциация углекислого газа СО₂ ® СО + О. Отношение концентраций СО к СО₂ может достигать ~12%, содержание О₂ – 0,8%. Из-за этого при сохраняющемся энерговкладе возрастают потери на диссоциацию, возбуждение электронных состояний и возбуждение колебаний СО и О₂. Поэтому населённость верхнего рабочего уровня СО₂ падает и коэффициент усиления уменьшается. Поскольку ресурс работы СО₂-лазера, определенный требованиями экономичности установки, оценивается несколькими сотнями часов, а существенный рост доли СО и О₂ определяется минутами, необходимо включение в контур регенератора, в котором частично восстанавливается рабочая смесь. В диффузионном СО₂-лазере целесообразно применение цеолита (SiO₄+AlO₄) в количестве 20мг, насыщенного парами H₂O.

4. Резонатор

       Резонатор является оптической системой, позволяющей сформировать стоячую электромагнитную волну и получить высокую интенсивность излучения, необходимую для эффективного протекания процессов вынужденного излучения возбуждённых частиц рабочего тела лазера, а следовательно, когерентного усиления генерируемой волны. Оптические резонаторы в квантовой электронике не только увеличивают время жизни кванта в системе и вероятность вынужденных переходов, но и так же, как резонансные контуры и волноводы определяют спектральные характеристики излучения.

       В длинноволновом диапазоне классической электроники длина волны излучения существенно больше размеров контура и его спектральные характеристики определяются сосредоточенными параметрами электрической цепи. Длинные радиоволны при этом излучаются в пространство практически изотропно. При сокращении длины волны и переход в СВЧ-диапазону для формирования электромагнитной волны используются пустотелые объёмные резонаторы с размерами, сравнимыми с длиной волны. При этом появляется возможность формирования направленных (анизотропных) распределений излучения в пространстве с помощью внешних антенн. В ИК и видимом диапазоне длина волны излучения много меньше размеров резонатора. В этом случае оптический резонатор определяет не только частоту, но и пространственные характеристики излучения.

       Простейшим типом резонатора является резонатор Фабри-Перо, состоящий из двух параллельных зеркал, расположенных друг от друга на расстоянии L_p. В технологических лазерах резонатор Фабри-Перо используется крайне редко из-за больших дифракционных потерь. Чаще используются резонаторы с одной или двумя сферическими отражающими поверхностями. Свойства этих резонаторов зависят от знака и величины радиуса их кривизны R, а также от L_p и определяются стабильностью существования в нём электромагнитной волны.

       В так называемом устойчивом (стабильном) резонаторе распределение поля воспроизводится идентично при многократных проходах излучения между зеркалами и имеет стационарный характер. В результате попеременного отражения электромагнитных волн от зеркал волна формируется таким образом, что в приближении геометрической оптики не выходит за пределы зеркал в поперечном направлении и выводится из устойчивого резонатора только благодаря частичному пропусканию самих отражающих элементов. В случае отсутствия потерь, излучение могло бы существовать в устойчивом резонаторе бесконечно долго. В неустойчивом (нестабильном) резонаторе световые пучки (или описывающие их электромагнитные волны) в результате последовательных отражений от зеркал перемещаются в поперечном оси резонатора направлении к периферии и покидают его.

       Свойства резонаторов и характеристики создаваемых ими пучков можно описывать и в волновом, и в геометрическом приближении. В качестве критерия применимости этих приближений удобно использовать так называемое число Френеля 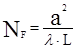, где a, L – характерные размеры задачи поперёк пучка и вдоль направления его распространения. Условие N_F>>1 соответствует применимости геометрического приближения. При N_F£1 необходимо учитывать также волновые свойства электромагнитного излучения.

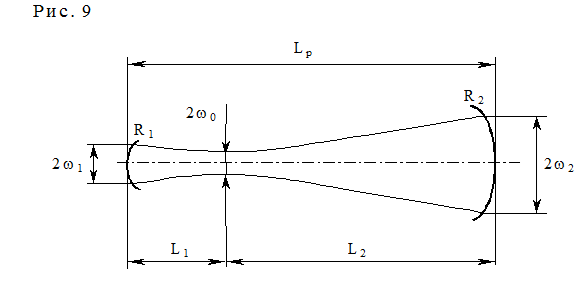
       В геометрическом приближении условие устойчивости резонатора имеет вид: 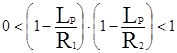. Расстояние между зеркалами L_p в этом выражении всегда положительно, а R₁ и R₂ положительны только для вогнутых т.е. фокусирующих зеркал и отрицательны для зеркал с выпуклой поверхностью. Для устойчивых резонаторов существует стационарное распределение интенсивности электромагнитного поля. В общем случае интенсивность излучения в устойчивых резонаторах распределена не равномерно по всему объёму резонатора, а сосредоточена внутри области, называемой каустикой (рис.9). Радиусы w₁, w₂, этой области на зеркалах а также её минимальный радиус w₀ в месте перетяжки определяются длиной волны и параметрами резонатора (R₁, R₂, Lp). Для основного типа колебаний их можно рассчитать с помощью соотношений: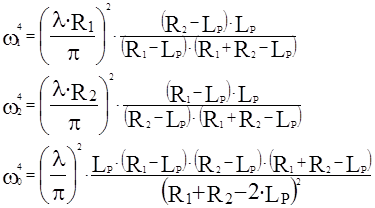

Расстояния L₁ L₂ от места положения перетяжки до зеркал составляют:          .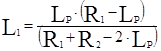

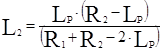       Наибольшее распространение получил среди устойчивых резонаторов полуконфокальный резонатор, у которого одно зеркало плоское (R₂=¥) а второе имеет радиус R₁=2L_P т.е. его фокус лежит на плоском зеркале. Основное удобство полуконфокального резонатора, определяющее его широкую распространённость, заключается в возможности использования для вывода излучения плоских окон из частично прозрачных материалов а также в параллельности выходящего пучка. В случае использования металлических зеркал излучение можно выводить через одно из них или систему отверстий.

       Устойчивый резонатор сравнительно прост в эксплуатации. Он легко юстируется, достаточно устойчив по отношению в разъюстировке. Его сферические зеркала сравнительно просто поддаются изготовлению и контролю радиуса кривизны. Поэтому они находят широкое применение в лазерной технике, особенно в технике маломощных (£ 1 кВт) лазеров. К числу недостатков устойчивых резонаторов следует отнести несовпадение объёма каустики с объёмом активной среды, что приводит к уменьшению КПД и увеличению размеров лазера, а также повышенные значения плотности мощности при перетяжке, что в случае её малых размеров может привести к оптическому пробою. Однако самым серьёзным недостатком устойчивых резонаторов является невысокая лучевая стойкость используемых в качестве выходных окон диэлектрических оптических материалов. Именно это обстоятельство ограничивает использование устойчивых резонаторов при больших плотностях излучения.

       В лазерах повышенной мощности в последнее время широкое распространение получили неустойчивые резонаторы со сферическими металлическими зеркалами. Наиболее часто в лазерной технике используется телескопический конфокальный неустойчивый резонатор, дающий на выходе параллельный пучок. Одно из его зеркал выпуклое, а другое вогнутое. Генерация возникает в приосевой зоне. Покидающее эту зону излучение усиливается при многократных проходах между зеркалами, смещаясь к периферии резонатора. Относительная величина смещения положения луча на выпуклом зеркале за один проход называется коэффициентом увеличения резонатора 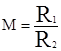. В отличие от устойчивого резонатора прозрачность неустойчивого резонатора определяется не пропусканием излучения выходным зеркалом, а геометрическими размерами системы. Из-за геометрического расширения излучения его интенсивность падает на одном проходе в М² раз. Однако в стационарных условиях при малых внутрирезонансных потерях усиление излучения на одном проходе также составит М². Таким образом, весь неустойчивый резонатор заполнен излучением с практически равной интенсивностью, что в отличие от устойчивых резонаторов обеспечивает полное и равномерное использование всей активной среды. Если добавить к этому высокую лучевую стойкость металлических зеркал, то преимущество неустойчивых резонаторов для мощных лазерных систем становится очевидным.

12	Поделиться:

Воспользуйтесь поиском по сайту: