 |
Кинетика мономолекулярных реакций в плотных средах
|
|
|
|
Ю.М.Буров, Институт проблем химической физики РАН, Черноголовка.
Мономолекулярные гомолитические реакции в газах, жидком и твердом состояниях рассмотрены в рамках модели свободного объема как объемно-активированные процессы. В рамках одного механизма описаны такие явления, как зависимость константы скорости реакции от внешнего давления и свойств растворителя, изменение ее при переходе газ-жидкость-твердое, влияние полиморфных переходов. Для газов теория Эванса-Поляни и предлагаемая теория дают близкие результаты, в растворах объемы активации, рассчитанные по предлагаемой теории, в 4-6 раз выше, чем вычисленные по традиционной теории. Показано, что для реакций с отрицательным объемом активации должна наблюдаться параболическая зависимость логарифма константы скорости от давления.
Кинетика реакций в плотных средах имеет ряд особенностей по сравнению с газофазной. Так как при образовании активированного комплекса (АК) происходит изменение формы и размеров молекулы, то наличие соседних молекул может этому препятствовать. На макроскопическом уровне это приводит к зависимости константы скорости реакции (k) от давления, агрегатного состояния вещества и полиморфных переходов, т.е. от плотности среды.
Традиционно эта проблема рассматривается в рамках теории Эванса-Поляни [1], впервые предложенной Вант-Гоффом [2], следующим образом. При образовании АК исходный объем молекулы Vo изменяется на величину объема активации 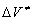 . Для деформации среды на эту величину требуется затратить дополнительную энергию D Е, на которую и увеличивается энергия активации реакции Е. Для реакций в жидком состоянии, в растворах [1]
. Для деформации среды на эту величину требуется затратить дополнительную энергию D Е, на которую и увеличивается энергия активации реакции Е. Для реакций в жидком состоянии, в растворах [1]
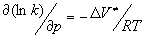 , (1)
, (1)
|
|
|
где p- внешнее давление, R - универсальная газовая постоянная. Аналогично рассматриваются и реакции в кристалле [3]. В этом случае дополнительная энергия D Е равна энергии упругой деформации кристалла на величину 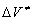 , т.е.
, т.е.  , где
, где  - сжимаемость вещества. В этом подходе вещество рассматривается как непрерывная среда, обладающее единственным свойством – передавать внешнее давление. Своего рода эфир физики XIX века. Молекулярная структура вещества никак не учитывается, что и проявляется в расхождении этой теории с опытом. Действительно, из уравнения (1) следует, что величина эффекта пропорциональна давлению и никакие свойства вещества на него не влияют. Но известно [4], что зависимость
- сжимаемость вещества. В этом подходе вещество рассматривается как непрерывная среда, обладающее единственным свойством – передавать внешнее давление. Своего рода эфир физики XIX века. Молекулярная структура вещества никак не учитывается, что и проявляется в расхождении этой теории с опытом. Действительно, из уравнения (1) следует, что величина эффекта пропорциональна давлению и никакие свойства вещества на него не влияют. Но известно [4], что зависимость 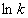 от давления, как правило, нелинейная, величина эффекта зависит от природы растворителя, температуры, давления. Поэтому в экспериментальных работах принято указывать используемый растворитель, температуру и диапазон давления, иногда величину
от давления, как правило, нелинейная, величина эффекта зависит от природы растворителя, температуры, давления. Поэтому в экспериментальных работах принято указывать используемый растворитель, температуру и диапазон давления, иногда величину 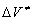 вычисляют экстраполяцией на p = 0.
вычисляют экстраполяцией на p = 0.
Причина этих противоречий, по-видимому, в том, что нельзя рассчитывать энергию деформации плотной молекулярной среды во время элементарного химического акта методами равновесной термодинамики. Для того, чтобы процесс был термодинамически равновесным, необходимо, чтобы характерные времена релаксации были много меньше времен, характеризующих внешнее воздействие на систему [5]. В действительности ситуация прямо противоположная. Времена внутримолекулярных перегруппировок порядка 10-13 с, а времена межмолекулярных движений порядка 10-8 – 10-10 с, т.е. время существования АК много меньше характерных времен межмолекулярных движений. Поэтому вместо модели, в которой молекула при образовании АК раздвигает среду, мы приходим к модели, в которой элементарный акт происходит на фоне практически неподвижного молекулярного окружения. Можно предложить следующую простую модель химической реакции в плотной среде. В веществе есть свободный объем 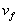 , некоторым образом распределенный по объему вещества. Если вблизи молекулы имеется готовая полость объемом
, некоторым образом распределенный по объему вещества. Если вблизи молекулы имеется готовая полость объемом  , в которой может поместиться АК, то реакция происходит с константой скорости
, в которой может поместиться АК, то реакция происходит с константой скорости 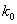 , если АК больше
, если АК больше 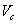 , то реакция не происходит, то есть
, то реакция не происходит, то есть  , где
, где  - вероятность образования полости размером
- вероятность образования полости размером  .
.
|
|
|
Таким образом, мы свели задачу о влиянии на константу скорости мономолекулярной химической реакции высокого давления, кристаллического состояния, полиморфных переходов к задаче определения свободного объема в различных условиях.
Известно, что в газах, жидкостях [6] и полимерах [7] свободный объем может флуктуировать без затрат или выигрыша энергии, чисто комбинаторно, и  , отсюда
, отсюда
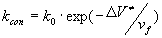 (2)
(2)
Для газов и жидкостей [8]
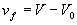 , (3)
, (3)
где V - мольный объем, т.е. 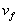 - это объем вещества, не занятый молекулами. В качестве k0 могут быть использованы kgas или kl при p =1атм..
- это объем вещества, не занятый молекулами. В качестве k0 могут быть использованы kgas или kl при p =1атм..
Рассмотрим конкретные примеры. В идеальном газе  , откуда
, откуда
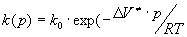 ,
,
то есть традиционная теория о влиянии высокого давления на скорость химической  реакции справедлива для идеального газа. Этот несколько странный результат может быть понят, если учесть, что для N точек, произвольно расположенных в объеме V, вероятность не попасть в
реакции справедлива для идеального газа. Этот несколько странный результат может быть понят, если учесть, что для N точек, произвольно расположенных в объеме V, вероятность не попасть в 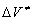 -окрестность i-той точки равна
-окрестность i-той точки равна  и
и 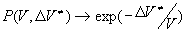 при
при  .
.
В ван-дер-ваальсовском газе уравнение состояния вещества 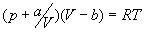 , причем
, причем 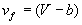 .
.
В [9] была изучена мономолекулярная реакция термораспада этилциклобутана в атмосфере азота при давлении до ~ 200 атм. и температуре 410o С. Объем активации, оцененный из предполагаемой геометрии АК, равен +21 см3 /моль, вычисленный по данным работы [9] (в самой работе [9]  вычислен неточно) из зависимости
вычислен неточно) из зависимости 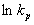 по уравнению (1) равен
по уравнению (1) равен  = +34,8±5,0 см3/моль. Для расчетов объема активации
= +34,8±5,0 см3/моль. Для расчетов объема активации  в модели свободного объема по уравнению состояния азота был рассчитан
в модели свободного объема по уравнению состояния азота был рассчитан  и построена зависимость
и построена зависимость 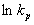 от
от 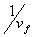 . Тангенс угла наклона этой зависимости, равный +36,8±5,0 см3/моль есть
. Тангенс угла наклона этой зависимости, равный +36,8±5,0 см3/моль есть  . Различие с традиционной теорией мало, лежит в пределах ошибки эксперимента. Это согласуется с тем, что свойства азота при этих температурах и давлениях близки к свойствам идеального газа.
. Различие с традиционной теорией мало, лежит в пределах ошибки эксперимента. Это согласуется с тем, что свойства азота при этих температурах и давлениях близки к свойствам идеального газа.

Влияние высокого давления на скорость реакции в растворе - это область кинетики, наиболее изученная экспериментально. Обзор [10] содержит данные о примерно 500 реакций, из них 22 относятся к мономолекулярным.
|
|
|
Для анализа экспериментальных данных методом теории свободного объема необходимо иметь уравнение состояния растворителя, включающее области температуры и давления, использованные в экспериментах. Часто это затруднительно. Справочник [11] содержит табулированные уравнения состояния для ряда жидкостей в диапазоне давлений до 500 атм. Для некоторых жидкостей имеются зависимости V(p) для отдельных значений температур, часто эти температуры лежат в стороне от температур, необходимых для исследования химической кинетики.
В качестве примера рассмотрим мономолекулярную реакцию с 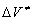 = 40 см3/моль в бензоле при температурах 350К, 475К и 575К (закритическая температура). Для бензола V0 = 53 см3/моль, определен методом инкрементов [12]. По уравнению (2) рассчитаем зависимость
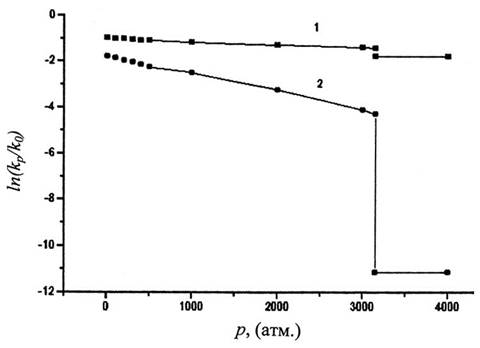
= 40 см3/моль в бензоле при температурах 350К, 475К и 575К (закритическая температура). Для бензола V0 = 53 см3/моль, определен методом инкрементов [12]. По уравнению (2) рассчитаем зависимость  от p. Нa рис.1 видно, что при переходе от газа к жидкости скорость реакции уменьшается (в 2,62 раза при 350К и в 1,85 раза при 475К). При 575К зависимость
от p. Нa рис.1 видно, что при переходе от газа к жидкости скорость реакции уменьшается (в 2,62 раза при 350К и в 1,85 раза при 475К). При 575К зависимость  при малых р нелинейная, и только при
при малых р нелинейная, и только при  бар, когда свойства бензола становятся близкими к свойствам жидкости, эта зависимость становится линейной. Вычисленные по уравнению (1)
бар, когда свойства бензола становятся близкими к свойствам жидкости, эта зависимость становится линейной. Вычисленные по уравнению (1)  равны 7,2 (350К), 16,8 (475К) и 24,5 (575К) см3/моль, т.е.
равны 7,2 (350К), 16,8 (475К) и 24,5 (575К) см3/моль, т.е.  меньше истинного в 2- 6 раз и возрастает с увеличением температуры.
меньше истинного в 2- 6 раз и возрастает с увеличением температуры.
Иногда предлагается разделить свободный объем, определенный по уравнению (3) на объем, образованный в результате термического расширения - VE, и недоступный объем - Vv. Для анализа этой проблемы построим зависимость  в бензоле при 80оС для
в бензоле при 80оС для 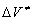 = 40 см3/моль в более широком интервале давлений, причем в уравнении (2) используем как
= 40 см3/моль в более широком интервале давлений, причем в уравнении (2) используем как 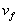 , так и VE.
, так и VE.
На рис.2 показана изотерма бензола при Т = 80oС. От 1 до 500 атм. она построена по табличным данным [11] и продлена для давлений р>500 атм. по уравнению Тэйта в виде [13]  , А = 0,0938, pcr = 48,6 атм., Тcr=562,65К, Vst - объем при pst =500 атм., параметр
, А = 0,0938, pcr = 48,6 атм., Тcr=562,65К, Vst - объем при pst =500 атм., параметр  =8,5.10-3 пересчитан мной по методу [13], поскольку в [13] эти параметры приведены с ошибкой почти в три порядка.
=8,5.10-3 пересчитан мной по методу [13], поскольку в [13] эти параметры приведены с ошибкой почти в три порядка.

При р=1 атм. vf= 41 см3/моль, a VE =18,4 см3/моль. При р=3125 атм. чистый бензол затвердевает со скачкообразным уменьшением объема на DVs,l =5,7 см3/моль [15]. Эта величина составляет при р = 1 атм. 6% от V(1), 14% от vfи 32% от VE.
|
|
|
 Из рис.3 видно, что зависимость
Из рис.3 видно, что зависимость  от p, построенная с использованием VE, намного круче, чем для кривой, построенной с использованием vf. Объем активации
от p, построенная с использованием VE, намного круче, чем для кривой, построенной с использованием vf. Объем активации  , вычисленный по уравнению (1), равен 30,3 см3/моль для первой кривой и только 7,2 см3/моль для второй кривой. Особенно различно их поведение в области затвердевания бензола. Если у второй кривой величина скачка
, вычисленный по уравнению (1), равен 30,3 см3/моль для первой кривой и только 7,2 см3/моль для второй кривой. Особенно различно их поведение в области затвердевания бензола. Если у второй кривой величина скачка  незначительна и лежит в пределах точности кинетических экспериментов, то на первой кривой величина торможения при переходе от жидкого состояния к твердому, так называемый ТЭР = 665. Это чрезвычайно высокое значение. Согласно [15], такой ТЭР могут иметь вещества с температурой плавления tm порядка 2000С. Для бензола, имеющего при атмосферном давлении tm= 5,5530С [14], ТЭР должен быть порядка 1. Более того, в экспериментах над реакциями в растворах не наблюдались скачки скорости при затвердевании растворителя под действием давления, хотя следует заметить, что специально такие эксперименты не ставились. В настоящий момент представляется, что использование vf в уравнении (2) более обосновано, чем использование VE.
незначительна и лежит в пределах точности кинетических экспериментов, то на первой кривой величина торможения при переходе от жидкого состояния к твердому, так называемый ТЭР = 665. Это чрезвычайно высокое значение. Согласно [15], такой ТЭР могут иметь вещества с температурой плавления tm порядка 2000С. Для бензола, имеющего при атмосферном давлении tm= 5,5530С [14], ТЭР должен быть порядка 1. Более того, в экспериментах над реакциями в растворах не наблюдались скачки скорости при затвердевании растворителя под действием давления, хотя следует заметить, что специально такие эксперименты не ставились. В настоящий момент представляется, что использование vf в уравнении (2) более обосновано, чем использование VE.
Для сравнения результатов, полученных по уравнению (1) и (2) обозначим объем активации в уравнении (1) как  , а в уравнении (2) как
, а в уравнении (2) как  . Эти объемы активации при р®1атм. относятся как
. Эти объемы активации при р®1атм. относятся как
 ,
,
где V(0) и  – соответственно, мольный объем и сжимаемость при р®1атм. Величина
– соответственно, мольный объем и сжимаемость при р®1атм. Величина  может быть рассчитана, например, по методу Рао [16,17], групповые инкременты, необходимые для этих расчетов, содержатся в [18]. Таким образом, расчеты по теории Эванса-Поляни дают для объемов активации в растворах величины, в 2? 6 раз меньшие, чем дает теория свободного объема.
может быть рассчитана, например, по методу Рао [16,17], групповые инкременты, необходимые для этих расчетов, содержатся в [18]. Таким образом, расчеты по теории Эванса-Поляни дают для объемов активации в растворах величины, в 2? 6 раз меньшие, чем дает теория свободного объема.
В настоящее время отсутствуют надежные экспериментальные данные по величинам  начальных, мономолекулярных стадий реакций в твердых органических веществах в широком интервале давлений, достаточном для определения влияния давления на константу скорости начальной, мономолекулярной стадии реакции. В экспериментах по влиянию высокого давления на процессы теплового воспламенения или на зажигание ВВ исследуются глубокие, автокаталитические стадии химического процесса, и потому вычисленные в этих работах
начальных, мономолекулярных стадий реакций в твердых органических веществах в широком интервале давлений, достаточном для определения влияния давления на константу скорости начальной, мономолекулярной стадии реакции. В экспериментах по влиянию высокого давления на процессы теплового воспламенения или на зажигание ВВ исследуются глубокие, автокаталитические стадии химического процесса, и потому вычисленные в этих работах  не относятся к начальным, мономолекулярным стадиям. Однако существует интересное явление, состоящее в резком снижении скорости мономолекулярных реакций в органических веществах при переходе от жидкого состояния к твердому [3,19-21]. Для ряда веществ ТЭР может превосходить 10000. Известно, что при переходе вещества из одной кристаллической модификации в другую скорость химической реакции в нем изменяется. Эти явления могут быть описаны в рамках предлагаемой модели.
не относятся к начальным, мономолекулярным стадиям. Однако существует интересное явление, состоящее в резком снижении скорости мономолекулярных реакций в органических веществах при переходе от жидкого состояния к твердому [3,19-21]. Для ряда веществ ТЭР может превосходить 10000. Известно, что при переходе вещества из одной кристаллической модификации в другую скорость химической реакции в нем изменяется. Эти явления могут быть описаны в рамках предлагаемой модели.
|
|
|
При переходе от жидкого состояния к твердому, объем вещества уменьшается примерно на 10% [22]. Это приводит к уменьшению свободного объема и, соответственно, скорости реакции. Величина тормозящего эффекта решетки (ТЭР =  для разных веществ лежит в широком интервале от единиц до 104 [17]. Следует учитывать, что при ТЭР >103 реакция локализуется на неравновесных дефектах, дислокациях, границах зерен, поверхности, примесях, и потому истинный ТЭР может быть значительно выше.
для разных веществ лежит в широком интервале от единиц до 104 [17]. Следует учитывать, что при ТЭР >103 реакция локализуется на неравновесных дефектах, дислокациях, границах зерен, поверхности, примесях, и потому истинный ТЭР может быть значительно выше.
Для кристаллических веществ данное выше определение vf нуждается в уточнении. В рамках ячеечной модели Ленард-Джонса [23] свободный объем может быть рассчитан методом атом-атом потенциала [24]. Величину VEможно оценить по тепловому расширению  , где V0- мольный объем при 0 К, a (Т) - термический коэффициент расширения. Если a = const, то при V0 = 100 см3/моль и Т = 500 K VE равен 5 см3/моль при a= 10-4град-1 и 50 см3/моль при a= 10-3 град-1. Энергоемкие соединения, состоящие из полярных молекул, имеют a= (1 - 2,5).10-4 град-1, величина a» 10-3 град-1 характерны для парафинов [25]. В органических кристаллах от 20 до 36% вещества приходится на пустоты упаковки [25], т.е. на VV. Этот объем не является абсолютно недоступным. По-видимому, при удачном расположении реакционного центра относительно пустот упаковки, они могут быть использованы для создания Vc [21].
, где V0- мольный объем при 0 К, a (Т) - термический коэффициент расширения. Если a = const, то при V0 = 100 см3/моль и Т = 500 K VE равен 5 см3/моль при a= 10-4град-1 и 50 см3/моль при a= 10-3 град-1. Энергоемкие соединения, состоящие из полярных молекул, имеют a= (1 - 2,5).10-4 град-1, величина a» 10-3 град-1 характерны для парафинов [25]. В органических кристаллах от 20 до 36% вещества приходится на пустоты упаковки [25], т.е. на VV. Этот объем не является абсолютно недоступным. По-видимому, при удачном расположении реакционного центра относительно пустот упаковки, они могут быть использованы для создания Vc [21].
Объем активации в кристалле зависит от локального молекулярного окружения и может значительно отличаться от DV?, определенного в растворе, то есть Vc =  = g
= g 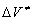 . Появление g > 1 можно пояснить на простом примере. Пусть молекула имеет форму шара и Vo =4/3pR3, а объем активации в виде полусферы с радиусом
. Появление g > 1 можно пояснить на простом примере. Пусть молекула имеет форму шара и Vo =4/3pR3, а объем активации в виде полусферы с радиусом 

 r?, равный
r?, равный 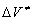 = 2/3 p (r?)3, расположен в точке касания молекул. Тогда
= 2/3 p (r?)3, расположен в точке касания молекул. Тогда  будет иметь форму цилиндра с радиусом R и высотой r? и g= 3/2(V0/2?
будет иметь форму цилиндра с радиусом R и высотой r? и g= 3/2(V0/2? 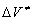 )2/3. Для DV?= 1; 5 и 10 см3/моль значения
)2/3. Для DV?= 1; 5 и 10 см3/моль значения  и g будут соответственно 33,6; 57,5 и 72,5 см3/моль и 33,6; 11,5; 7,25. В случае, если реакционный центр расположен так, что для образования АК могут быть использованы пустоты упаковки, то g может быть меньше 1. Примером такого соединения может служить 1,3-дифенилтриазен [26].
и g будут соответственно 33,6; 57,5 и 72,5 см3/моль и 33,6; 11,5; 7,25. В случае, если реакционный центр расположен так, что для образования АК могут быть использованы пустоты упаковки, то g может быть меньше 1. Примером такого соединения может служить 1,3-дифенилтриазен [26].
Пока не выяснено, можно ли применять уравнение (2) для кристаллов. Доводом в пользу его применимости может быть то, что аксиомы ячеечной модели более соответствуют кристаллам, а не жидкостям и газам, для которых она была первоначально предложена, и в рамках которой было введено понятие ”свободный объем” [24].
Если предлагаемая модель справедлива для молекулярных кристаллов, то для веществ, имеющих ТЭР = 104, отношение  должно быть 9,2 а для ТЭР = 10
должно быть 9,2 а для ТЭР = 10  =2,3. Несмотря на то, что в рассматриваемой модели свободный объем образует Vс без затрат или выигрыша энергии, чисто комбинаторно, тем не менее дополнительная энергия активации
=2,3. Несмотря на то, что в рассматриваемой модели свободный объем образует Vс без затрат или выигрыша энергии, чисто комбинаторно, тем не менее дополнительная энергия активации  появляется из-за температурной зависимости vf.
появляется из-за температурной зависимости vf.
В [27] было показано, что 1,3,5,7-тетранитро - 1,3,5,7 - тетраазациклооктан в различных полиморфных модификациях имеет различные скорости термораспада. Приняв коэффициент термического расширения для всех трех модификаций равным a= 1,4.10-4 град-1, получим оценки величин VT и DVs?(см. табл.).
В заключение рассмотрим влияние высокого давления на реакции с отрицательным объемом активации. Примером таких реакций могут служить реакции с циклическим АК. Поскольку характерные времена внутримолекулярных перегруппировок много меньше времен межмолекулярных движений, то химическая реакция происходит при неподвижном молекулярном окружении и потому влияние давления реализуется до начала молекулярной перегруппировки и состоит в упругой деформации молекулы по координате реакции. В результате энергия основного состояния молекулы увеличивается на величину, пропорциональную квадрату давления, соответственно на эту величину уменьшается энергия активации, что приводит к ускорению химической реакции. Так как молекулярное окружение одновременно тормозит внутримолекулярные движения по рассмотренному выше механизму, то суммарное влияние давления можно описать как 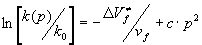 , где с> 0 - коэффициент, характерный для данной реакции. Так как первый член зависит от давления почти линейно, то зависимость может быть приближенно представлена в виде
, где с> 0 - коэффициент, характерный для данной реакции. Так как первый член зависит от давления почти линейно, то зависимость может быть приближенно представлена в виде
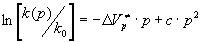 .
.
Следует заметить, что отсутствие внимания к влиянию на скорость реакции плотности вещества и акцентирование внимания на эффектах давления следует, видимо, из того, что при изменении давления в широком диапазоне от атмосферного до тысяч атмосфер плотность меняется незначительно, на несколько процентов.
Список литературы
1. Evans M.G., Polanyi M.//Trans. Faraday Soc. 1935. V.31. P. 875.
2. Van,t Hoff J.H. Lectures on Theoretical and Physical Chemistry. Braunschweig, 1901.
3. Манелис Г.Б. Некоторые особенности механизма реакций в твердой фазе// Проблемы кинетики элементарных химических реакций. М.: Наука. 1973.С.93.
4. Eckert C.A. Annual Review of Physical Chemistry, H.Eyring - Editor for University of Utah. 1972. V. 23. P. 239.
5. Ландау Л.Д., Лифшиц Е.М. Статистическая физика//Теоретическая физика. Т.5. С.56.
6. Бурштейн А.И. Молекулярная физика. Новосибирск: Наука. Сиб. отд- ние, 1986. C 128.
7. Cohen M.H., Turnbull D.// J. Chem. Phys. 1959 V. 31. P. 1164.
8. Глесстон С., Лейдлер К., Эйринг Г. Теория абсолютных скоростей реакций, ИЛ, М., 1948. [Glasstone S., Laidler K., Eyring H. The Theory of Rate Processes. NY and London. Frick Chemical Laboratory. Princeton University. 1941].
9. Asped J.// J. Am. Chem. Soc. 1969. V.91. P. 7580.
10. Asano T., le Noble W.J.// Chem. Rev. 1978. V. 78. N 4. P.407.
11. Справочник по теплофизическим свойствам газов и жидкостей. Ред. Варгафик Н.Б. М.: Наука. Издание второе. 1972.
12. Китайгородский А.И. Молекулярные кристаллы. М.: Наука. 1971. С.27.
13. Атанов Ю.А. // ЖФХ. 1966. Т. 140. С. 1216.
14. Справочник химика // Т.I. Издание 3-е. Ленинград. ”Химия”. 1971. C. 545.
15. Буров Ю.М., Манелис Г.Б., Назин Г.М.// Известия Академии наук. Сер. хим. 1999. № 7. С. 1260.
16. Rao M.R.//J. Chem. Phys. 1941.V.9. 682.
17. Столяров Орлова Расчет физико-химических свойств жидкостей. Ленинград.: “Химия”. 1976. С.72.
18. Воскобойников И.М. Афанасенков А.Н., Богомолов В.М.// Физика горения и взрыва. 1967. №3, С.585.
19. Бон С. //Химия твердого состояния. М.: ИЛ 1961. С.540. [Chemistry of the Solid State, Ed. Garner W.E. Butterworths. London. 1955] 20. Буров Ю.М., Манелис Г.Б., Назин Г.М.//Докл. АН СССР, 1984. Т.279. №. С.1142.
21. Манелис Г.Б., Назин Г.М., Рубцов Ю.И., Струнин В.А.//Термическое разложение и горение взрывчатых веществ и порохов. М.: Наука.1996. С.16.
22. Уббелоде А.Р. //Плавление и кристаллическая структура. М.:Мир, 1969. С. 20. [Ubbelohde A.R. Melting and Crystal Structure. Clarendone Press. Oxford. 1965].
23. Lennard-Jones J.E. // Proc. Phys. Soc. 1940. V. 52. P.729.
24. Китайгородский А.И.// УФН. 1979. Т.127. Вып.3. С.391.
25. Китайгородский А.И.//Молекулярные кристаллы. М.: Наука.1973. С.327.
26. Буров Ю.М. Кинетика реакции термического распада 1,3-дифенилтриазена. Черноголовка. 1984. Препринт.
27. Буров Ю.М., Манелис Г.Б., Назин Г.М. // Химическая физика. 1985. Т.4. N 7. С.956.
|
|
|


