Исследование переходных процессов в RLC – цепях

Лабораторная работа №4

Цель работы: исследование переходных процессов в RLC – цепях при воздействии прямоугольных импульсов напряжения.

Одним из методов исследования переходных процессов в электрических цепях является операторный метод /1,2/. При этом используется преобразование Лапласа:

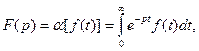(1)

определяющее изображение F(p) по известному оригиналу f(t).

Решение интегро-дифференциального уравнения цепи относительно искомой функции времени (оригинала) сводится к решению алгебраического уравнения для изображения.

 

1. RC - цепь

Пусть на вход цепи, схема которой приведена на рис.1,а, подается прямоугольный импульс напряжения. Требуется найти форму напряжения на входе цепи, Для этого необходимо выполнить следующие этапы вычислений:

1) записать аналитическое выражение входного сигнала;

2) составить интегро-дифференциальное уравнение цепи;

3) перейти к операторному уравнению;

4) решив операторное уравнение, найти изображение искомой функции;

5) перейти к оригиналу искомой функции.

Аналитическое выражение идеального прямоугольного импульса напряжения амплитуды E запишем в виде.

(2)

где l(t) – единичная функция, определяемая условиями:

l(t)=0, если t<0 и l(t)=1, если t>=0.

Выражение (2) представлено графически на рис.1,б. Для t>t_u разность единичных функций дает нуль. Уравнение цепи имеет вид

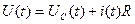(3)

где входное воздействие U(t) определяется выражением (2), U_R(t) и i(t) – напряжение на конденсаторе и ток в цепи в произвольный момент времени. Выходное напряжение U_R=i(t)R с точностью до множителя R совпадает с i(t), поэтому выберем i(t) в качестве искомой функции и учтем, что i(t)=dq(t)/dt=CdU_C(t)/dt. Тогда (3) с учетом (2) примет вид

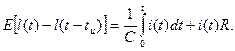(4)

Введем изображение тока I(p)=a[i(t)] и применим преобразование Лапласа (1) к обеим частям (4). С учетом изображения единичной функции и теоремы интегрирования оригинала операторное уравнение примет вид

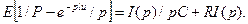(5)

Решение его

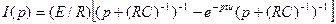(6)

Переход к оригиналу осуществляется также о помощью таблицы 1:

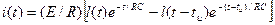(7)

 

 

Таблица 1

Некоторые свойства преобразования Лапласа

 

№ Свойство

п/п

 

1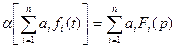

 

2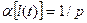

 

 

3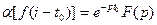

 

4

 

5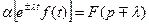

 

 

6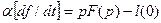

 

 

7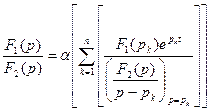

 

Графически зависимость (7) представлена на рис.1,в для случая t<<t_u, где t=RC. На рис.1, г представлена зависимость U_R(t).

Рассмотрим схему на рис.2,а. Для получения зависимости U_c(t) при входном воздействии (2) уравнение (3) представим так:

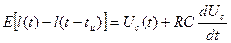(8)

Вводя изображение напряжения U_c(p)=a[U_c(t)], переходим с помощью табл.1 к операторному уравнению:

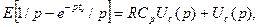(9)

где учтено, что U_c(0)=0. Решая (9) относительно U_c(p) и переходя к оригиналу, получим

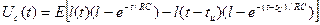(10)

Графически эта зависимость представлена на рис.2,в.

Таким образом, как следует из выражений (7) и (10) (см. рис1,в;1,г;2,в), передний и задний фронты входного П-импульса напряжения вызывают в RC-цепи переходной процесс. На переднем фронте происходит протяженный во времени заряд конденсатора (увеличение U_c(t)), а ток i(t) по мере заряда конденсатора уменьшается до нуля. При воздействии заднего фронта импульса начинается заряд конденсатора через резистор и источник входного сигнала. Ток при этом течет в противоположном направлении и постепенно уменьшается по абсолютной величине. С этим связано появление на осциллограмме отрицательного выброса U_R(t). Время переходного процесса, т.е. время, за которое конденсатор зарядится до напряжения источника E, теоретически бесконечно велико. На практике длительность переходного процесса в RC-цепях характеризуют постоянной времени t=RC, которая показывает, за какой промежуток времени ток в цепи уменьшается в e раз (из (7) при t=t i=0,367(E/R)) или - за какой промежуток времени напряжение на конденсаторе достигнет величины 0,633 E (из (10)) при t=t U_c=(1-e^-1)E=0,633E). При оценке t по осциллограмме U_c(t) следует выполнить условие t<<t_u, чтобы переходной процесс успевал заряжаться до напряжения E за промежуток времени t_u. Если указанное условие нарушено, то конденсатор не будет успевать заряжаться до напряжения E за промежуток времени t_u. В этом случае

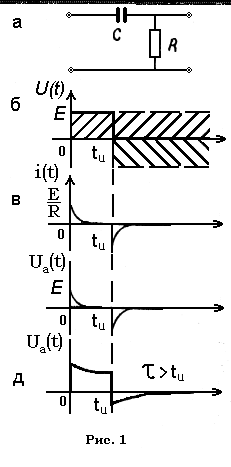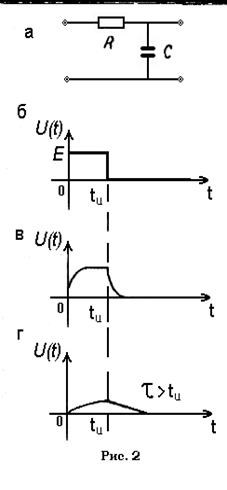осциллограммы U_R(t) и U_C(t) будут иметь вид, показанный на рис.1,д и 2,г.

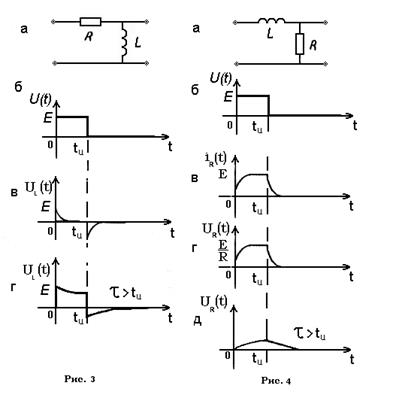
2. RL-цепь.

Рассмотрим RL-цепь, схема которой представлена на рис.3,а, для которой входное напряжение

U(t)=i(t)R+U_L(t) (11)

Или с учетом (2) и U_L(t)=L di(t)/dt

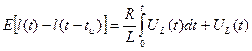(12)

Сравнивая (12) и (4), заметим, что эти уравнения совпадают при взаимной замене искомых функций и введении для RL- цепи постоянной времени t=R/L, поэтому решение (12) запишем по аналогии с (7):

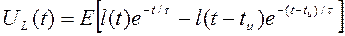(13)

где t=L/R. Форма напряжения U_L(t) для RL-цепи повторяет форму напряжения U_R(t) для RL-цепи (рис.3). Аналогично можно показать, что форма U_R(t) для RL-цепи повторяет форму U_C(t) для RC-цепи (рис.4). Для этого достаточно из (11) получить уравнение относительно l(t) и сравнить его с (8).

Переходной процесс в RL-цепи на переднем и заднем фронте входного импульса обусловлен протяженностью процесса накопления и рассеивания энергии магнитного поля в катушке.

В радиоэлектронике применяются цепи, напряжение на входе которых пропорционально производной или интегралу от входного напряжения. Такие цепи называются соответственно дифференцирующие или интегрирующими. Дифференцирующими являются цепи, схемы которых приведены на рис.1 и 3, если их постоянные времени достаточно малы (по сравнению с длительностью входного сигнала). Интегрирующими являются цепи, схемы которых показаны на рис 2. И 4, если их постоянные времени достаточно велики (по сравнению с интервалом интегрирования). Для этого выходное напряжение приходится выбирать существенно меньшим выходного.

3. RLC-цепь.

Рассмотрим цепь, схема которой представлена на рис.5,а. Для упрощения расчета рассмотрим воздействие на цепь положительной ступеньки напряжения, т.е. входное воздействие выберем в виде U(t)=E l(t). Тогда уравнение U(t)=U_R(t)+U_L(t)+U_C(t), записанное относительно U_C(t), примет вид

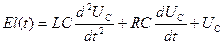(14)

Переходя к операторному уравнению относительно изображения и решая его, найдем

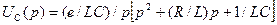(15)

 

Корни P_1,2=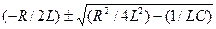

Уравнения p²+(r/L)p+1/LC=0, могут быть комплексными, вещественными(равными в частном случае), поэтому различают колебательный, апериодический и критический режим работы контура. При условии (l/LC)>R²/4L² имеем колебательный конур. Тогда, полагая p₁=-s ± jw, где s=R/2L – коэффициент затухания контура, 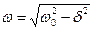- круговая частота свободных (собственных) колебаний, - резонансная частота контура, перепишем (15) так:

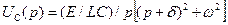(16)

Корни знаменателя в (16) простые, поэтому, применяя теорему разложения (см.табл.1) и считая затухание малым 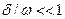, т.е. w=w_0, имеем

(17)

Тогда

(18)

(19)

Отсюда видно, что ток в цепи и напряжение на конденсаторе осциллируют, причем амплитуде осцилляций монотонно убывает, что характерно для переходного процесса в колебательном контуре.

 

4. Практическая часть

1. Ознакомится с оборудованием (генератор прямоугольных импульсов напряжения, осциллограф, макет).

2.Собрать RC-цепь. С помощью осциллографа просмотреть и зарисовать формы входного импульса напряжения и импульсов напряжения на резисторе и конденсаторе. По осциллограммам оценить постоянную времени цепи t и сравнить ее с произведением RC, где R C – номинальные значения параметров элементов.

3.Выполнить задание п.2 для случаев, когда на одну и ту же RC-цепь действует прямоугольные импульсы напряжения разной длительности и импульс с t_u=const действует на RC-цепь, постоянная времени которой изменяется за счет изменения как R, так и C. Рассмотреть случаи t<<t_u, t 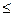t_u, t>t_u. Для случая t<<t_u построить графики зависимостей t(R) и t(C).

4. Выполнить задания пунктов 2 и 3 применимо к RL-цепям. Для случая t<<t_u построить графики зависимостей t(L) и t(1/R).

5. Собрать последовательную RLC-цепь. С помощью осциллографа просмотреть и зарисовать формы входного импульса напряжения и импульсов напряжения на элементах цепи. По осциллограммам напряжения на элементах цепи наблюдать переход от апериодического к колебательному при изменении коэффициента затухания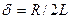

В колебательном режиме оценить период колебаний T и сопоставить его с вычисленным значением. Зарегистрировать зависимость T от емкости С при .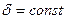

6. Обсудить полученные результаты.

5. Контрольные вопросы

1. Что такое переходной процесс в электрической цепи?

2. Как оценивают длительность переходного процесса?

3. Что такое постоянная времени электрической цепи?

4. Какими выражениями описываются зависимости напряжений на элементах RC и RL – цепей от времени, если входным воздействием являются прямоугольный импульс напряжения?

5. Как оценить постоянную времени электрической цепи по осциллограмме напряжения на элементе цепи?

6. Можно ли оценить t по осциллограмме рис.2,г, используя переходной фронт импульса?

7. Всегда ли одинаковы постоянные времени цепи, оцененные по переднему и заднему фронту импульса?

8. Какие физические процессы происходят в RC и RL –цепях при воздействии прямоугольного импульса напряжения?

9. Почему в RLC-цепи возникает колебательный процесс при прямоугольном импульсе на входе?

10. Как можно качественно объяснить осциллограммы l(t) и U_c(t) на рис.5?

11. Каким образом изменяются осциллограммы i(t) и U_c(t) на рис.5 при изменении параметров колебательного контура?

 

Список рекомендуемой литературы

Гинзбург С.Г. Методы решения задач по переходным процессам в электрических цепях. – М.:Высш.шк.,1967.-388 с.

Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. – М.: Высш.шк., 1981. – 334 с.

Поделиться:

Воспользуйтесь поиском по сайту: