 |
Используя формулу для максимальных касательных напряжений, можем записать условие прочности при кручении
|
|
|
|
Предел абсолютной упругости.
Предел пропорциональности.
Предел упругости.
Предел текучести.
20) Стержень с квадратным поперечным сечением нагружен силой F=1000kH. Модуль упругости материала E=200 Гпа. Допустимое напряжение (S)=100 Мпа. Допустимое минимальное перемещение верхнего сечения (S)=0,0001L. Допустимый размер поперечного сечения из условия жесткости равен 0,707 квадратных метров.

21) Допускаемое напряжение на растяжение – сжатие для материала равно 150 Мпа. Для стрежня круглого поперечного сечения наименьший диаметр D из условия прочности равен 0,0834 квадратных метров.
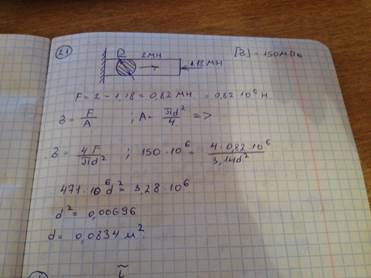
22) В чем разница между пластичными и хрупкими материалами? Образцы из хрупких материалов (например, из серого чугуна) разрушаются при весьма малых деформациях, а из пластичных материалов (например, из малоуглеродистой стали) - при значительных деформациях.
23) Что называется коэффициентом запаса прочности? Коэффициент запаса — величина, показывающая способность конструкции выдерживать прилагаемые к ней нагрузки выше расчётных. 
где S — предельно допустимое значение рассматриваемой величины (силы, напряжения, перемещения и т. д.);
T — расчетное значение этой величины.
24) Как формулируется условие прочности при любом виде де-формации?
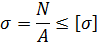
25) Что такое жесткость поперечного сечения? Жёсткость — это способность конструктивных элементов сопротивляться деформации при внешнем воздействии.
26) Что характеризует величина Е? Модуль упругости материала.
27) При расчете заклепки на срез величина площади среза равна
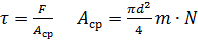 ; m=2
; m=2 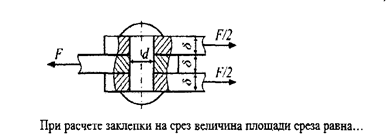
Ответ: 
28) Что называется абсолютным и относительным сдвигом?
Относительный сдвиг является угловой деформацией, характеризующей перекос элемента.
|
|
|
29) Как формулируется закон Гука при сдвиге?

30) Какова формула связи трех упругих констант (E, G и µ)?

31) Из расчета на срез минимальная высота головки болта при заданных значениях d и  равна
равна
При малой высоте головки болта происходит ее срез по цилиндрической поверхности диаметром d. Примем, что касательные напряжения постоянны по высоте h головки. 

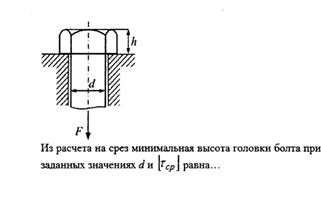
Ответ: h= 
32) При кручении максимальное касательное напряжение возникает в точке D 
Ответ: Точка D
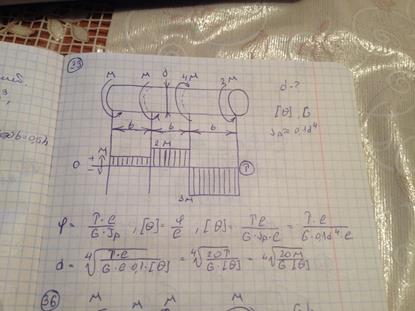
33) Из условия жесткости в заданных сечениях (а) и G, наименьший допускаемый диаметр вала равен
34) Труба испытывает деформацию кручение. Эпюра распределения касательных напряжений в поперечном сечении трубы имеет вид:

35) При деформации кручение угол взаимного поворота двух сечений, отнесенный к расстоянию между ними, называется относительным углом закручивания. 
36) Тогда максимальный угол закручивания равен:

37) Стержень круглого сечения диаметром d нагружен, как показано на рисунке. Максимальное значение угла закручивания равно
Модуль сдвига материала G, значение момента М и длина l заданы.
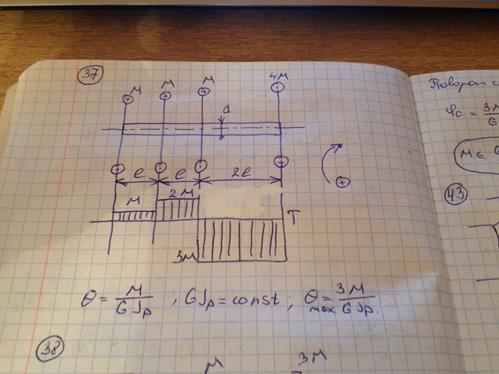
38) Схема нагружения показана на рисунке. Длина L, жесткость поперечного сечения стержня на кручение, допускаемый угол поворота сечения C заданы. Из расчета на жесткость максимально допустимое значение внешней нагрузки M равно (Эпюра наоборот, поменять плюс с минусом)


39) Правила построения эпюр крутящих моментов?
Правило знаков для Мкр: условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным - в противном случае.
40) Какие напряжения возникают в поперечном сечении круглого стержня при кручении и как они направлены?
В поперечных сечениях бруса при кручении возникают касательные напряжения, направление которых в каждой точке перпендикулярно к радиусу, соединяющему эту точку с центром сечения, а величина прямо пропорциональна расстоянию точки от центра.
|
|
|
41) Чему равен полярный момент инерции круглого сечения?

42) Что называется моментом сопротивления при кручении?
Полярный момент сопротивления  (или момент сопротивления при кручении), является геометрической характеристикой поперечного сечения вала, определяющей способность вала сопротивляться кручению. Полярный момент сопротивления измеряется в единицах длины в кубе (в см3).
(или момент сопротивления при кручении), является геометрической характеристикой поперечного сечения вала, определяющей способность вала сопротивляться кручению. Полярный момент сопротивления измеряется в единицах длины в кубе (в см3).
Для стержня круглого поперечного сечения полярный момент сопротивления определяется формулой:
 .
.
Для полого вала, имеющего внутренний диаметр d и внешний – D, полярный момент сопротивления выражается формулой:
 , где
, где  .
.
43) Максимальный относительный угол закручивания имеет место на участке номер 3. (исправить эпюру, все моменты вверху)

44) Условие прочности для стержня имеет вид:

45) Труба испытывает деформацию кручение. Касательное напряжение в точке C поперечного сечения трубы равно 20Мпа. Предел текучести материала трубы при чистом сдвиге  коэффициент запаса прочности
коэффициент запаса прочности  равен
равен


46) Что называется полным и относительным углом закручивания бруса? Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания.

47) Как производят расчет вала на прочность?
Используя формулу для максимальных касательных напряжений, можем записать условие прочности при кручении
 Wp – полярный момент сопротивления.
Wp – полярный момент сопротивления.
48) Как производят расчет вала на жесткость?
Условие жесткости требует, чтобы максимальный относительный угол закручивания θmax, вычисленный по формуле, был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

49) Статический момент площади сечения относительно оси x равен

50) Осевой момент инерции площади сечения относительно оси y равен

51) Для сечения известны осевые моменты инерции сечения относительно осей  ,
,  ,
,  :
:  ,
,  ,
, 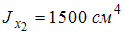 . Осевой момент инерции относительно оси
. Осевой момент инерции относительно оси  равен…
равен…

52) Что такое  и их единицы измерения?
и их единицы измерения?
1. Статический момент сечения, ед. измерения см^3;
|
|
|
2. Осевой момент инерции, ед. измерения см^4;
3. Полярный момент инерции, ед. измерения см^4;
4. Центробежный момент инерции, ед. измерения см^4.
53) Чему равен статический момент сечения относительно оси, проходящей через центр его тяжести? Равен нулю.
54) Формулы для определения осевых моментов инерции относительно центральных осей круга, прямоугольника, кольца?
1. Круг


2. Кольцо

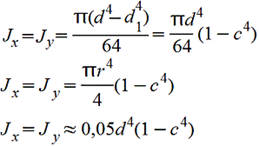
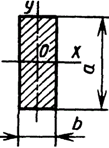
3. Прямоугольник

55) Если в плоскости сечения несколько параллельных осей, относительно какой из них  равен минимальному значению?
равен минимальному значению?
56) Что такое главные моменты инерции? Главными осями называются такие оси координат, относительно которых центробежный момент инерции равен нулю. Моменты инерции относительно главных осей инерции сечения называются главные моменты инерции сечения.
57) Осевой момент инерции сечения относительно оси х равен

58) Из указанных центральных осей главными осями сечения являются х3 и х1

59) Из указанных центральных осей сечения равнобокого уголка главными являются х3 и х1

60) Какие оси называются главными и главными центральными осями инерции? Главными осями называются такие оси координат, относительно которых центробежный момент инерции равен нулю. Главными центральными осями называются оси, проходящие через центр тяжести сечения.
61) Чему равен  относительно главных осей инерции? Равен нулю.
относительно главных осей инерции? Равен нулю.
62) В каких случаях без вычисления можно установить положение главных осей инерции сечения? Если фигура имеет ось симметрии.
63) Если 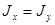 и
и 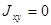 , то какие оси сечения являются главными?
, то какие оси сечения являются главными?
64) Ось, относительно которой статический момент площади сечения равен нулю, называется главной центральной осью.
65) Если 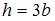 , то значение осевого момента инерции площади
, то значение осевого момента инерции площади

66) Статический момент площади сечения относительно оси x равен нулю.

67) Поперечное сечение балки составлено из вертикального листа и четырех неравнобоких уголков  . Характеристики уголка заданы. Размеры на рисунке даны в мм. Моменты инерции сечения
. Характеристики уголка заданы. Размеры на рисунке даны в мм. Моменты инерции сечения 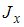 и
и  соответственно равны
соответственно равны
 8
8
68) Статический момент площади сечения относительно оси x равен…
|
|
|

69) Осевой момент инерции сечения относительно оси  равен
равен

70) Момент инерции площади фигуры относительно оси x, проходящей через центр тяжести фигуры, равен

71) На рисунке размеры поперечного сечения заданы в см. Осевой момент инерции сечения относительно центральной оси x равен

72) Поперечное сечение балки составлено из двух швеллеров №20 и листов, прикрепленных с помощью сварки. Характеристики швеллера приведены. Размеры на рисунке даны в мм. Осевой момент инерции сечения относительно главной центральной оси x равен

73) Момент инерции сечения относительно оси х равен, Координата центра тяжести 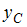 фигуры равна
фигуры равна

74) Зависимость между компонентами напряженного и деформированного состояния в пределах малых упругих деформаций имеет название обобщенного закона Гука.
75) Правило, согласно которому на взаимно перпендикулярных площадках элемента, выделенного из тела, касательные напряжения равны по величине и направлены к общему ребру (или от него), называют законом парности касательных напряжений.
76) Напряжение состояние «чистый сдвиг» показано на рисунке 3.

Решение:

Чистый сдвиг – напряженное состояние, когда на гранях выделенного элементарного объема действуют только касательные напряжения. Если элементарный объем повернуть на угол, равный  , то касательные напряжения на его гранях (площадках) будут равны нулю, но появятся нормальные (главные) напряжения
, то касательные напряжения на его гранях (площадках) будут равны нулю, но появятся нормальные (главные) напряжения 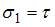 и
и  . Таким образом, чистый сдвиг может быть реализован растяжением и сжатием в двух взаимно перпендикулярных направлениях напряжениями, равными по абсолютной величине.
. Таким образом, чистый сдвиг может быть реализован растяжением и сжатием в двух взаимно перпендикулярных направлениях напряжениями, равными по абсолютной величине.
Следовательно, напряженное состояние «чистый сдвиг» показано на рисунке 3.
77) Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями.
78) На гранях элементарного объема (см. рисунок) определены значения напряжений в МПа. Угол между положительным направлением оси x и внешней нормалью к главной площадке, на которой действует минимальное главное напряжение, равен -22 градуса 30 минут.

79) Какие имеются виды напряженного состояния материала?

|
|
|


