 |
Блок-схема алгоритма метода дихотомии для решения нелинейных уравнений.
|
|
|
|
Составление нелинейных уравнений для поиска f0 и fпп по АЧХ для нагруженного LCR-ФНЧ 2 порядка.

Для определения  необходимо найти производную
необходимо найти производную  , т.к. в данной точке касательная параллельна оси X, тогда
, т.к. в данной точке касательная параллельна оси X, тогда
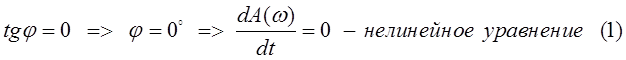
Для определения  необходимо найти точку перемещения графиков
необходимо найти точку перемещения графиков  и
и  , т.е.
, т.е. 
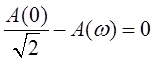 - нелинейное уравнение (2)
- нелинейное уравнение (2)
Решив эти уравнения найдем  и
и  , затем
, затем

Составление нелинейных уравнений для поиска f0 и fпп по АЧХ для нагруженного LCR-ФВЧ 2 порядка.

Для определения  необходимо найти производную
необходимо найти производную  , т.к. в данной точке касательная параллельна оси X, тогда
, т.к. в данной точке касательная параллельна оси X, тогда
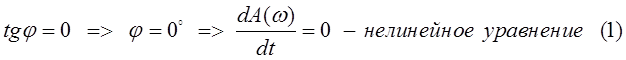
Для определения  необходимо найти точку перемещения графиков
необходимо найти точку перемещения графиков  и
и 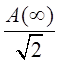 , т.е.
, т.е. 
 - нелинейное уравнение (2)
- нелинейное уравнение (2)
Согласно команде Mathcad  , тогда
, тогда 
Решив эти уравнения найдем  и
и  , затем
, затем 
Составление нелинейных уравнений для поиска f0 и fпп по ЛАЧХ для нагруженного LCR-ФНЧ 2 порядка.
 - проведем потенцирование функции по основанию 10.
- проведем потенцирование функции по основанию 10.
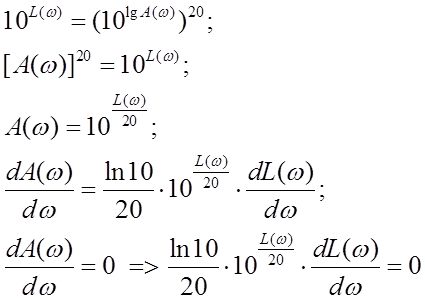
Таким образом, имея  можно найти
можно найти  , решив уравнение
, решив уравнение 

Найдем  : ЛАЧХ:
: ЛАЧХ: 
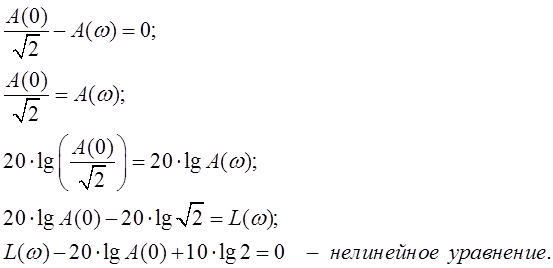
Решив это уравнение найдем  =>
=>  .
.
Составление нелинейных уравнений для поиска f0 и fпп по ЛАЧХ для нагруженного LCR-ФВЧ 2 порядка.
 - проведем потенцирование функции по основанию 10.
- проведем потенцирование функции по основанию 10.
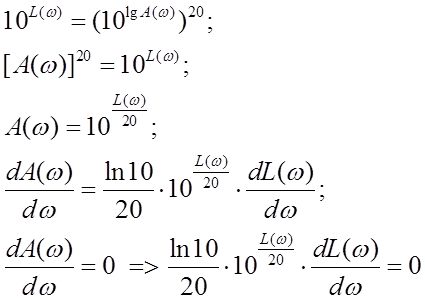
Таким образом, имея 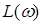 можно найти
можно найти 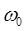 , решив уравнение
, решив уравнение 
 Найдем
Найдем  : ЛАЧХ:
: ЛАЧХ: 

Решив это уравнение найдем  =>
=>  .
.
Алгебраическая и показательная форма записи комплексной частотной характеристики. Пояснить на рисунке векторную форму комплексной частотной характеристики.
Операторной передаточной функцией ФВЧ  называется отношение изображение выходного сигнала
называется отношение изображение выходного сигнала  ко входному
ко входному  :
:

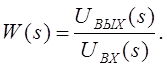 запишем выражение для операторной передаточной функции ФВЧ:
запишем выражение для операторной передаточной функции ФВЧ:

Заменим оператор Лапласа s на комплексную переменную j·ω: 
|
|
|


где  (25)
(25)
– вещественно-частотная характеристика (ВЧХ) ФВЧ,
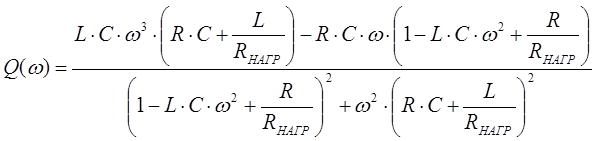 (26)
(26)
– мнимочастотная характеристика (МЧХ) ФВЧ,
 (27)
(27)
– амплитудно-частотная характеристика (АЧХ) ФВЧ,
 (28)
(28)
– фазочастотная характеристика (ФЧХ) ФВЧ.
Блок-схема алгоритма метода дихотомии для решения нелинейных уравнений.
Во многих научных и инженерных задачах возникает необходимость решения уравнений вида  где f – заданная функция;
где f – заданная функция;
x – неизвестная переменная; 
Считаем, что в уравнении (2.1) отделение корней проведено и на отрезке [a,b] расположен только один корень (рис. 2.2).

Суть метода дихотомии заключается в следующем [5].
Делят интервал [a,b] пополам и находят 
Корень будет находиться в той половине отрезка, на концах которой функция f (x) имеет разные знаки (в нашем случае это интервал 
Следовательно, для следующего шага уточнения корня точку b нужно переместить в середину отрезка, т.е. положить  , и продолжить процесс до тех пор, пока не будет выполняться условие
, и продолжить процесс до тех пор, пока не будет выполняться условие 
Следует учитывать, что вблизи корня значения  могут оказаться настолько малыми, что будут сравнимы с погрешностью вычисления. В этом случае говорят о попадании в так называемую полосу шума
могут оказаться настолько малыми, что будут сравнимы с погрешностью вычисления. В этом случае говорят о попадании в так называемую полосу шума 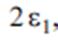 , которую следует задать, и прекратить процесс при попадании в нее.
, которую следует задать, и прекратить процесс при попадании в нее.
Заметим, что точка а всегда остается слева от корня, поэтому знак
функции в этой точке можно определять один раз и сравнивать знак функции в средней точке, т.е. знак  на совпадение или отличие от знака f (a).
на совпадение или отличие от знака f (a).
Алгоритм метода дихотомии приведен на рис. 2.3. Он состоит из
следующих этапов:
1. Ввод интервала [a,b], требуемой погрешности вычисления корня ε, полосы шума  .
.
2. Нахождение средней точки интервала: 
3. Проверка условия  и прекращение итерационного процесса (переход к п. 8) в случае его выполнения.
и прекращение итерационного процесса (переход к п. 8) в случае его выполнения.
4. Определение знака функции f (x) в средней точке  и в точке
и в точке  их сравнение.
их сравнение.
5. В случае совпадения знаков перенос точки a в точку  , в противном случае перенос точки b в точку
, в противном случае перенос точки b в точку 
|
|
|
6. Проверка условия (2.4) и прекращение итерационного процесса
(переход к п. 8) в случае его выполнения.
7. В противном случае возвращение к п. 2 и продолжение вычислений.
8. Вывод уточненного значения корня 
Преимуществами метода дихотомии являются его простота, надежность, сходимость к простому корню для любых, в т.ч. недифференцируемых функций [2]. К его недостаткам следует отнести относительно невысокую скорость сходимости и необходимость предварительного определения интервала, на котором функция меняет знак. Метод применяется главным
образом в тех случаях, когда требуется высокая надежность счета, а скорость сходимости малосущественна.
 |

|
|
|


