 |
Гладкая поверхность (без силы трения)
|
|
|
|
Реакция в зависимости от расположения точек касаний.
2)Гибкая связь. Реакция вдоль связи на растяжение.
3) Стержень. Реакция вдоль стержня и на растяжение и на сжатие.
4) Подшипник. Реакцию раскладывают по осям Х,Y. (неподв. опора, опора на катках)
5) Подпятник (петля двери)
Реакцию раскладывают по 3-м осям X,Y,Z.
5. Вращательным движением наз-ся такое движение, при котором остаются неподвижными точки, лежащие на оси вращения, а все остальные движутся по окружностям с центрами на этой оси.
характеристики: φ-угол поворота (в радианах), ω-угловая скорость (рад/с),
ε-угловое ускорение (рад/с2)
7.Равнодействующая система сходящ. сил определяется из условий равновесия системы схоящихся сил. Условия равнов. сходящихся сил: графически - Для геометрического равновесия необходимо, чтобы силовой многоугольник был замкнутым. аналитически -
RX = P1X + P2X + … +Pnx = Σ Pix
RY = P1Y + P2Y + … +PnY = Σ PiY
RZ = P1Z + P2Z + … +PnZ = Σ PiZ
R= 
8.Угловая скорость: 
= 
Частные случаи: 1) ε=0; ω=const;
2) ε ≠ 0, но ε=const; ω=ω0+εt
9.Связь называется идеальной, если возможная работа реакций связи = 0. В противном случае связь называется неидеальной. Пример идеальной связи: невесомый стержень, соединяющий 2 материальные точки М1 и М2. Их возможная работа = 0.
10. Условия равнов. сходящихся сил: графически - Для геометрического равновесия необходимо, чтобы силовой многоугольник был замкнутым. аналитически -
RX = P1X + P2X + … +Pnx = Σ Pix
RY = P1Y + P2Y + … +PnY = Σ PiY
RZ = P1Z + P2Z + … +PnZ = Σ PiZ
R=
12.Момент инерции тела относительно какой-либо оси наз-ся сумма произведений массы каждой точки на квадрат расстояния до оси. Момент инерции, относительно плоскости: JXOY = Σmizi2; JYOZ = Σmixi2;
|
|
|
JXOZ = Σmiyi2. Сумма 3-х этих уравнений даёт результат: JXOY + JYOZ + JXOZ = Σmi(xi2+ yi2+ zi2)
J0 = JXOY + JYOZ + JXOZ = ½* (JX + JY + JZ). Моменты инерции некоторых стандартных тел изображены на стенде. Центр масс, смещённых относительно оси вращения:
JZ = JC + md2 (
Штейнера)
13. 
Если свободное тело находится в равновесии под действием 3-х непараллельных сил, то линии действия этих сил пересекаются в 1-й точке.
14.Скорость 
; 
= 
15.Импульс тела (количество движения) -векторная физическая величина, равная произведению массы тела m на его 
, и направленная так же, как и скорость. Единица импульса тела - кг*м/с
Единица импульса силы – Н*с. Пусть скорость тела под действием силы F ⃗ изменяется за время Δ t от υ ⃗0 до υ ⃗. Согласно основному уравнению динамики F ⃗ = ma ⃗. Учитывая, что a ⃗ =(υ ⃗ − υ ⃗0)/ Δ t, получим F ⃗ Δ t = mυ ⃗ − mυ ⃗0⇒ F ⃗ Δ t = p ⃗ − p ⃗0 = Δ p ⃗ ⇒ Δ p ⃗ = F ⃗ Δ t. Формула выражает второй закон Ньютона, который может быть сформулирован следующим образом: изменение импульса тела равно импульсу равнодействующей сил, действующих на данное тело.
16. Пара сил – система 2-х параллельных равных по модулю и противоположенных по направлению сил. Пара сил не имеет равнодействующей (R=0) и не может быть уравновешена 1-й силой. Пара сил оказывает вращающее воздействие на тело (т.е. стремится его повернуть). Вращающее действие оценивается моментом пары = произведению силы на расстояние между линиями действия сил. (М=Р*h) H*m
17. Плоское (плоскопараллельное) движение – движение, при котором все точки тела движутся в плоскости, параллельной некоторой неподвижной плоскости. Это движение можно рассматривать, как сумму 2-х движений: поступательного, вместе с произвольной точкой (полюс) и вращательного движения вокруг полюса, при этом поступательное движение зависит от выбора полюса, а угол поворота и направление поворота не зависят от выбора полюса.
|
|
|
– 
Скорость любой точки (плоской фигуры) = геометрической сумме полюса + вращательная этой точки, относительно полюса.
18.Центр масс – точка, координаты которой определяются: 
; 
;
геометрически центр тяжести и центр масс – одна и та же точка.
19.Чтобы найти момент силы, относительно оси, нужно спроецировать эту силу на плоскость, перпендикулярную оси и найти момент этой проекции относительно точки пересечения плоскости и оси.
20. Скорость любой точки (плоской фигуры) = геометрической сумме полюса + вращательная этой точки, относительно полюса.
21. Пара сил – система 2-х параллельных равных по модулю и противоположенных по направлению сил. Пара сил не имеет равнодействующей (R=0) и не может быть уравновешена 1-й силой. Пара сил оказывает вращающее воздействие на тело (т.е. стремится его повернуть). Вращающее действие оценивается моментом пары = произведению силы на расстояние между линиями действия сил. (М=Р*h) H*m.
22.Плоскую систему произвольно расположенных сил можно заменить системой сходящихся сил, приложенных в центре приведения, добавив при этом систему пар сил, с моментами, равными моментам сил, относительно центра приведения. (согласно правилу Пуансо)
ΣPiX = 0
ΣPiY = 0
ΣMPi (отн. точки О) = 0
На рисунке преобразована только сила Р1. По её аналогии преобразовать остальные силы.
23.Мгновенный центр скоростей – точка, 
которой в данный момент времени = 0.
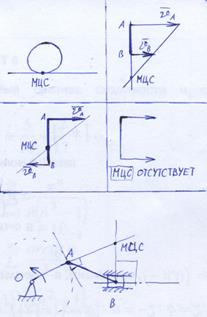
24.Момент инерции тела относительно какой-либо оси наз-ся сумма произведений массы каждой точки на квадрат расстояния до оси. Момент инерции, относительно плоскости: JXOY = Σmizi2; JYOZ = Σmixi2;
JXOZ = Σmiyi2. Сумма 3-х этих уравнений даёт результат: JXOY + JYOZ + JXOZ = Σmi(xi2+ yi2+ zi2)
J0 = JXOY + JYOZ + JXOZ = ½* (JX + JY + JZ). Моменты инерции некоторых стандартных тел изображены на стенде. Центр масс, смещённых относительно оси вращения:
JZ = JC + md2 ( Штейнера)
Примечание: - означает теорема.
Отсутствуют ответы на 3, 6, 11, 25 вопросы
44. Динамикой называется раздел механики, в котором изучается движение материальных тел в зависимости от действующих на них сил.
|
|
|
Основные законы динамики:
1) Закон инерции: материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит это состояние.
2) Закон пропорциональности силы и ускорения: ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление.
3) Закон равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие.
4) Закон независимости действия сил: несколько одновременно действующих на материальную точку сил сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их геометрической сумме.
30. Принцип Германа – Эйлера – Даламбера называют общий метод, с помощью которого уравнениям динамики по форме придается вид уравнений статики.
Предположим, что материальная точка М под действием системы сил Р1, Р2, …, Рn движется с ускорением а (рис)
Основное уравнение динамики имеет вид:
ma=P1+P2+…+Pn
Перенесем член ma из левой части уравнения в правую:
0=P1+P2+…+Pn –ma.
Так как –ma =Ф, то
P1+P2+…+Pn+Ф=0.
Полученное соотношение формулируется так: геометрическая сумма всех приложенных к точке сил и силы инерции этой точки равны нулю.
Как известно, в действительности сила инерции материальной точки приложена не к ней, а к телу, сообщающему точке ускорение.
Приложенные силы инерции к точке являются лишь условным приемом, сводящим задачу динамики по форме решения к задаче статики.
Благодаря простоте этот метод получил широкое применение во многих прикладных дисциплинах. В ряде случаев он обеспечивает наиболее простое и удобное решение задач динамики.
35. Кориолисовым ускорением называется составляющая абсолютного ускорения точки в сложном движении, равная удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки: ac=2(we*vr).
Кориолисово ускорение характеризует:
1) изменение модуля и направления переносной скорости точки вследствие её относительного движения;
|
|
|
2) изменение направления относительной скорости точки вследствие вращательного переносного движения.
Модуль кориолисова ускорения определяется как модуль векторного произведения:
ac=2wevr sin(we, vr).
Для определения направления кореолисова ускорения используют правило Жуковского: чтобы найти направление кориолисова ускорения, следует спроецировать относительную скорость точки на плоскость, перпендикулярную оси переносного вращения, и повернуть эту проекцию в той же плоскости на 90 градусов в сторону переносного вращения.
47. Динамикой называется раздел механики, в котором изучается движение материальных тел в зависимости от действующих на них сил.
Задачи динамики: 1) по известному закону движения определить действующие силы; 2) (обратная задача динамики) – по известным силам определить закон движения.
48. Телом переменной массы называют тело, масса которого изменяется с течением времени.
Уравнение движения представляет собой основное уравнение динамики точки переменной массы и называется уравнением Мещерского.
Из этого уравнения следует, что уравнение движения точки переменной массы имеет вид основного уравнения динамики точки постоянной массы, находящейся под действием приложенных к ней сил и реактивной силы: d(mv)/dt=P, ma=F+Fр.
27. Теорема Штейнера: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела (m) на квадрат расстояния (d) между осями: J=Jc+md квадрат, где Jc – известный момент инерции относительно оси, проходящей через центр масс тела, J – искомый момент инерции относительно параллельной оси, m – масса тела, d – расстояние между указанными осями.
40. Рычагом называется твердое тело, имеющее неподвижную ось вращения и находящееся под действием сил, лежащих в плоскости, перпендикулярной этой оси.
Рычаг находится в равновесии тогда, когда сумма моментов сил, вращающих его по часовой стрелке, равна сумме моментов сил вращающих его против часовой стрелки. В простейшем случае для двух сил F1d1=F2d2, или силы обратно пропорциональные длинам плеч (F1/F2=d2/d1).
39. Количеством движения материальной точки называется вектор, имеющий направление вектора скорости, и модуль, равный произведению массы точки (m) на модуль скорости её движения (v).
34. Статически определимыми называют задачи, которые можно решать методами статики твердого тела, т. е. задачи, в которых число неизвестных не превышает числа уравнений равновесия сил. Статически неопределимыми называют задачи с числом неизвестных, превышающим число уравнений равновесия сил, т. е. задачи, которые нельзя решать методами статики твердого тела и для решения которых нужно учитывать деформации тела, обусловленные внешними нагрузками.
|
|
|
26. Ускорения точек плоской фигуры определяется следующей теоремой: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки в её вращении вместе с плоской фигурой вокруг полюса.
29. Вынужденные колебания – колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Вынужденные колебания совершает материальная точка, на которую наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая возмущающей силой.
29. Вынужденные колебания – колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Вынужденные колебания совершает материальная точка, на которую наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая возмущающей силой.
- уравнение движения.
36. Количеством движения материальной точки называется вектор, имеющий направление вектора скорости, и модуль, равный произведению массы точки (m) на модуль скорости её движения (v).
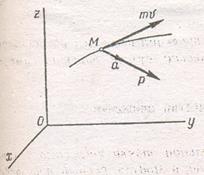
Теорема об изменении количества движения материальной точки: производная по времени от количества движения материальной точки геометрически равна равнодействующей сил, приложенных к той точке.
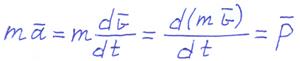
37. Определение усилий в стержнях ферм по способу Риттера.
Применим метод сечений к определению усилий в стержнях плоских ферм. На ферму действуют вертикальные внешние силы: задаваемая сила P=60 кН и реакции опор
RA=40 кН и RB=20 кН.
При определении усилий все стержни фермы условимся считать растянутыми, знак минус в ответе будет означать, что стержень сжат, Пусть требуется определить усилие в стержне 6 фермы. Для этого проводим сечение I – I, рассекая не более трех стержней, в том числе стержень 6, усилие в котором определяется. Мысленно отбрасываем левую часть фермы, заменяя её действие на оставшуюся правую часть усилиями S6, S7 и S8, приложенными в соответствующих сечениях стержней и направленными в сторону отброшенной части. Чтобы определить усилие S6 независимо от усилий S7 и S8, составляем уравнение моментов сил, действующих на правую часть фермы, относительно точки K, в которой пересекаются линии действия сил S7 и S8. Эту точку называют точкой Риттера:
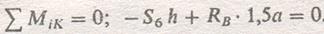
Так как h=0,5a, то S6=RB*1,5a/(0,5a)=60 кН.
Воспользуемся тем же сечением I – I для определения усилия S7 независимо от усилий S6 и S8. Спроецируем все силы, действующие на правую часть фермы, на вертикальную ось у, так как проекции сил S6 и S8 на эту ось равны нулю:
Для определения усилия S8 составим уравнение моментов этих же сил относительно точки Риттера L, а которой пересекаются линии действия сил S6 и S7:
Знаки полученных ответов показывают, что стержень 6 растянут, а стержни 7 и 8 сжаты.
Изложенный способ определения усилий в стержнях фермы предложен Риттером и носит название способ Риттера.
|
|
|
